Statistical Method for Development of Composite Index in Clinical Research

Introduction

In clinical research, a medical predictive model is often established using a multivariate set of risk factors (predictors). The purpose of a medical predictive model is not only to predict the performance of clinical outcome but also to provide valuable information regarding disease management including prevention, accurate and reliable diagnosis, and effective treatment of the diseases under study. In practice, for building a medical predictive model with a multivariate set of risk factors, a (logistic) regression analysis approach is often performed by the following steps: (i) identifying potential risk factors (e.g., demographics or patient characteristics) by determining associations between the potential risk factors and the response, (ii) testing for co-linearity among the identified risk factors, (iii) performing predictive model fitting with the identified predictors, (iv) performing goodness-of-fit of the fitted model, and (v) validating the developed medical predictive model [1]. In addition, generalizability of the medical predictive model should be examined for the purpose of external validation.

A well-established and validated medical predictive model upholds sparse predictors, particularly when these predictors are highly correlated with (dependent on) one another. Therefore, the principle investigator will try to integrate multiple predictors into a single predictor that informs the disease status and/or treatment effect while upholding accuracy and reliability [2]. Since each of the multiple predictors may be positively or negatively and/or linearly or nonlinearly correlated to the clinical outcome or response, an ideal composite index should be able to account for positive/negative and/or linear/non-linear associations with the clinical outcome.

Similar to statistical methods used for characterizing calibration (standard) curves in lab-based assays, we will develop an ideal composite index using similar criteria and corresponding methods. For example, we propose that an ideal composite index should be of the format: x₁^a x₂^b , where x₁ and x₂ are identified, highly correlated risk factors/predictors. Next, a procedure for the development of the ideal composite index, based on a multiple regression analysis model, is proposed. Under the multiple regression analysis model, statistical methods are derived accordingly. The criteria, process, and statistical methods are evaluated both theoretically and via a simulation study.

The remainder of this article is organized as follows: Section 2 will briefly introduce the concept of an ideal composite index, using examples from existing clinical research, and propose an innovative procedure for the development of an ideal composite index in clinical research; Section 3 will derive the statistical methods; Section 4 will apply the proposed to composite index in a simulation study.

Development of a Composite Index

Under a well-established medical predictive model, it is common to see that these predictors may be dependent on, or somehow correlated to one another in a linear/nonlinear and/or positive/ negative fashion.

Ideal Composite Index

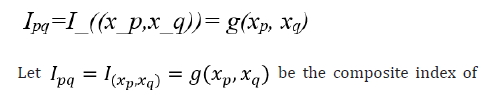
x_p and x_q , where x_p and x_q are identified and highly correlated predictors which are relevant to clinical outcome and g is a utility function that combines x_p and x_q . The goal of the ideal composite index is to identify the utility function g such that the developed index can account for positive/negative and/or linear/non-linear associations between each of the predictors (i.e., x_p and x_q ) and the clinical outcome.

practice, the selection of function g depends upon the relationship between the clinical outcome and each of the predictors (i.e., x_p and x_q ). For this purpose, we may consider the selection of a standard curve or calibration curve in the development and validation of an analytical method in laboratory testing. Let y be the amount of drug recovered (% of label claim) and x be the standard concentration. A standard curve or calibration curve is often determined based on the model fitting between y_i and x_i where i=1,..,n. In assay development and validation, the following four models are commonly considered:

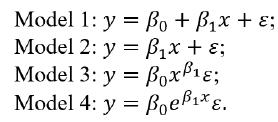
Model 1 is linear with a non-zero intercept, while Model 2 is linear without an intercept. Model 3 and Model 4 are non-linear but can be linearized by taking the logarithm. Based on the consideration that an ideal composite index should be able to account for positive/negative and/or linear/non-linear associations between each of the predictors (i.e., x_q ) and the clinical outcome (y), we propose selecting the utility function g as follows

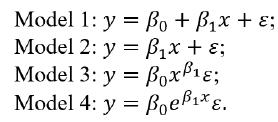
Model 1 is linear with a non-zero intercept, while Model 2 is linear without an intercept. Model 3 and Model 4 are non-linear but can be linearized by taking the logarithm. Based on the consideration that an ideal composite index should be able to account for positive/negative and/or linear/non-linear associations between each of the predictors (i.e., x_q ) and the clinical outcome (y), we propose selecting the utility function g as follows

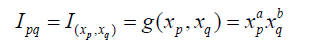
Example 1 – In clinical research, the above proposed composite index is commonly seen in practice. A typical example is the development of body mass index (BMI). As indicated in BMI [3], the BMI was first discussed by Quetelet in his published research work on the weight of men at different ages in 1832. BMI serves as a medical predictive model for obesity, and uses the two predictors of x_p =

The scaling factor of 1.3 was determined to make the new BMI formula align with the traditional BMI formula for adults of average height. The exponent of 2.5 is a compromise between the exponent of 2 in the traditional formula for BMI and the exponent of 3 that would be expected for the scaling of weight with height.

Example 2 – Consider QT interval prolongation for cardiotoxicity Let x_p = QT interval and x_q = heart rate (RR). Bazett [5] and Fridericia [6] proposed the following indices, which is a corrected QT interval (denoted by QTc ) adjusted for the square root of RR, respectively:

Proposal for Development of a Composite Index

In the interest of minimizing predictors, especially when these predictors are dependent on one another, and upholding generality, we consider the development of a composite index based on two confirmed predictors x_p and x_q, which are corrected for each other. We propose the following steps for the development of an ideal composite index by reducing a two-parameter ( x_p and x_q ) problem to a single parameter (the composite index) problem.

Step 1. Establish and validate a medical predictive model. Let y denote the clinical outcome/response (independent variable) and

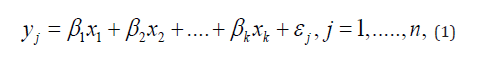
where β_i,I = 1,....kare regression coefficients and i ε is the random error term. Under the multiple regression model, a (logistic) regression analysis approach is often performed to (i) identify potential risk factors/predictors (e.g., demographics or patient characteristics) by determining associations between the potential risk factors/predictors and the response, (ii) test for collinearity among the identified risk factors/predictors, (iii) build a medical predictive model by fitting the clinical outcome/response with the identified predictors, (iv) perform goodness-of-fit of the fitted model, and (v) validate the developed medical predictive model based on some pre-specified performance criteria.

Step 2. Under the established and validated medical predictive model, obtain estimates of the regression coefficients of the two predictors x_p and x_q, which we will develop into a composite index accordingly.

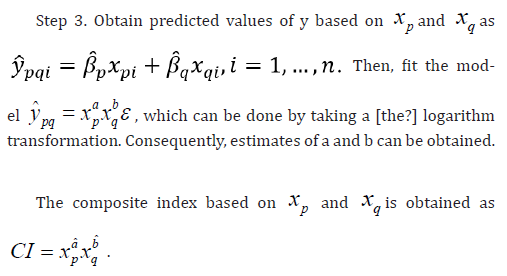
Statistical Method

Obtain Estimates of Regression Coefficients of Predictors

Under Model (1). Without loss of generality, assume y and all

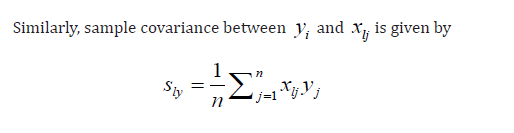
As a result, sample correlation between x_p and x_q and y are given by respectively.

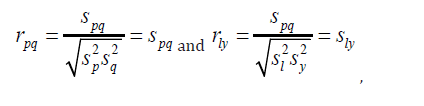
In order to obtain estimates of β_p and β_q , consider rewriting model (1) in the following matrix form

Y = Xβ +ε (2)

where Y is the nx1 vector of dependent variables, X is the nxK matrix of regressors, β is the Kx1 vector of regression coefficients, and ε is the nx1 vector of random error terms. Under model (2), the ordinary least squares (OLS) estimator of β is given by

Fitting the Model between Predicted Values and the Composite Index

For the development of the composite index based on x_p and x_q, which are dependent on each other,

consider fitting the following multicaptive model between the predicted values

Validation of the Developed Composite Index

where p₀ is some pre-specified constant. If the conclusion is to reject H₀ in favor H_a , then the developed composite index is considered validated. The technical details of the test of hypothesis corresponding to the two criteria can be found in Tse et al. [7].

Simulation Study

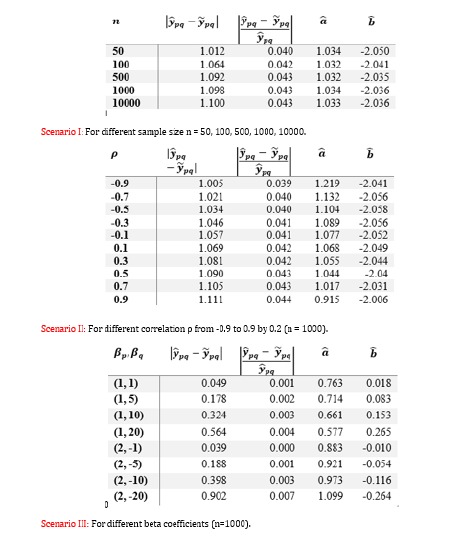
In the simulation study, we construct a composite index that follows the similar modelling of body mass index with randomly generated weight x_p and x_q data. We examine three scenarios at which predictive accuracy could be affected. Firstly, we run the simulation for different sample sizes and compare the closeness of developed composite index to the observed value. Secondly, we analyse whether the correlation relationship between the predictors will affect the predictive accuracy. Thirdly, we test under different regression equations for observed y_i and x_i , the estimation of

Figure 1: Evaluation of the Closeness between y_pq-y_pq

As shown in Table 1, the estimation of the proposed composite index is not affected by the sample size. Even for small sample size such as n = 50, the estimation is accurate and consistent. In scenario II, the difference between y_pq-y_pq is minor for proposed correlation between x_p and x_q With higher correlation coefficient, the difference becomes relatively smaller. For different beta coefficients, the relative difference is robust while the absolute difference has a minor trend of increase when response variable increases. Our results suggest the need to scale the risk factors or leave aside the intercept term before applying the linear regression model for the log-transformed variables.

Concluding Remarks

In this article, although the development of the composite index focuses on two dependent predictors, similar idea can be easily extended to develop a composite index combining more than two predictors, which are correlated one another. In the multiple regression analysis, the ordinary least squares (OLS) approach is considered for obtaining the estimates of regression coefficients. In practice, alternatively, we may consider weighted OLS (WOLS) for adjustment if heterogeneity in predictors are present.

An ideal composite index should possess the following advantages. First, in the interest of parsimony of predictors, the development a composite index reduces a multiple-parameter (e.g., two predictors as discussed in this article) problem to a single parameter (the developed composite index) problem. Second, the developed composite index is able to address the positively/negatively and/or linearly/non-linearly correlation between each of the two predictors (which are correlated each other) and the response. Third, the developed composite index outperforms each individual predictor in two ways: (i) if each predictor can inform the disease status or treatment effect, the composite index can definitely do and (ii) if the composite index can inform the disease status or treatment effect, each individual predictor may not be able to.

A future possibility is to build and check the quality of a composite index containing a variable for body structure and a variable for muscle mass, especially since risk for diabetes can be influenced by relative muscle mass for people with same height and weight, thus same BMI. In addition to body frame, such as large or small, despite same height could also be taken into account.