Dissociation Energy of an (O₂) Oxygen Molecule by DFT Calculations

Introduction

The aim of this work is the breakdown of the O₂ molecule from a platinum catalyst (Pt), a platinum surface (Pt₄) and a catalytic support (C₆₀Pt₄) using DFT calculations. For cancer therapy in the late 1970s, cisplatin has been used so widely that it is often called ‘‘penicillin of cancer’’. The continued success of this chemotherapeutic drug inspired the further development of platinum compounds for anticancer therapy, generating hundreds of cisplatin analogs. Nevertheless, platinum complexes are promising anticancer agents, as they show high stability and bioavailability, allowing oral application and overcoming side effects such as nephrotoxicity [1,2]. Platinum complexes must be activated by reduction to release their active platinum metabolites. Therefore, platinum complexes, as bioreductive prodrugs, might target hypoxia and close the gap between classic metal-based and targeted therapies [3,4]. Moreover, platinum complexes can be used to build new carboplatin molecules against hypoxia. As an example, carboplatin-loaded chitosan nanoparticles (CRB NP) have been proposed to increase the cancer treatment efficiency in wilm’s tumor [5]. In addition, the platinum (supported by high-surface area carbons, i.e. Pt/C) is employed as the main electrocatalyst material in both anode and cathode [6] where there are reaction mechanisms between the Pt catalyst and one of the fuels (O₂), and for a good reason platinum is the best single element catalyst in acidic media for the hydrogen oxidation reaction (HER) and the oxygen reduction reaction (ORR) taking place on the two electrodes, respectively [7,8]. The widespread application of platinum in electrocatalysis is due to its relatively good stability [9,10] on fuel cells of PEM kind. Previously, preliminary ab initio calculations on the Pt(³D,¹S)-O₂ interaction have been accomplished [11]. The reason we need for calculating over and over the Pt-O₂ interaction thus studied is that we need to understand more clearly the most part of its reaction mechanisms. This is pursued with the intention to design fuel cells among other applications [12]. DFT theoretical calculations provide useful information for designing processes of fuel transformation in the fuel cells.

Computational Method

In this work, DFT calculations are achieved through Biovia Materials Studio Dmol3 software [13,14] The exchange and correlation function are applied using the generalized gradient approximations (GGA), and Perdew Burke and Ernzerhof (PBE) [15] functional, which provides good results, with a set of double bases (dnd). The set of bases have the advantage of being equivalent to the Gaussian base 6-31G* for restricted spin [16]. All structures were optimized until the forces were less than 0.002 Ha / Å. DMol³ module is used to calculate total energy, where energies are obtained by single point calculations with Hartree-Fock method [16]. Connectivity calculation of BIOVIA Materials Studio DMol3 on no-bonding to s- and f-shell scheme, bond type, and converting representation to Kekulé, for bond length tolerances from 0.6 to 1.15 Å is a software-tool to bond atoms according to their separation distance, which has been applied for building possible reactivity products [17].

Results and Discussion

Interaction of the Platinum atom with an Oxygen atom (Pt-O)

It was considered to carry out the Pt-O interaction as input in the simulation as shown in Figure 1 where a starting distance of 3.16 Å has been proposed to start with geometry optimization calculation.

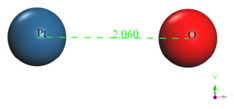
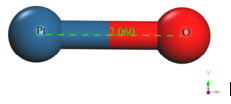
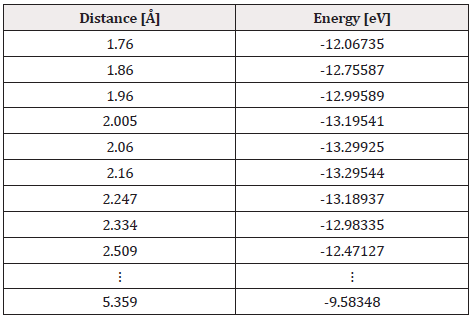
The output result of the geometry optimization produced an equilibrium distance of 2.06 Å (Figure 2) and an equilibrium energy of -13.2992 eV.

The connectivity calculation was carried out and we got the corresponding bond as shown in Figure 3.

Figure 1: Molecular arrangement of the platinum atom with the oxygen atom (input).

Figure 2: Geometry optimization of the molecular arrangement (output).

Figure 3: Connectivity calculation for bonding this molecular arrangement.

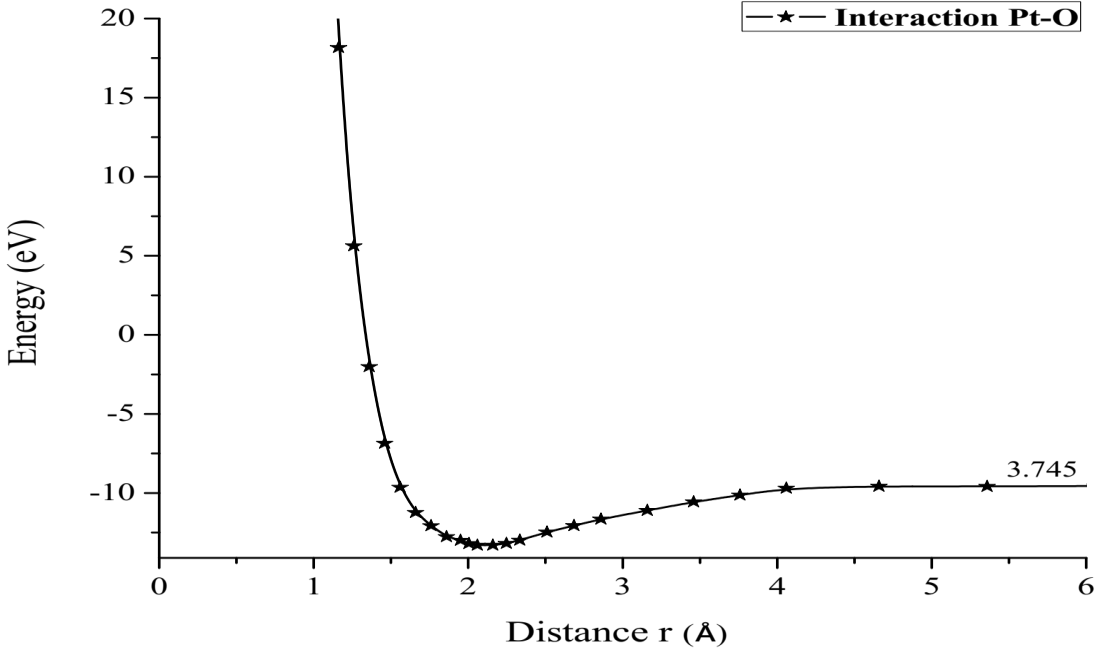
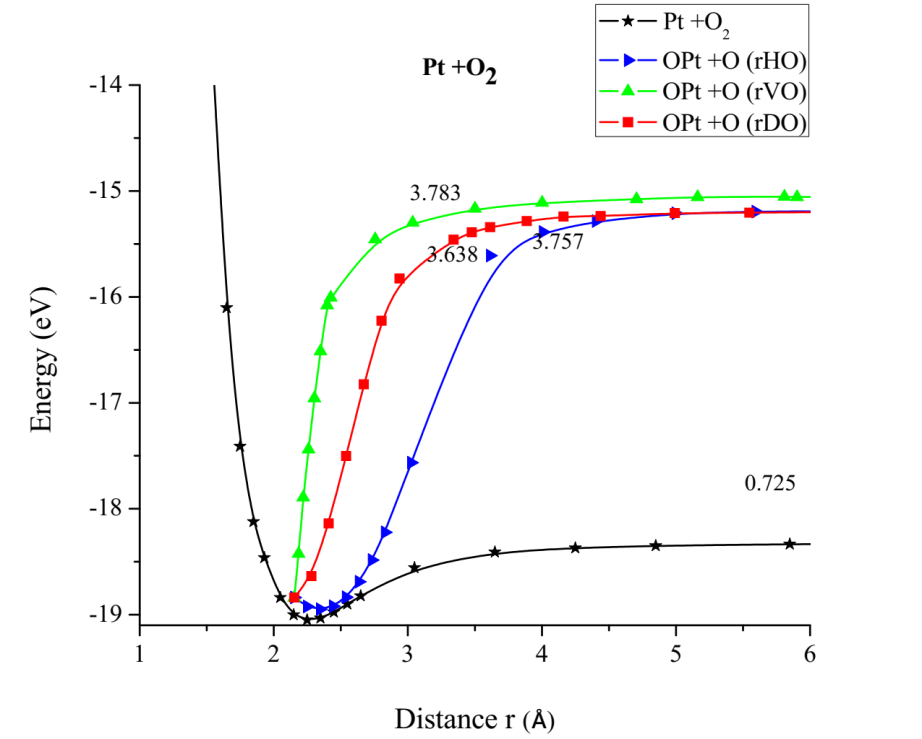
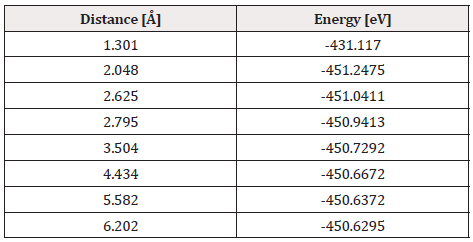
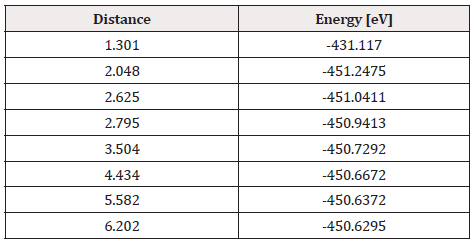
Once the distance and equilibrium energy were obtained, one of the two atoms was fixed, in this case it was the platinum atom, the oxygen atom moved away step by step with each step of 0.1Å until reaching a constant energy at an infinite separation distance, at each position of the oxygen atom its energy is calculated, and thus we construct the curve of the potential energy well. Table 1 exhibits distances and energies obtained for the construction of the potential energy well, which is 3.745eV size as shown in Figure 4.

Comparing the energy of the potential well of the Pt-O interaction, which is 3.745eV in our simulation, and the experimental value of 3.82eV [18] there is an error of 1.4%.

Figure 4: Connectivity calculation for bonding this molecular arrangement.

Table 1: Distances and Energies of the Pt-O Interaction.

Interaction of the Platinum atom with an Oxygen molecule (Pt-O₂)

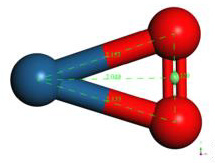
The geometry optimization of the oxygen molecule (O₂) calculation, with an O = O bond distance of 1.21Å in the simulation, has been compared with an experimental value of 1.25Å [18] as shown in Figure 5.

The geometry optimization calculation of platinum atom with oxygen molecule provides the equilibrium energy, and at the input, the platinum atom is placed at a separation distance of 3.5Å from the oxygen molecule, to carry out the calculation (Figure 6).

Geometry optimization gives an equilibrium distance of 2.049Å and an equilibrium energy of -18.838 eV. The connectivity calculation was accomplished (Figure 7).

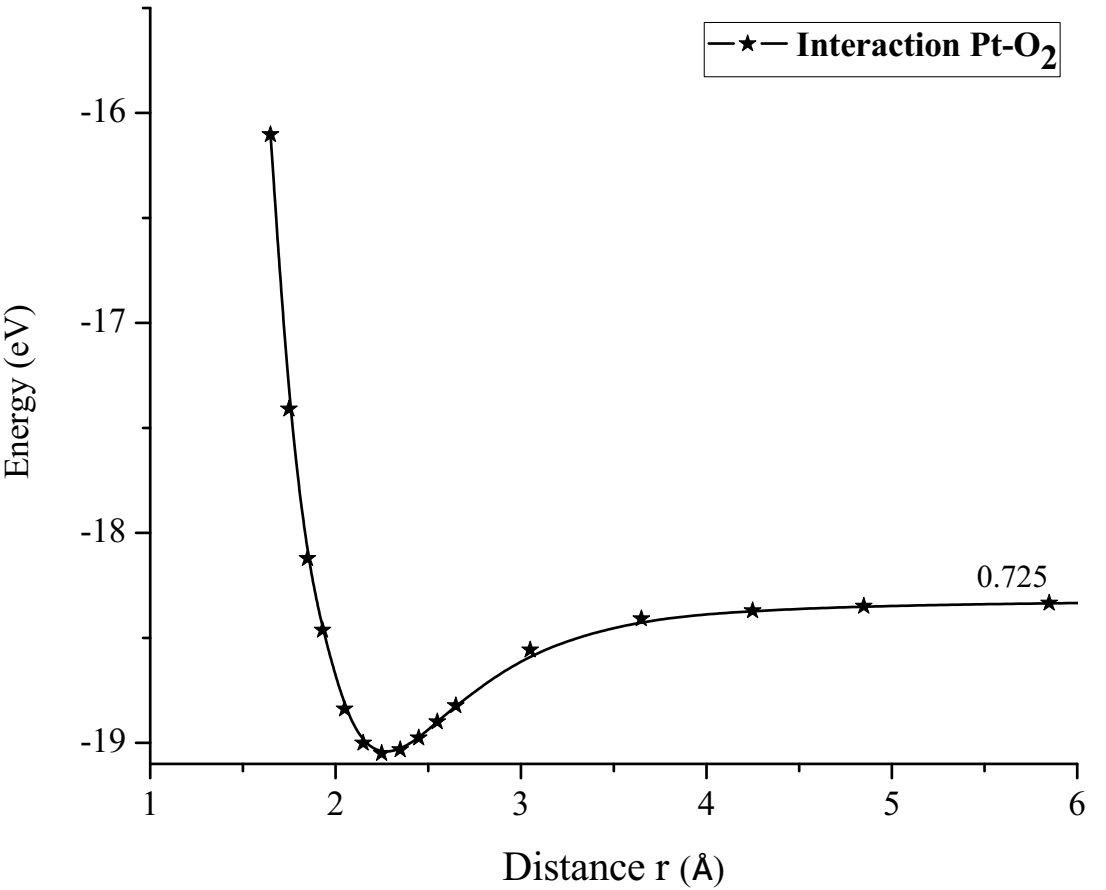
The potential energy well of the Pt-O₂ interaction is calculated as shown in Figure 8. Where the platinum atom is fixed, and the oxygen molecule is moved away and closer from 0.1Å to 0.1Å. At each distance, an energy value is obtained as shown in Table 2, for which a potential well size of 0.725eV has been determined. The experimental value of this interaction is equivalent to 0.719eV [19]. Then, the approximation error is 1% between the calculated and experimental value (Figure 8).

The PtO₂ intermediate complex is taken to break an oxygen atom and free it with PtO + O products. Table 2 of the potential energy of PtO₂ has an equilibrium distance of 2.049Å, an equilibrium energy -18.838eV, and a potential energy well depth 0.725eV. Previous equilibrium distance is shown in Figure 7, which also exhibits 1.32Å for O-O bond length, and it must be noticed that the well depth value agrees with the energy obtained by a fuel mono cell [20-22].

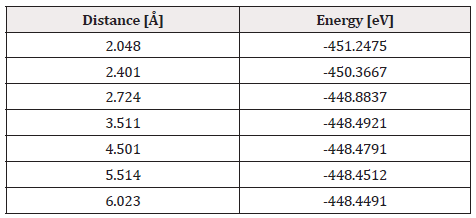
From the already optimized system we fixed two atoms, the platinum atom, and the oxygen atom, later an oxygen atom is moved away due to it is not fixed. It is moved horizontally until the energy is constant. For each distance, an energy value is obtained as shown in Table 3 (Figure 8).

The potential energy curve is constructed, and the well size is found to be 3.646eV (Figure 10). This agrees with potential energy well depth of the Pt-O interaction calculated previously (Table 3).

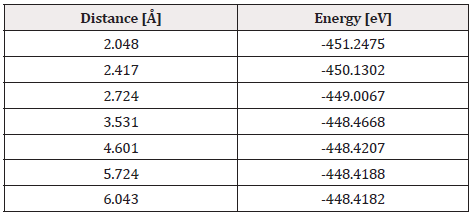
The already optimized Pt + O₂ system was taken up again now as PtO₂, then fixing two atoms, one of platinum and one of oxygen, later an oxygen atom that is not fixed is vertically moved away step by step until the energy is constant. For each distance, an energy value is obtained as shown in Table 4 (Figure 11&12).

Figure 5: Optimized oxygen molecule.

Figure 6: Molecular arrangement of the platinum atom with the oxygen molecule (input).

Figure 7: Geometry optimization of the Pt-O2 molecular arrangement.

Figure 8: Potential energy curve of the Pt-O2 interaction.

Figure 9: a) Moving the oxygen atom away horizontally, b) Breaking one of the Pt-O bonds.

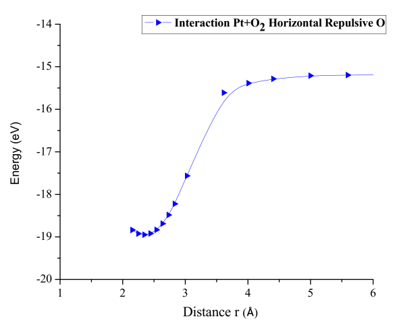
Figure 10: Potential energy curve of the breaking of the Pt-O bond, moving the oxygen atom away horizontally.

Figure 11: a) Moving the oxygen atom away vertically, b) Breaking one of the Pt-O bonds.

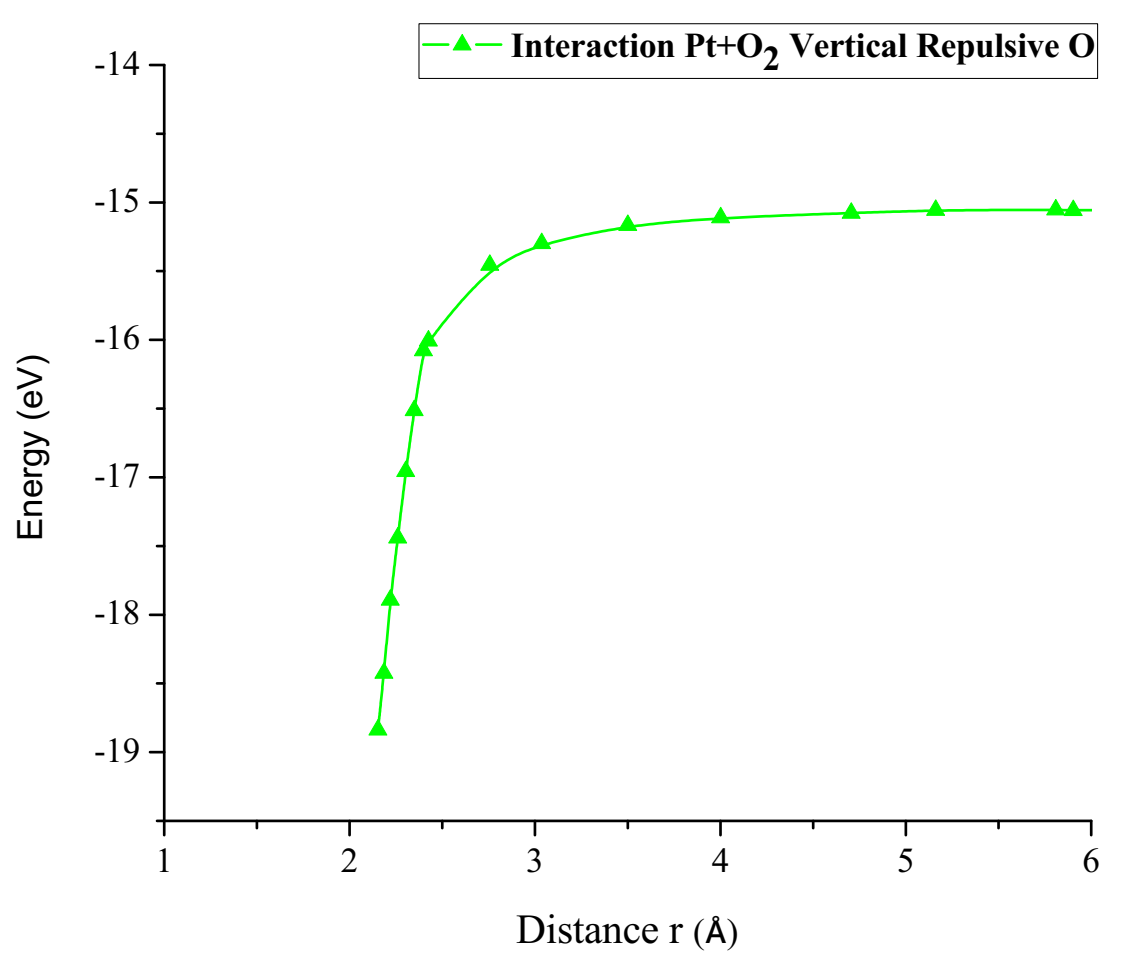
Figure 12: Potential energy curve of the breaking of the Pt-O bond, moving the oxygen atom away vertically.

Table 2: Distances and Energies of the Pt-O2 Interaction.

Table 3: Distances and Energies of the Pt-O2 Interaction (Horizontal).

Table 4: Distances and Energies of the Pt-O2 Interaction (Vertical).

The energy curve for breaking the O₂ molecule was constructed vertically, it was found that potential well size is 3.783eV as shown in Figure 12. This agrees with potential energy well depth of the Pt-O interaction calculated previously.

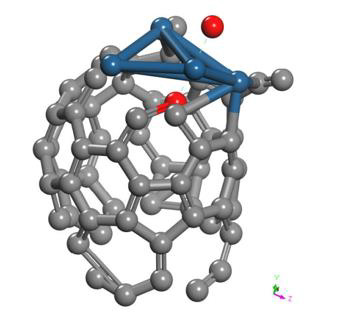
Finally, the optimized Pt + O₂ system is taken again, by fixing platinum and oxygen atoms, and the other oxygen atom is moved away diagonally until the energy calculated is constant (Figure 13). For each distance, an energy value is obtained as shown in Table 5.

The energy curve for breaking the O₂ molecule is now constructed diagonally, and the well size is 3.638eV (Figure 14). Which agrees with the previous potential energy well depth of Pt-O interaction calculated (Table 5).

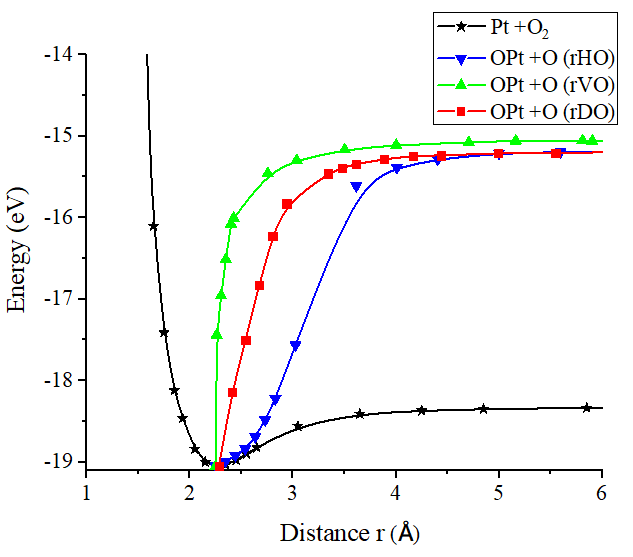
In Figure 15 it is found that the inflection points, vertical repulsive oxygen (vrH) = 3.783Å, diagonal repulsive oxygen (drH) = 3.638Å, horizontal repulsive hydrogen (hrH) = 3.757Å, consequently it is found that drH breaks before hrH and this before vrH. And with energies vrH = 3.783eV, drH = 3.638eV, hrH = 3.757eV, these correspond to what it takes on average almost the same amount of energy to dissociate a Pt-O bond. This agrees with potential energy well depth of the Pt-O interaction calculated previously.

Figure 13: a) Diagonally moving the oxygen atom away, b) Breaking of one of the Pt-O bonds.

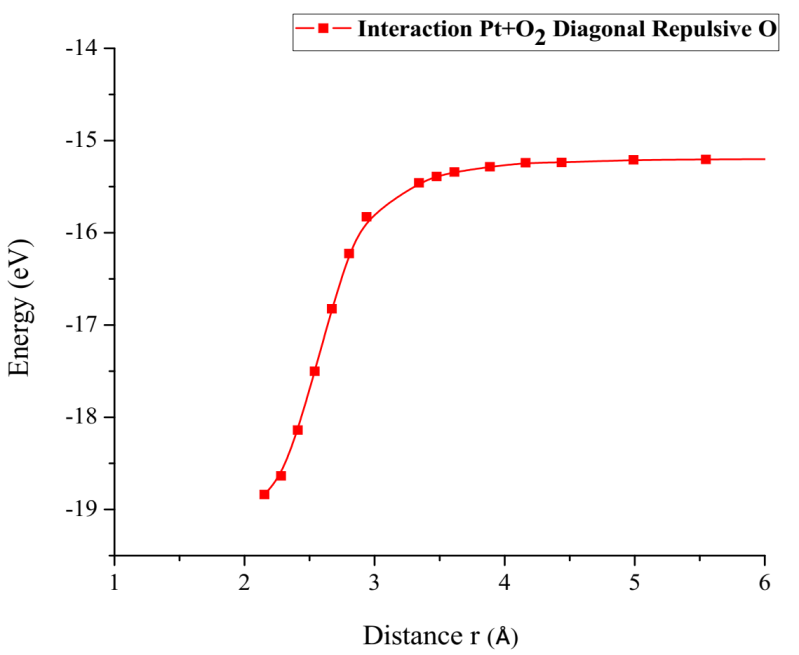
Figure 14: Potential energy curve of the breaking of the Pt-O bond, moving the oxygen atom away vertically.

Figure 15: Comparison of Interactions.

Table 5: Distances and Energies of the Pt-O₂ Interaction (Diagonal).

Interaction of a Platinum Cluster with an Oxygen molecule (Pt₄-O₂)

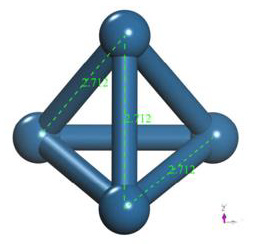
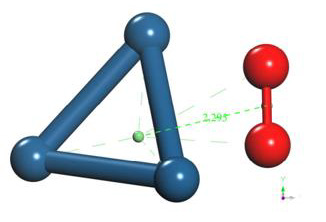
The output of the geometry optimization of platinum cluster (Pt₄), which has a Pt-Pt bond distance of 2.712Å in the simulation as shown in Figure 16, agrees with the experimental value of 2.68Å [13].

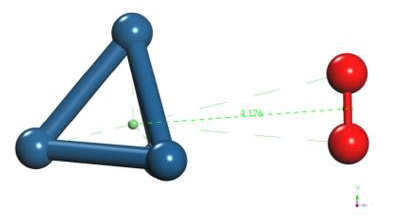
The geometry optimization calculation of the platinum cluster is accomplished with the oxygen molecule. A the input, the platinum cluster is placed at a distance of 4.176Å from the oxygen molecule to carry out the optimization (Figure 17).

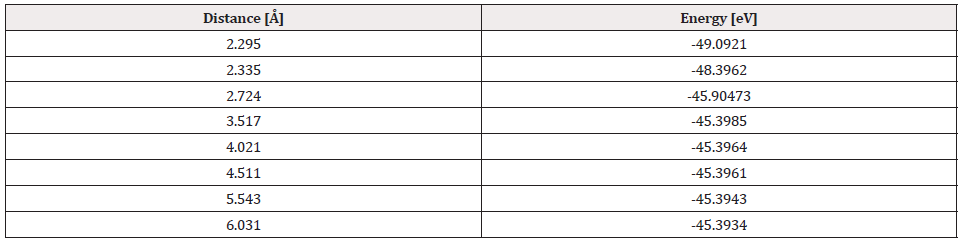
The geometry optimization gives an equilibrium distance of 2.295Å and an energy of -49.092 eV. The connectivity calculation is applied as shown in Figure 18.

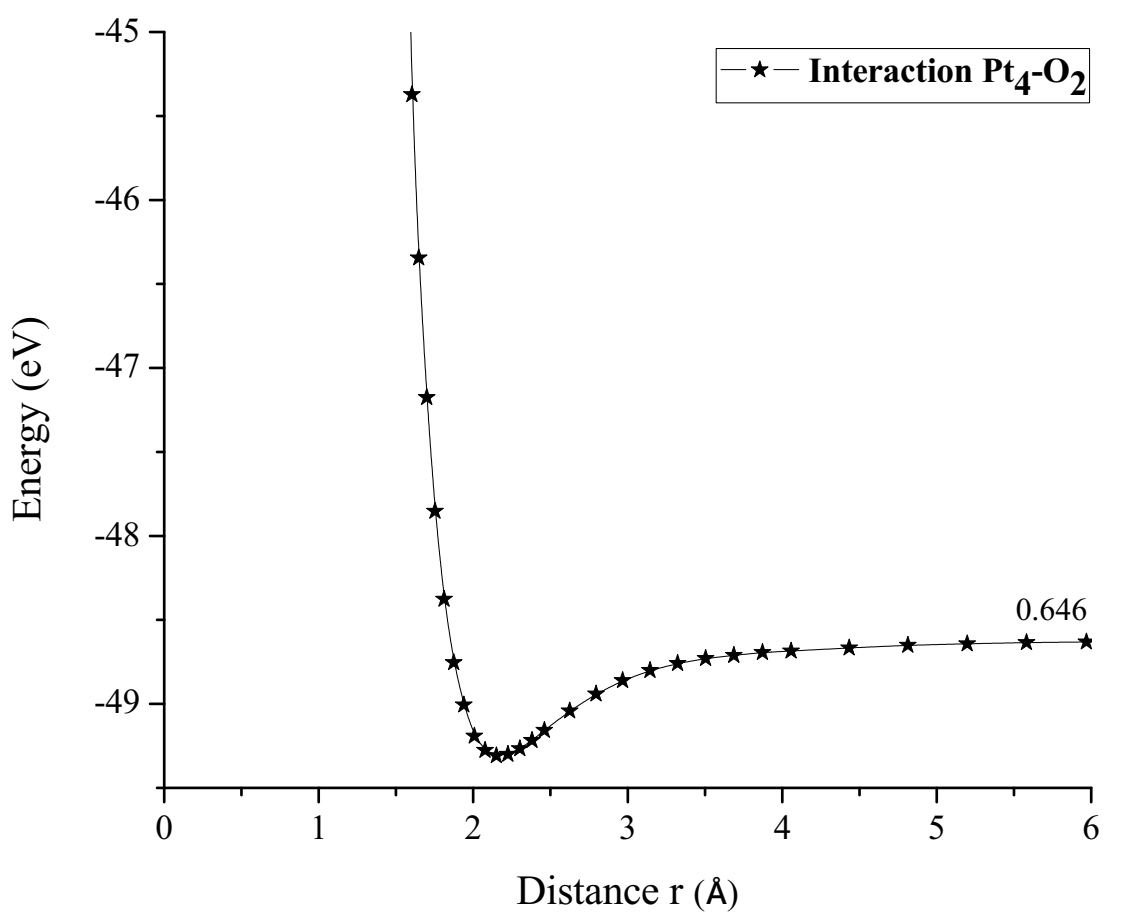
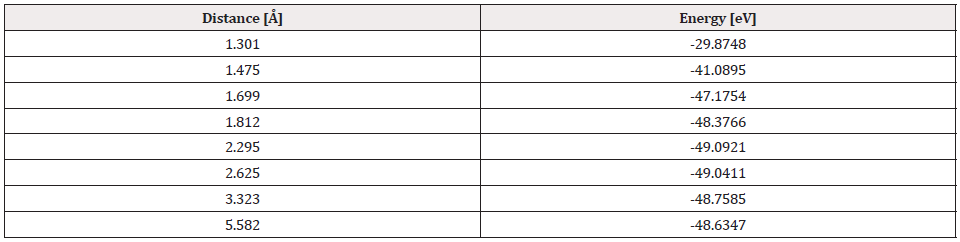
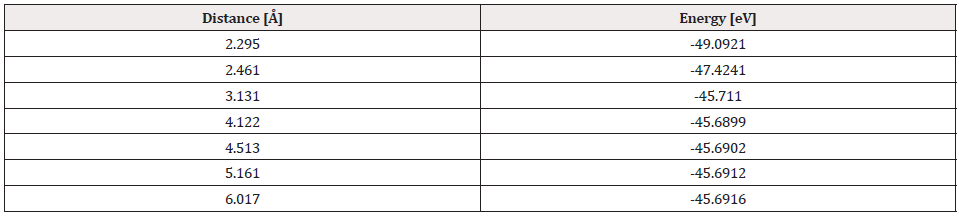
The potential energy well of the Pt₄-O₂ interaction is calculated as shown in Figure 19, considering fixed the platinum cluster, and the oxygen molecule is moved away and closer from 0.1Å to 0.1Å. At each distance, an energy value is obtained as shown in Table 6, for which a potential well size of 0.646eV is obtained. The experimental value of the interaction is equivalent to 0.669eV [19], and there is an error of 3.5%.

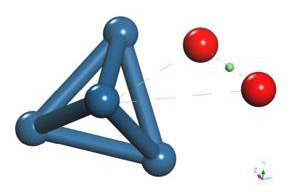
The Pt₄O₂ complex formed at the minimum of the potential energy curve is broken by taking out one oxygen atom to free it, to obtain Pt₄O + O as products. The Pt₄O₂ complex molecule has an equilibrium distance of 2.295Å between Pt₄ and O₂, and an equilibrium energy of -49.092eV with an energy well depth 0.646eV potential as shown in Figure 19. The output after geometry optimization gives 1.3Å for O-O bond length,

From the already optimized system we fixed the platinum cluster and one oxygen atom, later the oxygen atom not fixed is moved away horizontally until the energy is constant (Figure 20).

Figure 16: Optimized Platinum Pt4 Cluster.

Figure 17: Molecular arrangement of the platinum cluster with the oxygen molecule (input)

Figure 18: Geometry optimization of the Pt₄-O₂ molecular arrangement (output)

Figure 19: Potential energy curve of the Pt₄-O₂ interaction.

Figure 20: Moving the oxygen atom away horizontally and breaking the O₂ molecule.

Table 6: Distances and Energies of the Pt₄-O₂ Interaction.

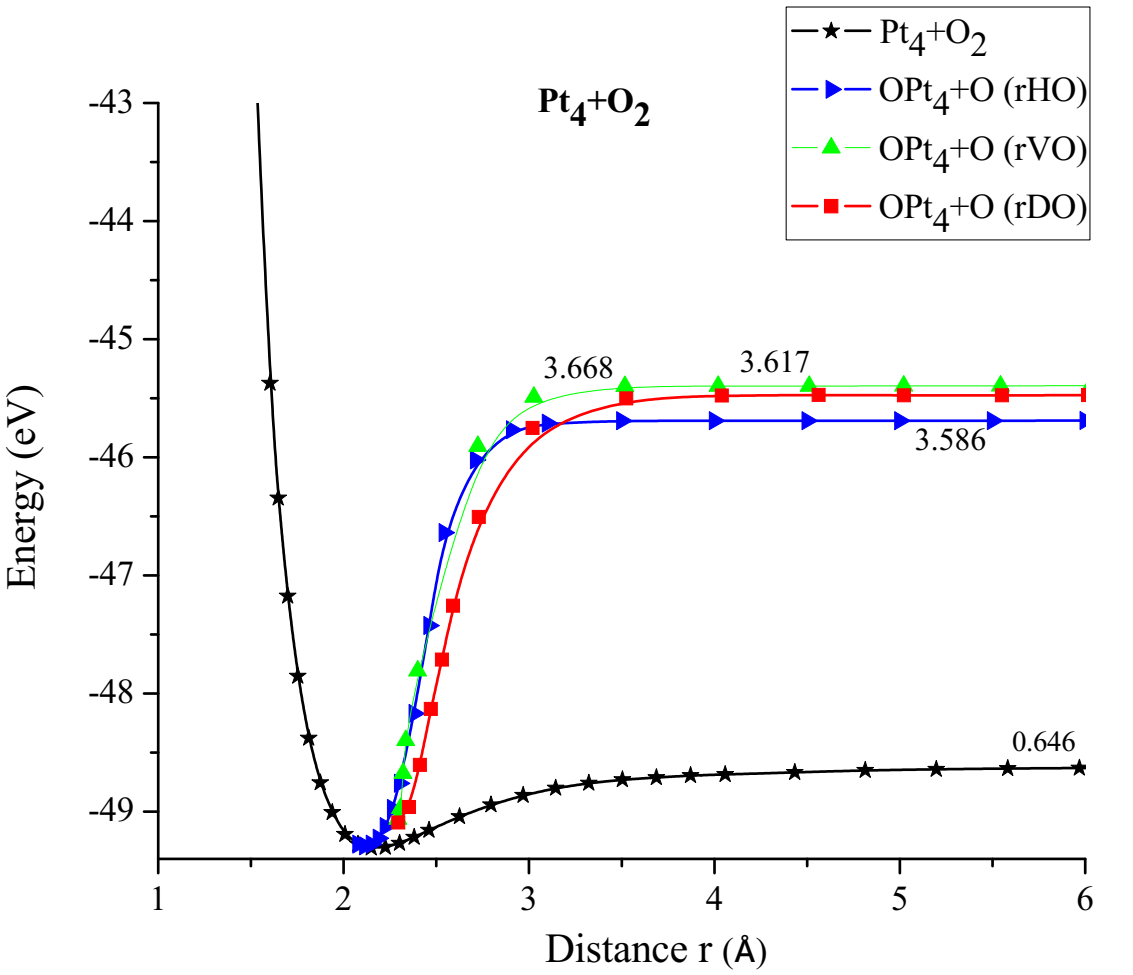
As shown in Figure 20, the platinum cluster breaks the O₂ molecule as it moves horizontally towards and away an oxygen atom. The energy curve was constructed, in each distance an energy value was obtained as shown in Table 7, it was found that the well size is 3.586eV (Figure 21).

The already optimized Pt₄ + O₂ system is taken again, fixing the platinum cluster and an oxygen atom, later an oxygen atom not fixed is vertically moved away until the energy is constant (Figure 22).

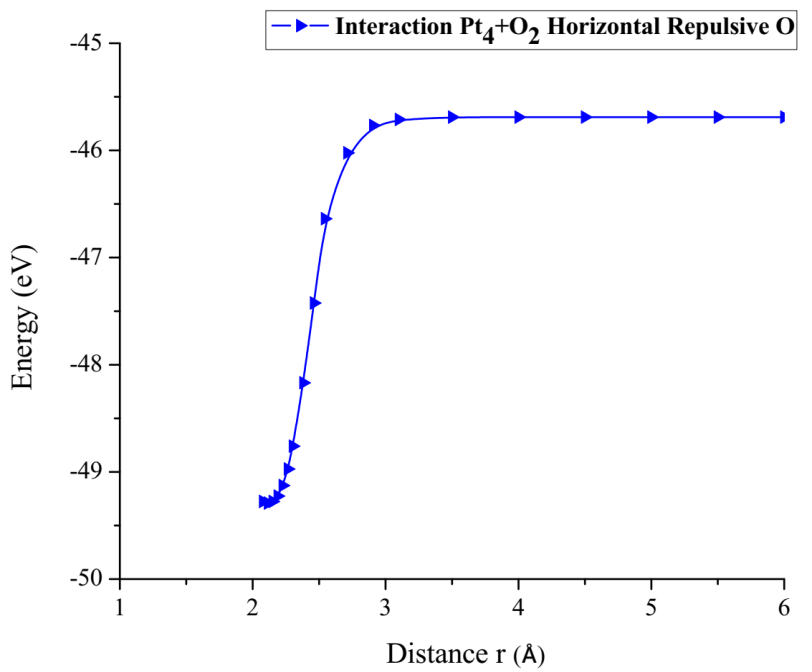
Figure 21: Potential energy curve of the breakdown of the O₂ molecule, moving the oxygen atom away horizontally.

Figure 22: Moving the oxygen atom away vertically and breaking the O₂ molecule.

Table 7: Distances and Energies of the Pt₄-O₂ Interaction (Horizontal).

The energy curve for breaking the O₂ molecule was constructed vertically, at each distance an energy value is obtained as shown in Table 8, it was found that the well size is 3.668eV (Figure 23).

Finally, the optimized Pt₄ + O₂ system was taken up again, we fixed the platinum cluster and an oxygen atom, later the oxygen atom began to move away, which was not fixed diagonally until the energy was constant (Figure 24). At each distance, an energy value was obtained as shown in Table 9.

The energy curve for breaking the O₂ molecule was constructed diagonally, and the well size was found to be 3.617eV (Figure 25).

In Figure 26 it is found that the inflection points, vertical repulsive oxygen (vrH) = 3.668Å, diagonal repulsive oxygen (drH) = 3.617Å, horizontal repulsive oxygen (hrH) = 3.586Å, consequently it is found that hrH breaks before drH and this before vrH, and with the energies vrH = 3.668eV, drH = 3.617eV, hrH = 3.586eV. These correspond to what it takes on average almost the same amount of energy to break the oxygen molecule O₂.

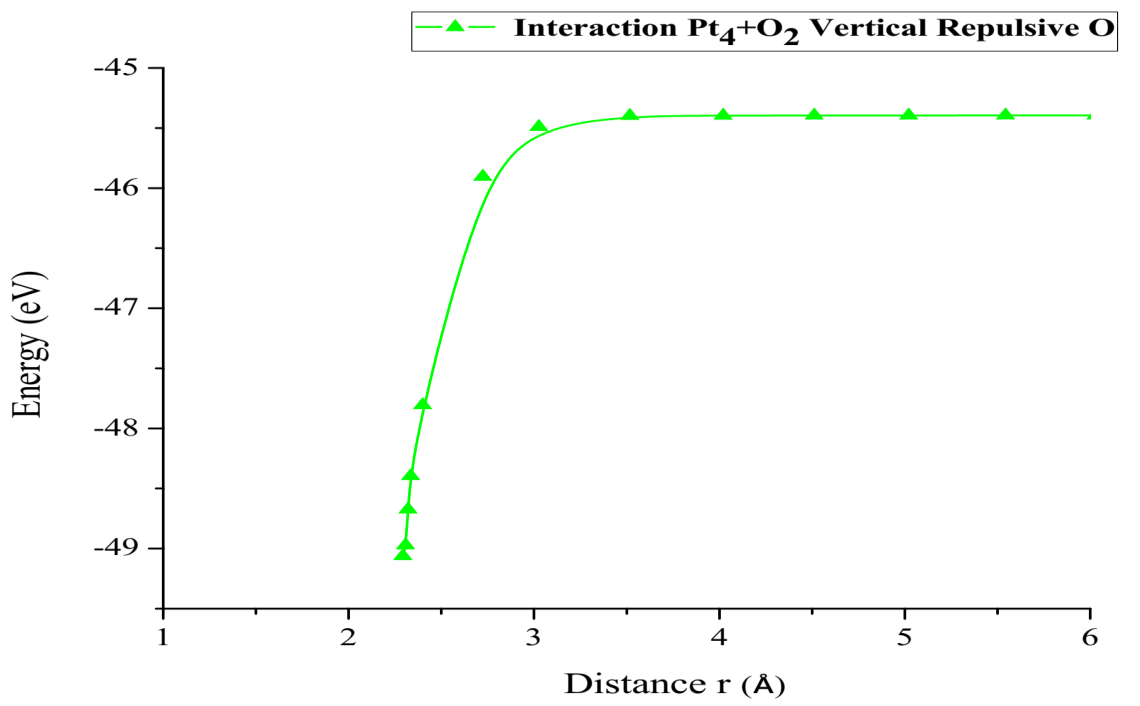
Figure 23: Potential energy curve of the breakdown of the O₂ molecule, moving the oxygen atom away vertically

Figure 24: Moving the oxygen atom away diagonally and breaking the O₂ molecule.

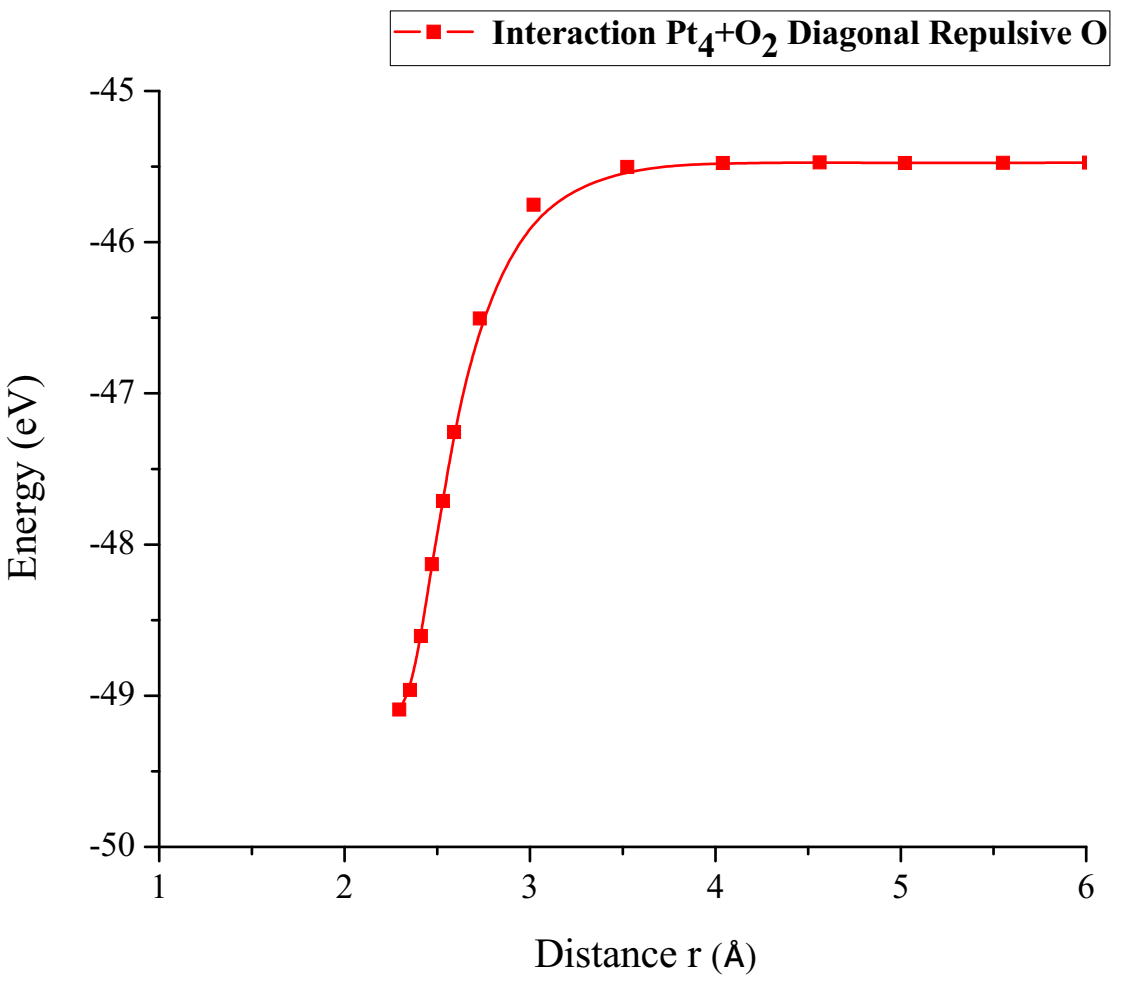
Figure 25: Potential energy curve of the breakdown of the O₂ molecule, moving the oxygen atom away diagonally.

Figure 26: Comparison of Interactions.

Table 8: Distances and Energies of the Pt₄-O₂ Interaction (Vertical).

Table 9: Distances and Energies of the Pt₄-O₂ Interaction (Diagonal).

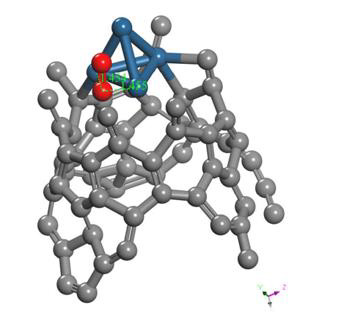
Interaction of the C₆₀Pt₄ System with an Oxygen molecule (C₆₀Pt₄-O₂)

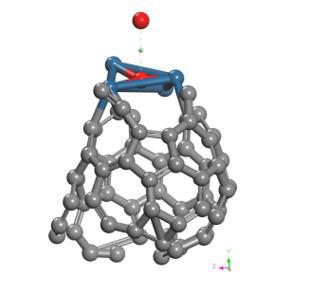
The C₆₀Pt₄ system was placed at 1.45 Å from the O₂ molecule as shown in Figure 27.

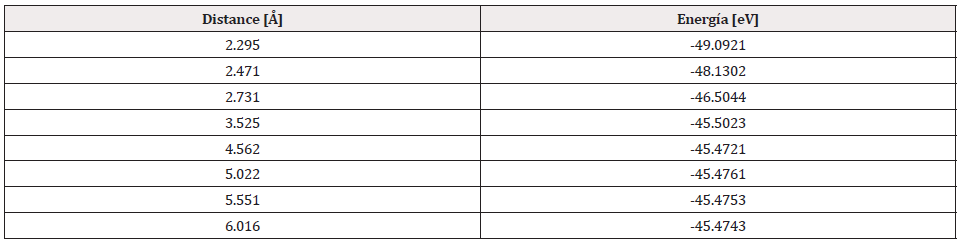
The geometry optimization calculation of the C₆₀Pt₄ system is accomplished with the oxygen molecule. The geometry optimization gives an equilibrium distance of 2.048Å and an energy of -451.2475 eV, and the connectivity calculation is applied (Figure 28).

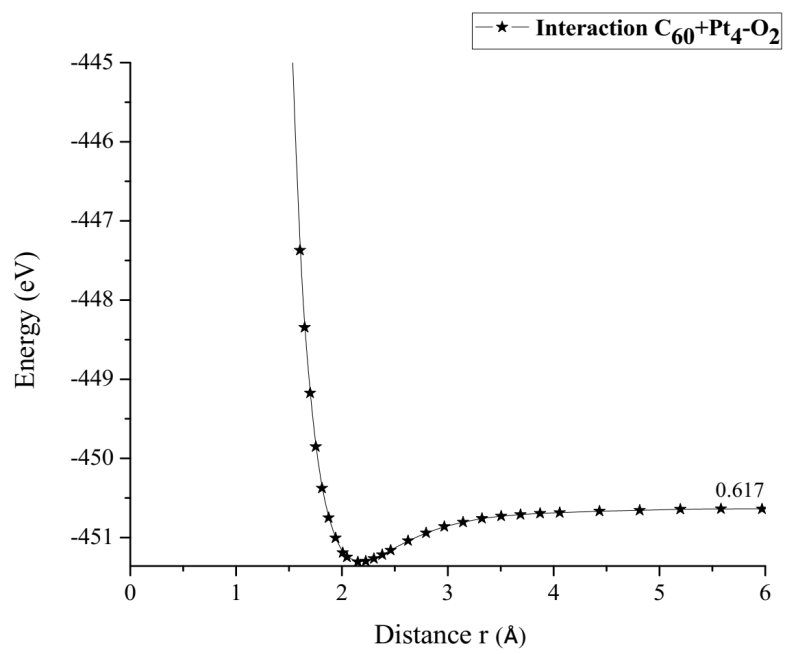
The potential energy well of the C₆₀Pt₄-O₂ interaction is calculated as shown in Figure 29, and for this the C₆₀Pt₄ system is set fixed, and the oxygen molecule is moved away and closer from 0.1Å to 0.1Å. At each distance, the corresponding energy value is obtained as shown in Table 10, for which a potential well size of 0.617eV is obtained, the experimental value of the interaction is equivalent to 0.619eV [19] there is an error of 0.3%, then the agreement is very good.

Figure 27: Molecular arrangement of the C₆₀Pt₄ system with the oxygen molecule (input).

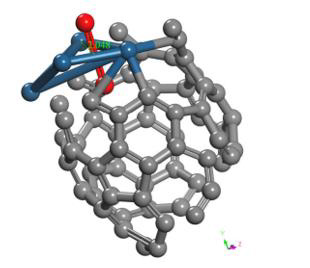
Figure 28: Geometry optimization of the molecular arrangement C₆₀Pt₄-O₂ (output) of an intermediate complex.

Figure 29: Potential energy curve of the C₆₀Pt₄-O₂ interaction.

Table 10: Distances and Energies of the C₆₀Pt₄-O₂ Interaction.

The C₆₀Pt₄-O₂ system is carried out to break the oxygen molecule, for obtaining C₆₀Pt₄O + O products. Having Started with C₆₀Pt₄-O₂ system already geometrically optimized (Figure 28), which has an equilibrium distance of 2.048Å between C₆₀Pt₄-O₂ and an equilibrium energy -451.2475eV with a potential energy well depth of 0.617eV.

From the already optimized system we fixed the C₆₀Pt₄ system and an oxygen atom, later the non-fixed oxygen atom is moved away horizontally until the energy is constant. At each distance, the corresponding energy value is obtained, as shown in Table 11 (Figure 30).

As shown in Figure 30, the C₆₀Pt₄ system breaks the oxygen molecule (O₂) when step by step one oxygen atom is horizontally moved away and closer. The energy curve is constructed and the potential well size is found to be 2.766 eV (Figure 31) (Table 11).

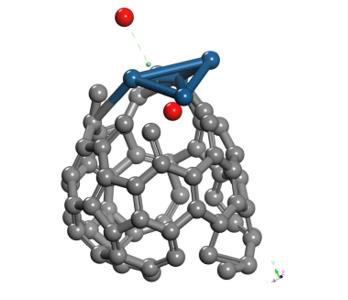
The already optimized C₆₀Pt₄-O₂ system is taken up again, fixing the C₆₀Pt₄ system and an oxygen atom, later an oxygen atom that was not fixed vertically began to move away until the energy was constant (Figure 32).

At each distance, an energy value is obtained as shown in Table 12, which is used to vertically build the energy curve for breaking the O₂ molecule. It was found that the well size is 2.798eV (Figure 33).

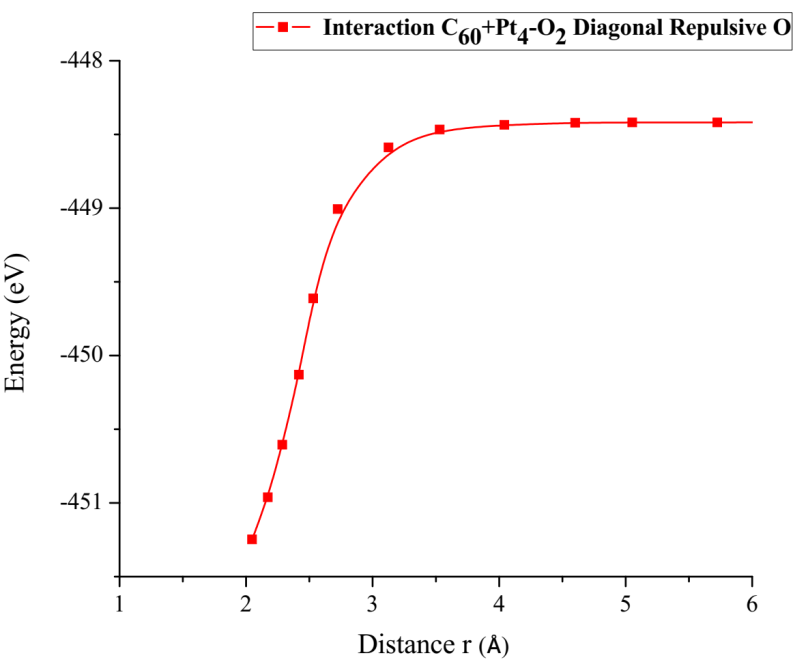
Finally, the optimized C₆₀Pt₄-O₂ system was taken again, we fixed the C₆₀Pt₄ system and an oxygen atom, later the other oxygen atom is diagonally moved away, until the energy is constant (Figure 34).

At each distance, an energy value was obtained as shown in Table 13, the energy curve for breaking the O₂ molecule is diagonally constructed, and the well size is found to be 2.829eV (Figure 35).

In Figure 36, for the inflection points, vertical repulsive oxygen (vrH) = 2.798Å, diagonal repulsive oxygen (drH) = 2.829Å, horizontal repulsive oxygen (hrH) = 2.766Å, it is found that hrH breaks before vrH and this before drH, with energies vrH = 2.798eV, drH = 2.829eV, hrH = 2.766eV, respectively. These values agree with the same amount of energy to dissociate the oxygen molecule O₂.

Table 11: Distances and Energies of the C₆₀Pt₄-O₂ Interaction.

Table 12: Distances and Energies of the C₆₀Pt₄-O₂ Interaction (Vertical).

Table 13: Distances and Energies of the C₆₀Pt₄-O₂ Interaction (Diagonal).

Figure 30: Moving the oxygen atom away horizontally for breaking the O₂ molecule.

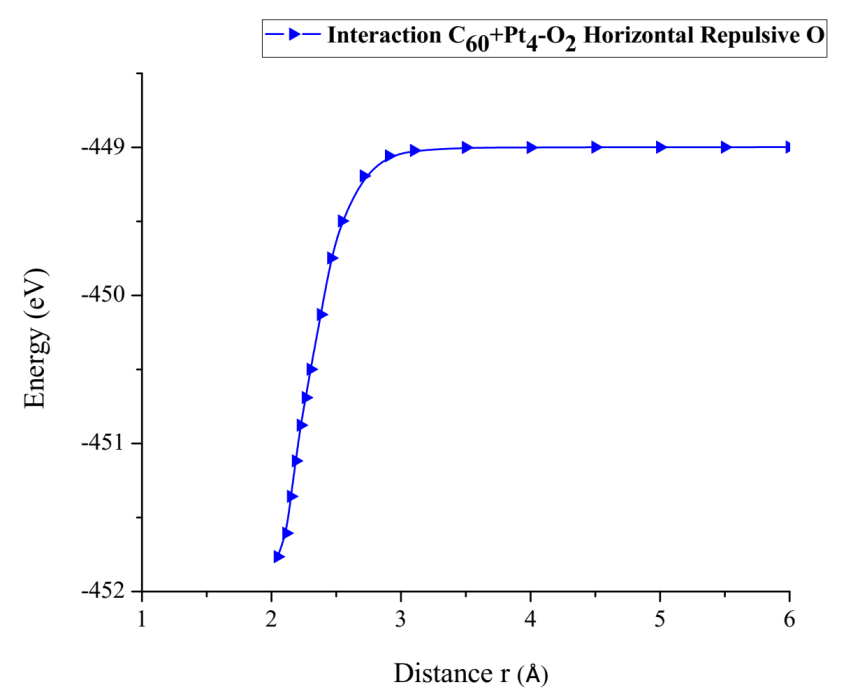
Figure 31: Potential energy curve of the breakdown of the O₂ molecule, moving the oxygen atom away horizontally.

Figure 32: Moving one oxygen atom away vertically for breaking the O₂ molecule.

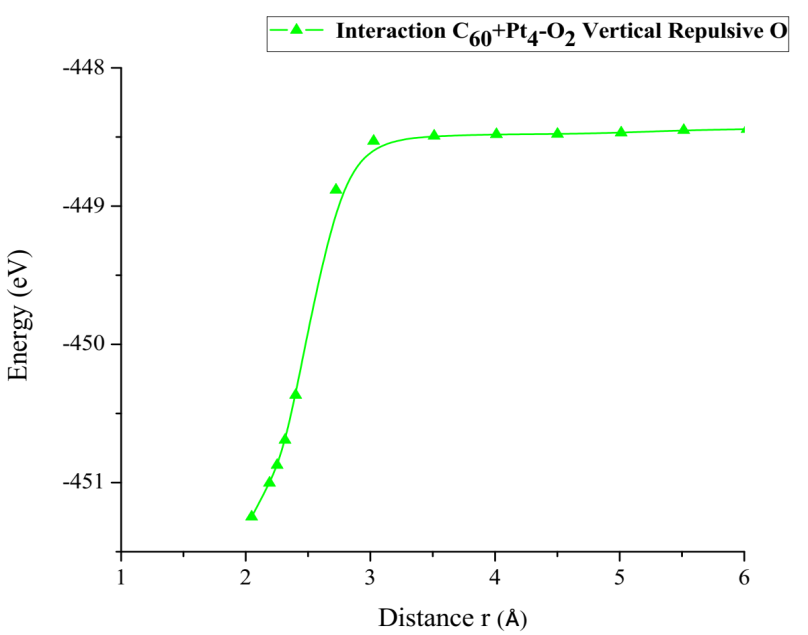
Figure 33: Potential energy curve of the breakdown of the O₂ molecule, moving the oxygen atom away vertically.

Figure 34: Moving diagonally the oxygen atom away and breaking the O₂ molecule.

Figure 35: Potential energy curve of the breakdown of the O₂ molecule, moving diagonally the oxygen atom away.

Figure 36: Comparison of interactions for breaking an oxygen atom in several configurations.

Conclusions

Our results match with DFT calculations supported on experimental data. The interaction among oxygen molecules in different configurations and different forms of platinum has application in this case on hypoxia which is a blood cancer and on electrodes of fuel cells through calculated energies. DFT calculations might help in designing intermediate molecule complexes for treatment of this kind of hypoxia cancer. In addition, the catalytic support C₆₀Pt₄ breaks the oxygen molecule O₂, and it is found that hrH breaks before vrH and this before drH. With energies hrH = 2.766eV, vrH = 2.798eV, drH = 2.829eV, these correspond to what it takes on average almost the same amount of energy to dissociate the oxygen molecule O₂.

References

• Galsky MD, Camacho LH, Chiorean EG, Mulkerin D, Hong DS, et al. (2012) Phase I study of the effects of renal impairment on the pharmacokinetics and safety of satraplatin in patients with refractory solid tumors. Ann Oncol 23(4): 1037-1044.
• Doshi G, Sonpavde G and Sternberg CN (2012) Clinical and pharmacokinetic evaluation of satraplatin. Expert Opin Drug Metab Toxicol 8(1): 103-111.
• Galsky MD, Seng S, Camacho LH, Chiorean EG, Mulkerin D, et al. (2011) Retrospective analysis of satraplatin in patients with metastatic urothelial cancer refractory to standard platinum-based chemotherapy. Clin Genitourin Cancer 9(1): 27-30.
• Wexselblatt E, Gibson D, Inorg J (2012) What do we know about the reduction of Pt(IV) pro-drugs?. J Inorg Biochem 117: 220-229.
• Ming M, Ma ZL, Xu YT, Sun FY, Cui XH, et al. (2017) Carboplatin-based Nanomedicine to Enhance the Anticancer Effect in SK-NEP-1 WilmsꞌTumor Cells. Iran J Pharm Res 16(4): 1305-1311.
• Katsounaros I, Cherevko S, Zeradjanin AR, Mayrhofer KJJ (2014) Oxygen electrochemistry as a cornerstone for sustainable energy conversió Angew Chemie Int Ed 53(1): 102-121.
• Xiao F, Xu GL, Sun CJ, Hwang I, Xu M, et al. (2020) Nano Energy 77: 105192.
• Cherevko S, Kulyk N and Mayrhofer KJJ (2016) Nano Energy 29: 275-298.
• Zeng Z and Greeley J (2016) Nano Energy 29: 369-377.
• Du L, Shao Y, Sun J, Yin G, Liu J, et al. (2016) Nano Energy 29: 314-322.
• De La Mora K, Pacheco Sánchez JH (2020) Am J Biomed Sci & Res 6(6): 488-489.
• Mayrhofer KJJ, Ashton SJ, Meier JC, Wiberg GKH, Hanzlik M et al. (2008) Non-destructive transmission electron microscopy study of catalyst degradation under electrochemical treatment. J Power Sources 185(2): 734-739.
• Qi Q, Liu H, Feng W, Tian H, Xu H el al. (2015) Comput Mater Sci 96: 268-276.
• Maynard AT, Huang M, Rice WG and Covell DG (2002) Reactivity of the HIV-1 nucleocapsid protein p7 zinc finger domains from the perspective of density-functional theory. Proc Natl Acad Sci 95(20): 11578-11583.
• Wang X, Li X, Liao S and Li B (2018) Comput Mater Sci 149: 107-114.
• Cristian AEM, Guerra J, Lopez JM, Figueredo SF, Muñoz AE (2015) Quim Nova 1-6.
• Estrada E, Phys J (2002) Chem A
• Huber KP and Herzberg G (1984) Molecular Spectra and Molecular Structure. Dover Pub 3: 1385.
• Dean JA (1999) Lange's Handbook of Chemistry 15th edition, Section 4. Y. Luo, Properties of atoms, radicals, and bonds, McGraw-Hill.
• Valenzuela Hermocillo EA, Pacheco Sánchez JH, Rivas Castro SF (2019) Revista de Energía Química y Física 6(19): 31-38.
• Pacheco JH, Zaragoza IP, García LA, Bravo A, Castillo S, et al (2006) Rev Mex Fís 52(2): 172-177.
• Pacheco JH, Bravo A, Novaro O (2006) Rev Mex Fís 52(5): 394-397.