Significance of MD Simulation in Pharmaceutical Sciences: A Review

Introduction

Computational Chemistry

The two most familiar branches of science are experiment and theory. In theory, claims have been made that might be falsifiable or predictions that can either be true or false on the basis of models represented while the experiments testify these predictions by accepting or rejecting true or false theories. Now the third pillar, which is currently emerging rapidly in academic research, is simulation. As we know, theories basically are conceptual ideas or equation and usually these equations are quite complexed and sometimes they are too complicated to solve with unobvious conclusions so instead of going towards expensive time consuming experimental methods, these theories can be assist by performing simulations, so basically computational chemistry [1-3] is the use of simulation in context of chemical systems or models. By using computational methods we simulate these complexed equations of theories and also sometime the experimental results generate some complex data that can be simulated into simplified conclusions by interpreting the experimental data. Sometimes there are different parameters in these equations of theories and by using experimental methods different values set for these parameters for simulation while giving solutions for these equations [4].

Molecular Mechanics and Force Fields

Molecular mechanics can be defined as group of models which implement empirical, algebraic, atomistic energy function for any molecular system. Here the empirical and algebraic energy function represents the experimental data, formulas, and equations and the atomistic energy function describe the level of details at individual atomic level for chemical system and biological molecules [5].

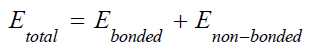
Here the total energy of the system consists of two components i.e. bonded energy and non-bonded energy [6].

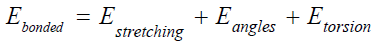
Bonded energy included stretching energy between atoms, angle energy and torsion.

While non-bonded energy consists of electrostatic energy and Van der Waal energy [7,8].

Force Field

The reliance of energy of a molecular system on the coordinates of its atoms or particles is mathematically expressed as force field [9]. Force fields are basically the expression of parameterized empirical energy, involved in the interactions at atomic level of chemical systems containing large number of molecules or biomolecular systems [10,11]. In these systems evaluation of energy with high level calculations are very difficult, so instead of solving Schrodinger’s equation [12] by complex quantum mechanics (QM) calculations, molecular mechanic (MM) methods using force fields are appropriate. Force field can be implemented on either large systems of macromolecules like protein receptors [13,14], lipid bilayers [15,16] and nucleic acid [17,18] or smaller molecular system having interaction between few molecules or interaction of molecules with the solvents [19,20]. Depending upon the nature of molecular system force field can be varied. For larger molecular systems we have number of force fields such as AMBER [21], CHARMM [22,23] and GROMOS [24] and for smaller molecular system we have universal force field (UFF) [25], MMFF94 or MFF94x [26]. In any force field the potential energy between the particles is described in functional form and this potential energy functional form consist of two forms bonding potential [27] and non-bonding potential [28].

MMFF94 Force Field: Merck molecular force field (MMFF) was first developed by Merck research laboratories using computational data for its parameterization. The commencing published version of MMFF is MMFF94 [26]. In computational chemistry MMFF94 force field implemented or parameterized in MD simulation studies of gas phase small organic molecules [29]. It is applied in simulating the thermodynamic properties, structure, conformation and interactions of smaller molecules with limited number of atoms [30,31]. In some studies it has been reported that the analysis of proteins in organic solvents by parameterization of MMFF94 force field showed weak non-bonded interactions as compare to other force fields like AMBER or OPLS-AA [32]. Most widely MMFF94 force field is implemented in molecular modelling, i.e the computational method of characterizing, visualization and analysis of the structure [33] of pharmaceutical drugs [34] or other pharmacologically active compounds [35] or metal complexes [36].

OPLS Force Field: Optimized potentials for liquid simulations (OPLS) first developed by Prof William L. Jorgensen [41] is similar to AMBER force field and implanted in characterizing simulation studies of biomolecules [42] and optimized for liquid-state and gas phased parameters [43]. Depending upon the nature and type of atoms or molecules there are different set of parameters like OPLSUA (united atom) [44] and OPLS-AA (all atoms) [45].

CHARMM Force Field: Chemistry at Harvard macro molecular mechanics (CHARMM) is basically a set of different force fields that are developed by group of scientists working with Martin Karplus at Harvard [22]. It is implemented for all types of atoms and parameterized for simulation of proteins [46], lipids [47], RNA, DNA [23] and other biomolecules but not favorable for smaller organic molecules. It is reported that CHARMM is compatible diversified force field having potential energy functions for bond angle, torsion, dihedrals, out of plane motions and non-bonded electrostatic and Van der Waal interactions for different molecular systems [48].

Quantum Mechanics

In this section a brief introduction of quantum mechanics is discussed including theoretical background and different approaches of quantum mechanics and how it is differentiated from the classical mechanics.

Erwin Schrodinger in 1926 [49], expressed mathematical equation known as Schrodinger’s equation of wave function ᴪ or time dependent Schrodinger’s equation (TDSE) which described any system with respect to time.

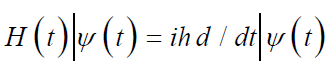
This equation gives the idea about the wave nature of electrons, and it replaces the classical mechanics Newton’s equation F= ma which applies to Newtonian systems while the Schrodinger’s equation applies to quantum systems and describes the system three-dimensional wave function [50]. Another simplified form of Schrodinger’s equation is time independent Schrodinger’s equation (TISE) or eigenvalue equation.

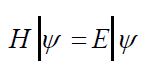
In this linear partial differential equation ‘E’ is a constant represents energy level of system or in algebraic term it is the eigenvalue of corresponding Hamiltonian and ‘H’ is the Hamiltonian operator, define as a set of mathematical operators explaining all the interactions dictating the state of system which can be interpreted as the total energy of particle [50]. Total energy is associated with kinetic energy T and potential energy V.

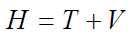
Both the kinetic energy T and potential energy V further mathematically expressed as;

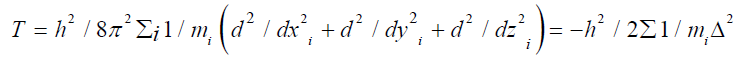
Here, in the system of electrons and neutrons ‘m’ represents the mass of ith particle and ‘h’ is Planck’s constant.

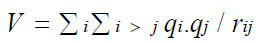
Here the potential energy is the columbic interaction of particles within the single atom, without considering the external field.

Interpretations and Approximations of Schrodinger’s Equation: Schrodinger expressed this mathematical equation of wave function for hydrogen atom and this equation is applicable on single electron system like hydrogen but in terms of molecular level or different chemical systems it is too complicated to analyze the wave function by the derivatization of Schrodinger’s equation. To overcome this complication, different scientist proposed different approximations and interpretations in the Schrodinger’s equation and simplify the methods for quantum mechanics simulation of different chemical systems [51]. Some of these approximations include Born-Oppenheimer approximation [52], which neglects the electron- neutron attractive potential energy term and only consider the neutron-neutron repulsive potential energy term as a constant in a given molecular system. The Hatree-Fock method is another approach to solve the Schrodinger’s equation [53] and calculate the energy of molecular system considering spin orbital of electron as wave function. Many other methods and different approaches have been introduced by different scientists to give the solution of Schrodinger’s equation for different molecular systems at different levels. Some of these methods include multideterminant methods [54], pair methods, semi empirical methods, density function theory [55] etc.

Molecular Dynamics Simulation

Techniques of Simulation: The fundamental purpose for simulation is to analyze the molecular system with respect to the structure and interaction of concerned molecules. There is a wide range of simulation techniques but the two basic techniques include molecular dynamics (MD) and Monte Carlo (MC) simulation and all other techniques are hybrids of these two.

Molecular Dynamics: Molecular dynamics is simulation technique that interprets classical Newton’s equation of motion to analyze the trajectories, movements and interactions in a given molecular system modelled at atomic level [3,56-58]. These atoms and molecules are allowed to simulate for a fixed period of run time and their potential energies and forces within the molecules analyzed by interpretations of molecular mechanics force field. Molecular dynamics simulation gradually analyzes the solution of equation of motion and for any molecular system it can be written as;

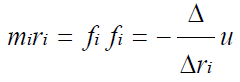
By solving equation of motion we can calculate the forces f acting on each atom of molecular system and acceleration experienced by these atoms and these forces are derived from the potential energy U (r^N) of these atoms represented as set of 3N coordinates.

MD Integration Algorithms: In any molecular system of MD simulation, the potential energy is the function of atomic position considering all three coordinates (3N). The Newton’s equation of motion cannot be solved analytically because of complexed potential energy function. In order to get the numerical solution of this equation, different algorithms have been proposed by integrating the equation of motion. Depending upon the nature of molecular system, the appropriate algorithm was chosen for MD simulation [59]. These algorithms consider appropriate for the simulation on the basis of its computational efficiency, the duration of run time it can provide for simulation and its ability to conserve energy and momentum of molecular system. Every integration algorithm suggests the position, velocities and acceleration can be derived from Taylor’s series [60] expansion:

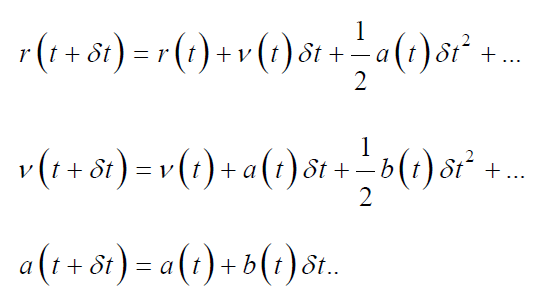
In these mathematical expressions ‘v’ represents velocity, ‘r’ is position and ‘a’ is acceleration.

Verlet’s Algorithm: Verlet’s algorithm is derived as;

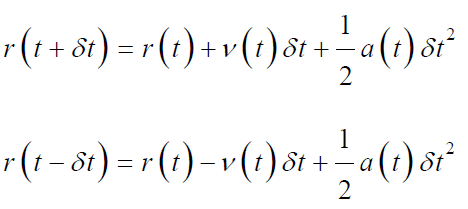
By the combination of above two equations we obtained;

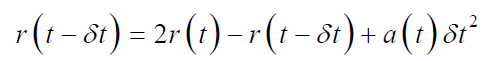
In this algorithm, the position and acceleration at time ‘t’ is used to estimate the new positions at time (t+δt), without any use of explicit velocities. Verlet’s algorithm is beneficial in straight forward molecular systems with adequate need of energy. But the precision of this algorithm is not highly accurate [61,62].

The Leap-frog Algorithm:

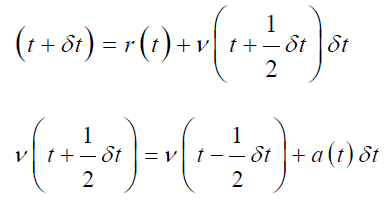
in leap-frog algorithm both velocities and position can be estimated by leaping over each other, first the velocity ‘v’ is calculated at time (t+1/2 δt) then by using this velocity, position ‘r’ can be estimated at time (t+δt) [63]. This is the benefit of this algorithm that velocities can be estimated explicitly for any particle or atom in the MD simulation but the drawback is that the velocity and position cannot be calculated explicitly [64]. Further, the velocity at any time ‘t’ can be evaluated by this mathematical expression;

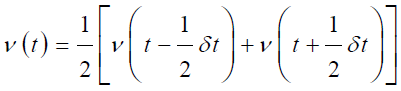
Beeman’s Algorithm: This algorithm is derived from Verlet’s algorithm;

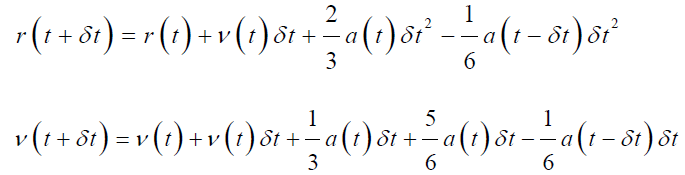
Beeman’s algorithm evaluated the velocity of particles more precisely by providing more accurate expression and conserve the energy as well. The only drawback for this algorithm is the computational cost for complex calculations [65].

Ensembles in MD Simulation: To perform MD simulation for different molecular systems we have different ensembles that represent different microscopic states for identical macroscopic or thermodynamic systems [66]. Ensembles of different characteristics are discussed here.

Micro-canonical Ensemble (NVE): NVE represents an isolated system having specified number of molecules N, stable volume V and fixed energy E of the system. Here the trajectories represent the exchange of potential energy and kinetic energy keeping the total energy constant. As the system in NVE ensemble is isolated, the temperature of the system is subjected to vary during the simulation and the system can be referred as adiabatic system with no exchange of heat so in NVE macromolecular systems of proteins, the temperature usually raised during simulation of exothermic conformation variations or interactions within the molecular system [67,68].

Canonical Ensemble (NVT): NVT is a set of molecular system which characterized the thermodynamic properties with constant no of atoms N, fixed volume V and fixed temperature T as well. Here an external heat reservoir is used to control the temperature of molecular system. There are set of different algorithms that are used to control the temperature of NVT ensemble system [68]. One of the commonly used algorithms is Berendsen algorithm [69], in this algorithm the temperature is controlled by scaling the velocity of each particle by a factor λ at every point where the exchange of heat energy is done by heat reservoir. Mathematically the factor λ is expressed as;

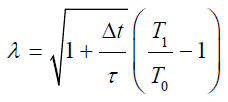
in this equation τ is the relaxation time, t is integration time step and T1 and T0 represents the target temperature and self-point temperature respectively. This algorithm is highly efficient incontrolling temperature of heat reservoir. There is also an alternative algorithm that used the coefficient fraction, which influence the forces acting on all particles, to control the temperature of heat reservoir. This algorithm is known as Nose- Hoover chain algorithm [70].

Isobaric-isothermal Ensemble (NPT): NPT ensemble characterized by constant number of atoms N, constant pressure P and constant temperature T. In this ensemble to control the pressure of the molecular system, a barostat is also needed in addition to the thermostat. NPT ensemble systems are usually significant in simulation of systems containing biological membranes [68,71].

Grand canonical ensemble (μVT): μVT ensemble characterized the thermodynamics of molecular system by considering constant chemical potential μ, constant volume V and constant temperature T [68].

Literature Review of MD Simulation of Pharmaceutical Products

Characterization of Metallic Drug Nanoparticles by MD Simulation

Theoretical approach of MD simulation, in companionship with experimental methods, is significant in the characterization of metallic nanoparticles at atomic level [72]. The potential of silver nanoparticles in the field of medical sciences is known for centuries, MD simulation is one of the advanced cost-effective techniques for researchers to characterize important features of silver nanoparticles. On March, 2020, Sohraby performed MD simulation of silver nanoparticles in order to theoretically estimate the potential of rosemary active compounds in coating of nanoparticles and analyze the dynamic behavior of these compounds with silver nanoparticles [73]. In 2018 and 2019, M.M. Blazhynska and his associates study the polarization effects of different force fields in MD simulation of silver nanoparticles and determine the morphological stability of different shapes of silver nanoparticle by analyzing the effect of temperature and binding energy by MD simulation [74,75]. In another study, complete melting, sintering and surface pre-melting point of silver nanoparticles was analyzed by MD simulation [76,77]. L Chen in 2017 perform the MD simulation of silver nanoparticles to characterized the physicochemical properties, stability of lattice structure and surface energy of NP [78]. In the research work of Paul Martin, he studied the nanotoxicology by the MD simulation of silver nanoparticles and analyzed that the reactivity of nanoparticles can be influence by the structure and size variations and by controlling the size, toxicity profile of nanoparticles can be managed [79].

Characterization of Antiviral Drugs by MD Simulation

In 2013, the antiviral resistance mutation was studied in HBeAg positive patients, administering the entecavir therapy. Molecular docking and MD simulation was performed on 3D model of HBV polymerase to analyze the antiviral resistant mutations [80]. In 2015, Dante Morgnanesi presented his work to explain the importance of computational chemistry and molecular dynamics simulation in the discovery of hepatitis B antiviral drugs. This study was focused on three computational techniques including homology modeling to analyze the structure and conformation of protein HBV polymerase, molecular docking to understand the antagonizing mechanisms of hepatitis B antiviral drugs and molecular dynamics simulation to study the molecular motions and stability profile of antiviral drugs [81]. Another computational study was done for the design and pharmacological analysis of antihepatitis B drugs, by molecular docking and molecular dynamics simulation. 500 picoseconds simulation at constant pressure was run to get the relative stability of antiviral drugs [82]. In 2014, insilico computational techniques were studied for the identification of novel HBV target NTCP, sodium taurocholate co‐transporting polypeptide. Molecular modelling and screening characterization of antiviral drugs was done by molecular dynamics simulation and experimental validation and proposed a significant target for anti HBV drugs [83].

Conclusion

In modern research, simulation is the bridge between the theoretical and experimental science. This technique made it possible to visualize and characterize the individual matter, its internal or free energies and its motion as a function of time. Now molecular dynamics simulation techniques has become a crucial tool in analysis, modelling and characterization of basic physical, structural and functional properties of biological molecules specially proteins, amino-acids or enzymes. This study elaborates the significance of molecular dynamics simulation in analysis of antiviral drugs, metallic nanoparticles and other pharmaceutical products and it helps to understand the nature of these drugs at the atomic level and this analysis could be used to establish a better pharmacokinetic and stability profile and to get the enhanced and safer drug delivery to its target site.

References

• Greiner W (2001) Quantum mechanics: an introduction. Springer Science & Business Media.
• Jensen F (2016) Introduction to computational chemistry. John wiley & sons.
• Cramer C J (2004) Essentials of computational chemistry: theories and models. John Wiley & Sons.
• Allen M P (2004) Introduction to molecular dynamics simulation. Computational soft matter: from synthetic polymers to protein 23: 1-28.
• Wang J, Wei Wang, Peter A Kollman, David A Case (2006) Automatic atom type and bond type perception in molecular mechanical calculations. Journal of molecular graphics and modelling 25(2): 247-260.
• Zhang Y, T S Lee, W Yang (1999) A pseudobond approach to combining quantum mechanical and molecular mechanical methods. The Journal of chemical physics 110(1): 46-54.
• Knegtel, R M, P D Grootenhuis (1998) Binding affinities and non-bonded interaction energies. Perspectives in drug discovery and design 9: 99-114.
• Bartell L S (1968) Molecular geometry: bonded versus nonbonded interactions. Journal of Chemical Education 45(12): 1-754.
• González M A (2011) Force fields and molecular dynamics simulations. École thématique de la Société Française de la Neutronique 12: 169-200.
• Krieger E, Tom Darden, Sander B Nabuurs, Alexei Finkelstein, Gert Vriend (2004) Making optimal use of empirical energy functions: force‐field parameterization in crystal space. Proteins 57(4): 678-683.
• Monticelli L, D P Tieleman (2013) Force fields for classical molecular dynamics, in Biomolecular simulations. Methods Mol Biol

 924: 197-213.

12. Cundari T R, Mark S.Gordon (1996) Effective core potential approaches to the chemistry of the heavier elements, Reviews in computational chemistry 147: 87-115.
13. Harder E, Wolfgang Damm, Jon Maple, Chuanjie Wu, Mark Reboul, et al. (2016 ) OPLS3: a force field providing broad coverage of drug-like small molecules and proteins. Journal of chemical theory and computation 12(1): 281-296.
14. Lopes P E, Jing Huang, Jihyun Shim, Yun Luo, Hui Li et al (2013) Polarizable force field for peptides and proteins based on the classical drude oscillator. Journal of chemical theory and computation 9(12): 5430-5449.
15. Poger D, A E Mark (2012) Lipid bilayers: The effect of force field on ordering and dynamics. Journal of chemical theory and computation 8(11): 4807-4817.
16. Klauda J B, Richard M Venable, J Alfredo Freites, Joseph W O Connor, Douglas J Tobias, et al. (2010) Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. The journal of physical chemistry B 114(23): 7830-7843.
17. Baker C M, V M Anisimov, A D MacKerell (2011) Development of CHARMM polarizable force field for nucleic acid bases based on the classical Drude oscillator model. The journal of physical chemistry B 115(3): 580-596.
18. Sim A Y, P Minary, M Levitt (2012) Modeling nucleic acids. Current opinion in structural biology 22(3): 273-278.
19. Vanommeslaeghe K, E Hatcher, C Acharya, S Kundu, S Zhong, et al. (2010) CHARMM general force field: A force field for drug‐like molecules compatible with the CHARMM all‐atom additive biological force fields. Journal of computational chemistry 31(4): 671-690.
20. Shih C J, Shangchao Lin, Michael S Strano, Daniel Blankschtein (2010) Understanding the stabilization of liquid-phase-exfoliated graphene in polar solvents: molecular dynamics simulations and kinetic theory of colloid aggregation. Journal of the American Chemical Society 132(41): 14638-14648.
21. Cornell W D, Piotr Cieplak, Christopher I Bayly, Ian R Gould, Kenneth M Merz, et al. (1995) A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. Journal of the American Chemical Society 117(19): 5179-5197.
22. Schmidt J M, Rafael Brueschweiler, Richard R Ernst, Roland L Dunbrack, Diane Joseph, et al. (1993) Molecular dynamics simulation of the proline conformational equilibrium and dynamics in antamanide using the CHARMM force field. Journal of the American Chemical Society 115(19): 8747-8756.
23. MacKerell A D, N Banavali, N Foloppe (2000) Development and current status of the CHARMM force field for nucleic acids. Biopolymers 56(4): 257-265.
24. Van Gunsteren, W F, X Daura, A E Mark (1998) Encyclopedia of Computational Chemistry. chapter GROMOS force field. NJohn Wiley and Sons.
25. Rappé A K, C J Casewit, K S Colwell, W A Goddard III, W M Skiff (1992) UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. Journal of the American chemical society 114(25): 10024-10035.
26. Halgren T A, (1996) Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94. Journal of computational chemistry 17(5‐6): 490-519.
27. Vanommeslaeghe K, AD MacKerell (2012) Automation of the CHARMM General Force Field (CGenFF) I: bond perception and atom typing. Journal of chemical information and modeling 52(12): 3144-3154.
28. Paton R S, J M Goodman (2009) Hydrogen bonding and π-stacking: How reliable are force fields? A critical evaluation of force field descriptions of nonbonded interactions. Journal of chemical information and modeling 49(4): 944-955.
29. Zhu H (2014) Implementation and Application of the MMFF94 Force Field.
30. Halgren T A, R B Nachbar (1996) Merck molecular force field. IV. Conformational energies and geometries for MMFF94. Journal of computational chemistry 17(5‐6): 587-615.
31. Bryantsev V S, B P Hay (2005) Using the MMFF94 model to predict structures and energies for hydrogen-bonded urea–anion complexes. Journal of Molecular Structure: THEOCHEM 725(1-3): 177-182.
32. Kaminski G, W L Jorgensen (1996) Performance of the AMBER94, MMFF94, and OPLS-AA force fields for modeling organic liquids. The Journal of Physical Chemistry 100(46): 18010-18013.
33. Barreiro E J, C R Rodrigues (1997) Molecular: uma ferramenta para o planejamento racional de fármacos em química medicinal. Química nova 20(3): 300-310.
34. Reges M, M M Marinho, E S Marinho (2018) In Silico Characterization of Hypoglycemic Agent Phenformin Using Classical Force Field MMFF94. International Journal of Recent Research and Review 11(2): 36-43.
35. Refaat H M, H A ElBadway, S M Morgan (2016) Molecular docking, geometrical structure, potentiometric and thermodynamic studies of moxifloxacin and its metal complexes. Journal of Molecular Liquids 220: 802-812.
36. El Wahab H A, M Abd El Fattah, Ayman H Ahmed, Ahmed A Elhenawy, N A Aliand (2015) Synthesis and characterization of some arylhydrazone ligand and its metal complexes and their potential application as flame retardant and antimicrobial additives in polyurethane for surface coating. Journal of Organometallic Chemistry 791: 99-106.
37. Cordomí A, G Caltabiano, L Pardo (2012) Membrane protein simulations using AMBER force field and Berger lipid parameters. Journal of chemical theory and computation 8(3): 948-958.
38. Dickson C J, L Rosso, Robin M Betz, Ross C Walker, Ian R Gould (2012) GAFFlipid: a General Amber Force Field for the accurate molecular dynamics simulation of phospholipid. Soft Matter 8(37): 9617-9627.
39. Krepl M, M Zgarbová, P Stadlbauer, Michal Otyepka, Pavel Banáš, et al. (2012) Reference simulations of noncanonical nucleic acids with different χ variants of the AMBER force field: quadruplex DNA, quadruplex RNA, and Z-DNA. Journal of chemical theory and computation 8(7): 2506-2520.
40. Stendardo E , Alfonso P, Paola C, Maria Cristina M, Orlando C, et al. ( 2010) Extension of the AMBER force-field for the study of large nitroxides in condensed phases: an ab initio parameterization. Physical Chemistry Chemical Physics 12(37): 11697-11709.
41. Pranata J, S G Wierschke, W L Jorgensen (1991) OPLS potential functions for nucleotide bases. Relative association constants of hydrogen-bonded base pairs in chloroform. Journal of the American Chemical Society 113(8): 2810-2819.
42. Kaminski G A, Richard A Friesner, Julian Tirado R, William L Jorgensen (2001) Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. The Journal of Physical Chemistry B 105(28): 6474-6487.
43. Pranata J, SG Wierschke, WL Jorgensen (1991) OPLS potential functions for nucleotide bases. Relative association constants of hydrogen-bonded base pairs in chloroform. J Ame Chem Soci 113(8): 2810-2819.
44. Kaminski GA, Richard A Friesner, Julian Tirado Rives, William L Jorgensen (2001) Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J Phys Chem 105(28): 6474-6487.
45. Price M L, D Ostrovsky, WL Jorgensen (2001) Gas‐phase and liquid‐state properties of esters, nitriles, and nitro compounds with the OPLS‐AA force field. J Comput Chem 22(13): 1340-1352.
46. Sakae Y, Y Okamoto (2010) Optimisation of OPLS–UA force-field parameters for protein systems using protein data bank. Molecu Simul 36(14): 1148-1156.
47. Shirley W I Siu, Kristyna Pluhackova, Rainer A Bockmann (2012) Optimization of the OPLS-AA force field for long hydrocarbons. J chem theory and comput 8(4): 1459-1470.
48. Par Bjelkmar, Per Larsson, Michel A Cuendet, Berk Hess, Erik Lindahl (2010) Implementation of the CHARMM force field in GROMACS: analysis of protein stability effects from correction maps, virtual interaction sites, and water models. J chem theory comput 6(2): 459-466.
49. Pastor R, A MacKerell Jr (2011) Development of the CHARMM force field for lipids. J phys chem lett 2(13): 1526-1532.
50. Momany FA, R Rone (1992) Validation of the general purpose QUANTA® 3.2/CHARMm® force field. J Comput Chem 13(7): 888-900.
51. Erwin S (1926) Quantisierung als Eigenwertproblem. Annalen der Physik 384(4): 361-376.
52. O Connor J J, E F Robertson (2017) Erwin Schrodinger and quantum wave mechanics. Quanta.
53. Schrodinger E (1995) The interpretation of quantum mechanics: Dublin seminars (1949-1955) and other unpublished essays. Ox Bow Pr.
54. Woolley RG (1991) Quantum chemistry beyond the Born-Oppenheimer approximation. Journal of Molecular Structure: THEOCHEM 230: 17-46.
55. Dalgarno A, G Victor (1966) The time-dependent coupled Hartree-Fock approximation. Proceedings of the Royal Society of London. Mathematical and Physical Sciences 291(1425): 291-295.
56. Helgaker T, P Jorgensen, J Olsen (2014) Molecular electronic-structure theory. John Wiley & Sons.
57. Parr R G, W Yang (1995) Density-functional theory of the electronic structure of molecules. Annu Rev Phys Chem 46(1): 701-728.
58. Michael P Allen, Dominic J Tildesley (2017) Computer simulation of liquids. Oxford university press.
59. Leach A R, A R Leach (2001) Molecular modelling: principles and applications. Pearson education.
60. Jensen F (1999) Introduction to Computational Chemistry. John Wiley & Sons, USA.
61. Hairer E, C Lubich, G Wanner (2003) Geometric numerical integration illustrated by the Störmer–Verlet method. Acta numerica 12: 399-450.
62. Rigling BD, R L Moses (2005) Taylor expansion of the differential range for monostatic SAR. IEEE Transactions on Aerospace and Electronic systems 41(1): 60-64.
63. Verlet L (1967) Computer" experiments" on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phy rev 159(1): 98.
64. Verlet L (1968) Computer" experiments" on classical fluids. ii. equilibrium correlation functions. Phy Rev 165(1): 201.
65. W F Van Gunsteren, H J Berendsen (1988) A leap-frog algorithm for stochastic dynamics. Molec Simu 1(3): 173-185.
66. S Toxvaerd (1991) Algorithms for canonical molecular dynamics simulations. Molec Phy 72(1): 159-168.
67. Allen M P (1982) Algorithms for Brownian dynamics. Molec Phy 47(3): 599-601.
68. Ciccotti G, J P Ryckaert (1986) Molecular dynamics simulation of rigid molecules. Comp Phy Rep 4(6): 346-392.
69. Nakajima N, H Nakamura, A Kidera (1997) Multicanonical ensemble generated by molecular dynamics simulation for enhanced conformational sampling of peptides. J Phy Chem B 101(5): 817-824.
70. Eslami H, F Muller Plathe (2007) Molecular dynamics simulation in the grand canonical ensemble. J compu chem 28(10): 1763-1773.
71. Berendsen HJ, J P M Postma, W F van Gunsteren, A DiNola, J R Haak, et al. (1984) Molecular dynamics with coupling to an external bath. J chem phy 81(8): 3684-3690.
72. Branka A, M Kowalik, K Wojciechowski (2003) Generalization of the Nosé–Hoover approach. The Journal of chemical physics 119(4): 1929-1936.
73. Okumura H, Y Okamoto (2004) Molecular dynamics simulations in the multibaric–multithermal ensemble. Chemical physics letters 391(4-6): 248-253.
74. Tian P (2008) Molecular dynamics simulations of nanoparticles. Annual Reports Section" C"(Physical Chemistry) 104: 142-164.
75. Sohraby F, Mojtaba Hadi Soltanabad, Milad Bagheri, Masood Bezi Javan, Mostafa Javaheri Moghadam, et al. (2020) Application of Molecular Dynamics in Coating Ag-Conjugated Nanoparticles with Potential Therapeutic Applications. Nano Biomed Eng 12(1): 90-98.
76. Blazhynska M M, A Kyrychenko, O N Kalugin (2018) Molecular dynamics simulation of the size-dependent morphological stability of cubic shape silver nanoparticles. Molec Simu 44(12): 981-991.
77. Blazhynska M M, AV Kyrychenko, O N Kalugin (2019) Polarizable force field for molecular dynamics simulations of silver nanoparticles. VN Karazin Kharkiv National University Bulletin. Chemical series (32): 46-58.
78. Alarifi H, M. Atis, C Ozdogans, A Hu, M Yavuz, et al. (2013) Determination of complete melting and surface premelting points of silver nanoparticles by molecular dynamics simulation. J Phys Chem C 117(23): 12289-12298.
79. HA A, M Atis, C Özdoğan, A Hu, M Yavuz, et al. (2013) Molecular dynamics simulation of sintering and surface premelting of silver nanoparticles. Materials Transactions 54(6): 884-889.
80. Chen L, Q Wang, L Xiong (2017) Molecular dynamics study on structure stability, lattice variation, and melting behavior of silver nanoparticles. J Nanoparticle Research 19(9): 300.
81. Martin P, Peng Zhang, P Mark Rodger, Eugenia Valsami Jones (2019) Simulations of morphological transformation in silver nanoparticles as a tool for assessing their reactivity and potential toxicity. Nanoimpact 14: 100147.
82. Ashrafali Mohamed Ismail, Om Prakash Sharma, Muthuvel Suresh Kumar, Chundamanil Eapen Eapen, Rajesh Kannangai, et al. (2013) Virological response and antiviral resistance mutations in chronic hepatitis B subjects experiencing entecavir therapy: an Indian subcontinent perspective. Antiviral research 98(2): 209-216.
83. Dante Morgnanesi, Eric J Heinrichs, Anthony R Mele, Sean Wilkinson, Suzanne Zhouet al. (2015) A computational chemistry perspective on the current status and future direction of hepatitis B antiviral drug discovery. Antiviral res 123: 204-215.
84. Alfan Danny Arbianto, Firdayani, Susi Kusumaningrum, Raodatul Jannah, Puspa Dewi N Lotulung, et al. (2018) Computational Studies and Molecular Dynamic Simulation to Design Lead Compounds for Hepatitis B Virus. J Young Pharmacists 10(2s): S148-S152.
85. L L Fu, J Liu, Y Chen, F T Wang, X Wen, et al. (2014) In silico analysis and experimental validation of azelastine hydrochloride (N4) targeting sodium taurocholate co‐transporting polypeptide (NTCP) in HBV therapy. Cell prolif 47(4): 326-335.