The Use of Multilayer Mesh Electrically Conductive Nanotubes Taking into Account Chirality in Damaged Active and Inactive Neural Networks

Neural Networks

The mammalian brain is made up of different areas that perform different tasks. The cortex is the outer layer of the mammalian brain. We can think of it as a thin sheet (2 to 5 mm thick) that folds on its own to increase its surface area. The cerebral cortex is the largest and most developed part of the human brain. It contains a large number of nerve cells, neurons. The human cortex contains about 1010 neurons. They are connected by nerve threads (axons) that branch out and end in synapses. These synapses are connections to other neurons. Synapses connect to dendrites, branched extensions of the body of a nerve cell designed to receive input signals from other neurons in the form of electrical signals. A neuron in the human brain can have thousands of synaptic connections to other neurons. The resulting network of connected neurons in the cortex is responsible for processing visual, audio, and sensory data. (Figure 1) Neurons in the cerebral cortex (the outer layer of the brain, the largest and most developed part of the human and mammalian brain). (Figure 2) shows a more schematic view of the neuron. The information is processed from left to right. On the left are the dendrites that receive the signals and connect to the cell body of the neuron, where the signal is processed. The right part of the picture shows the axon through which the output is directed to the dendrites of other neurons. The information is transmitted as an electrical signal. The information is transmitted as an electrical signal (Figure 3) shows a Schwann cell, which can be in a neutral state and create a left positive or right negative chirality on the axon. (Figure 4) shows an example of the time series of the electric potential of a pyramidal neuron [5]. The time series consists of an intermittent series of electric potential jumps. Periods of rest without spikes occur when the neuron is inactive, and during periods rich in spikes, the neuron is active. (Figure 4D) Temporary portraits of the system (1) (Figure 5).

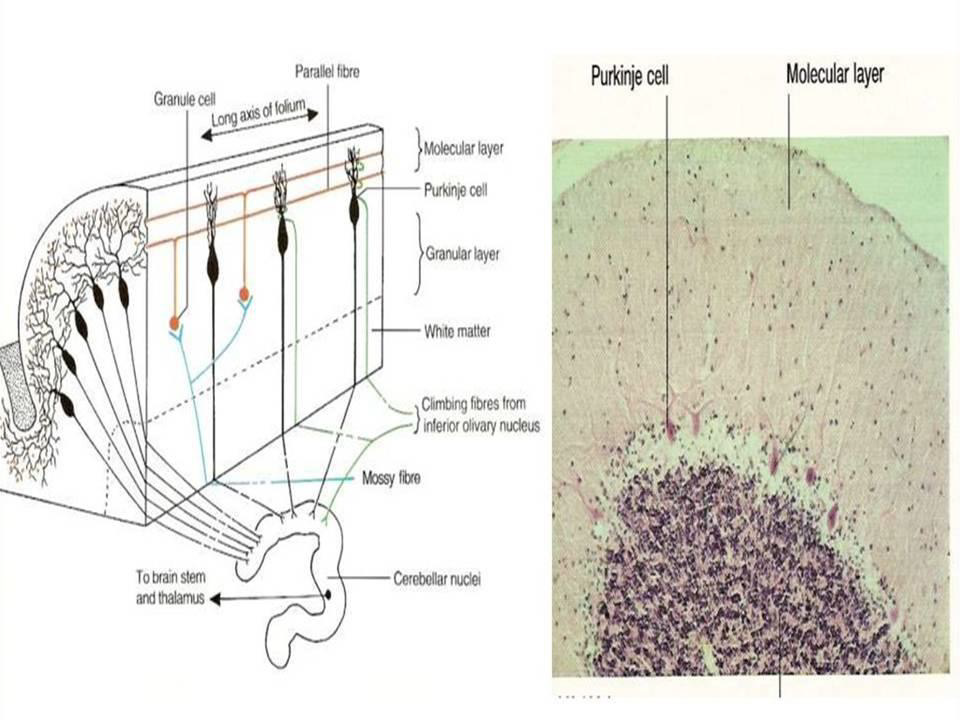
Figure 1: Neurons in the cerebral cortex (the outer layer of the brain, the largest and most developed part of the human and mammalian brain).

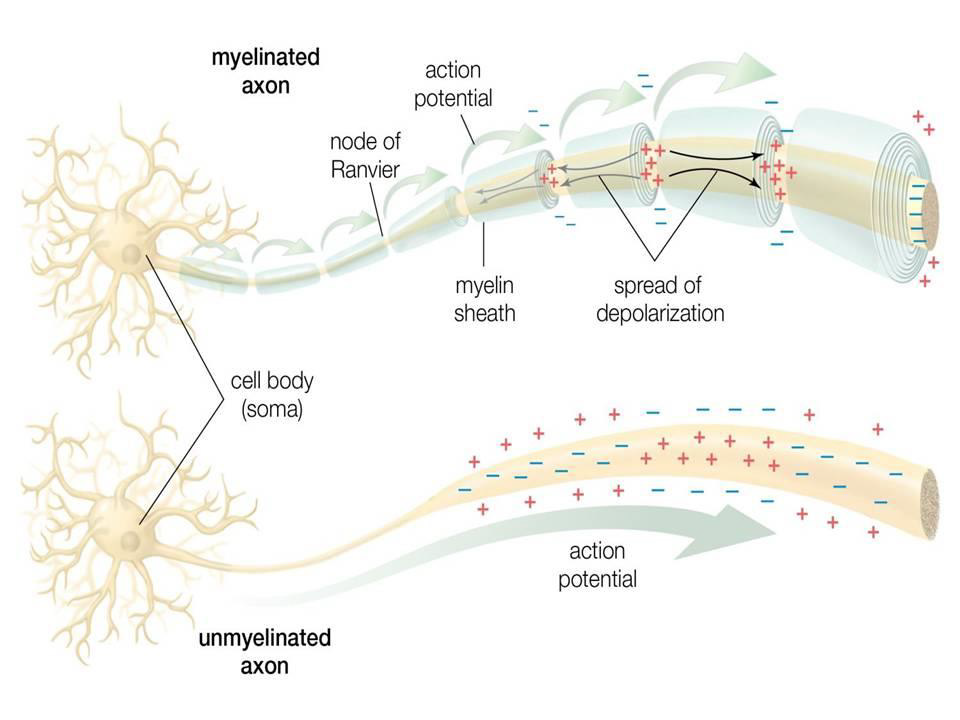
Figure 2: Schematic representation of a neuron. Dendrites receive input signals in the form of electrical signals through synapses. The signals are processed in the cell body of the neuron. The output signal is transmitted from the body of the nerve cell to other neurons via the axon.

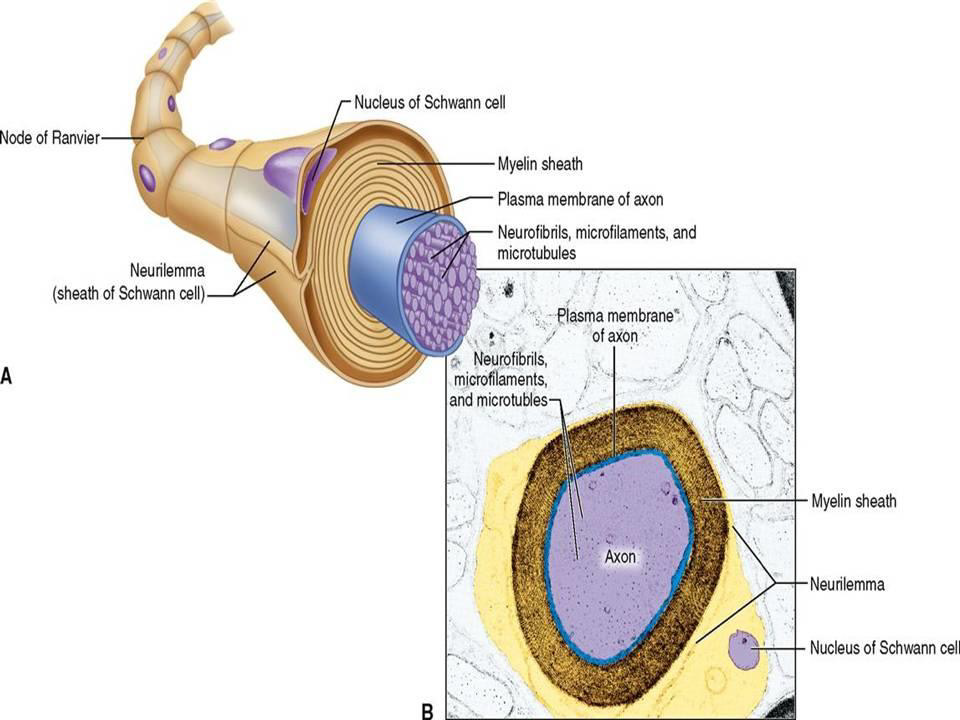
Figure 3: Shows a Schwann cell, which can be in a neutral state and create a left positive or right negative chirality on the axon.

Figure 4: Shows an example of the time series of the electric potential of a pyramidal neuron. The time series consists of an intermittent series of electric potential jumps.

Figure 5: a) armchair, b) zigzag, c) chiral, d) multi-layer.

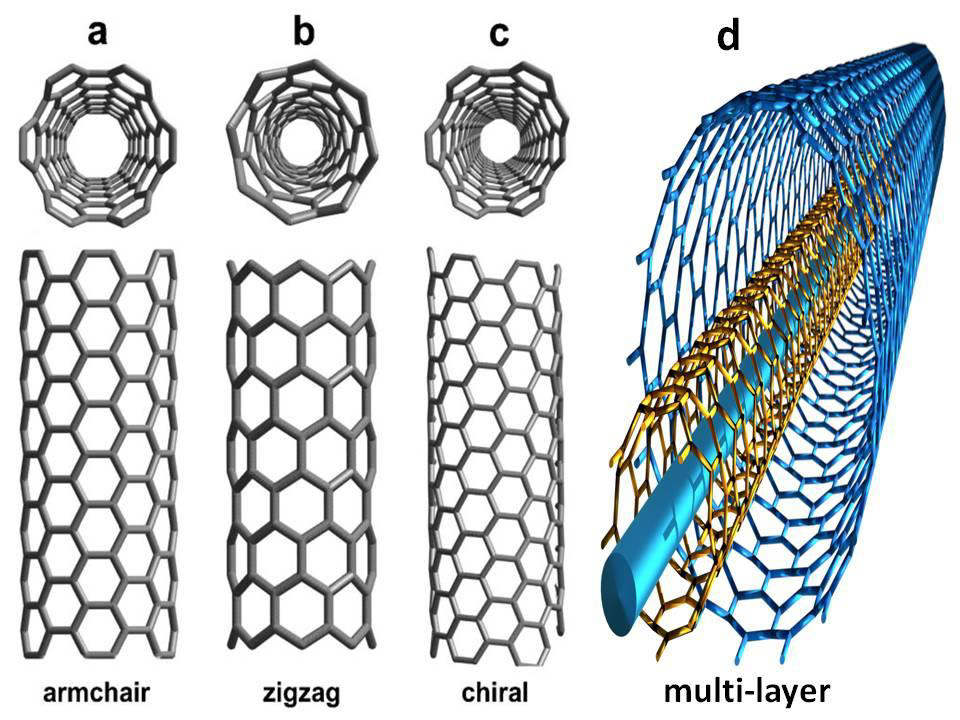
Mesh Nanotubes

The mathematical dynamic model of the soliton

The mathematical dynamic model of the soliton is represented by the equation (1) [6,7].

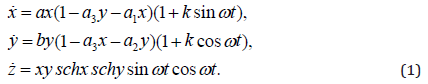
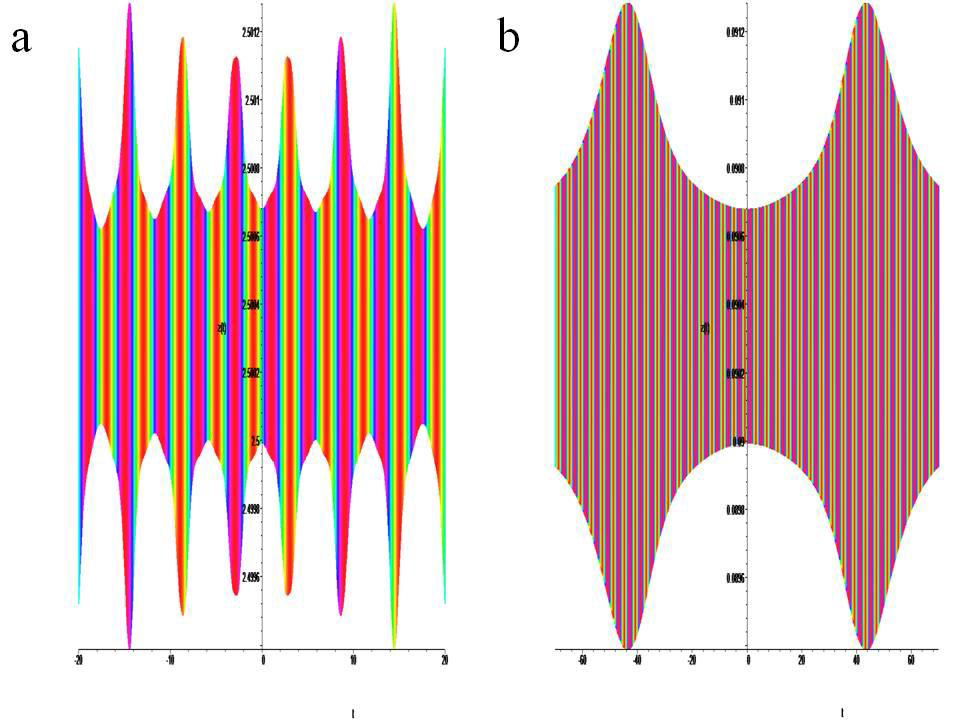
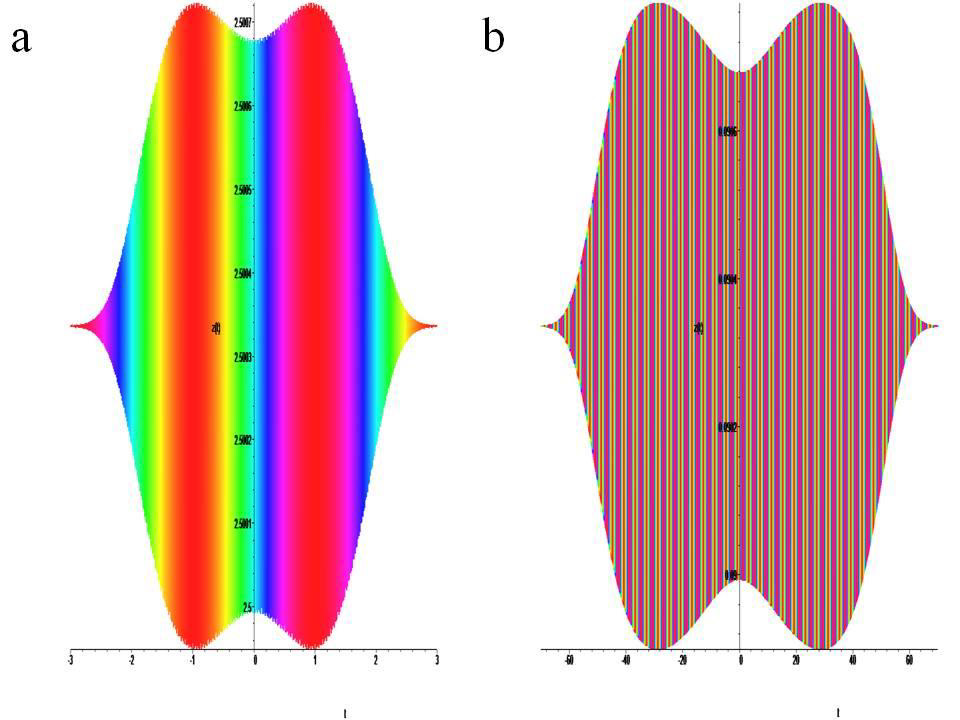
Time portraits of the system (1) are shown in (Figure6a) active with positive

a =1.0, a₁ = 0.2, a₂ = 0.1, a₃ = 1.0, b = –2.0, k = 0.045, ω = 64π and negative a =–1.0, a₁ = 0.2, a₂ = –0.1, a₃ = 1.0, b = 2.0, k = 0.045, ω = 64π chirality. (Figure 6b) passive positive a =0.09, a₁ = 0.2, a₂ =0.1, a₃ = 1.0, b = –0.09, k = 0.045, ω = 64π and negative a =–0.09, a₁ = 0.2, a₂ = –0.1, a₃ = 1.0, b = 0.09, k = 0.045, ω = 64π chirality: Time portraits of the system (1) are shown in (Figure 7a) active with positive a =1.0, a₁ = 0.2, a₂ = 0.1, a₃ = 1.0, b = 2.0, k = 0.045, ω = 64π and negative a =–1.0, a₁ = 0.2, a₂ = –0.1, a₃ = 1.0, b = –2.0, k = 0.045, ω = 64π lack of chirality. (Figure 7b) passive positive a =0.09, a₁ = 0.2, a₂ =0.1, a₃ = 1.0, b = 0.09, k = 0.045, ω = 64π and negative a =–0.09, a₁ = 0.2, a₂ = –0.1, a₃ = 1.0, b =– 0.09, k = 0.045, ω = 64π lack of chirality:

Figure 6: Temporary portraits of the system with chirality. (1) at : a) x₀ = 0.4, y₀ = 0.4, z₀ = 2.5, b) x₀ = 0.4, y₀ = 0.4, z₀ = 0.09.

Figure 7: Temporary portraits of the system with no chirality. (1) at : a) x₀ = 0.4, y₀ = 0.4, z₀ = 2.5, b) x₀ = 0.4, y₀ = 0.4, z₀ = 0.09.

Summary

Artificial neural networks use a highly simplified model for the fundamental computing unit-the neuron. In its simplest form, the model is simply a binary threshold unit. The network performs these calculations sequentially. Usually, discrete sequences of calculation time steps are considered, t = 0,1,2,3.... Either all neurons are updated simultaneously at one time step (synchronous update), or only one selected neuron is updated (asynchronous update) [8-19]. We proposed a different approach to use the wave-soliton approach, taking into account chirality. In the presence of different chirality, three states are possible, with positive chirality, the signal is transmitted without loss, with negative chirality, the signal creates pulsations in certain parts of the axon. In the absence of a signal, a chaotic self-excitation is observed in the axon. A run a way with no chirality exists for a short time and represents a stop signal. The conclusion is that the soliton model can be used to study the behavior of an individual axon , and the damaged sections of axons can be replaced by multilayer mesh electro-conducting nanotubes.

References

• Sergey Belyakin, Sergey Shuteev (2020) Analysis of dynamics of infected active and uninfected active populations leading to pandemics using a discrete model of two interacting pacemakers taking into account the time of refractoriness. Journal of Nanosciences Research & Reports.
• Belyakin ST, Shuteev SA The generalized model N - pacemaker curve phase response of the Atria, ventricular fibliration and AB - blockade. Global Journal of Nanomedicine.
• Belyakin ST, Shuteev SA Application of sampling methods to nanostructures on the example of cellular structures of cardiac arrhythmia dynamics. Advances in Nanoscience and Nanotechnology journal.
• Lecun A, Bengio Y, Hinton G Deep learning. Nature.
• Gabbiani, F, Metzner W (1999) Encoding and processing of sensory information in neuronal spike trains. Journal of Experimental Biology 202(10): 1267-1279.
• Belyakin ST, Shuteev SA (2021) Classical soliton theory for studying the dynamics and evolution of cylindrical shock waves in passive dispersed and active relaxation media. Journal of Applied Material Science & Engineering Research.
• Belyakin ST, Shuteev SA Study of the dynamics and evolution of fibrillation in the human heart by the classical soliton model. Journal of Cardiology Interventions.
• Borg-Graham L (1998) Interpretations of data and mechanisms for hippocampal pyramidal cell models. In: Cerebral Cortex. Plenum Press.
• Chizhov AV, Graham LJ (2007) Population model of hippocampal pyramidal neurons, linking a refractory density approach to conductance-based neurons. Phys Rev E 75(1 Pt 1): 011924.
• Chizhov AV, Graham LJ (2008) Efficient evaluation of neuron populations receiving colorednoise current based on a refractory density method. Phys Rev E 77(1 Pt 1): 011910.
• Chizhov AV, Rodrigues S, Terry JR (2007) A comparative analysis of a firing-rate model and a conductance-based neural population model. Physics Letters A 31-36.
• Cruikshank SJ, Lewis TJ, Connors BW (2007) Synaptic basis for intense thalamocortical activation of feedforward inhibitory cells in neocortex. Nature Neuroscience 462-468.
• Eggert J., van Hemmen J.L., (2001) Modeling Neuronal Assemblies: Theory and Implementation. Neural Computation.
• Gerstner W, Kistler WM, (2002) Spiking Neuron Models, Single Neurons, Populations, Plasticity. Cambridge University Press.
• Kandel ER, Schwartz JH, Jessell TM (2000) "Principles of Neural Science. Fourth edition".
• Karnup S, Stelzer A, (1999) Temporal overlap of excitatory and inhibitory afferent input in guineapig CA1 pyramidal cells. J.Physiology, 516(Pt 2): 485-504.
• Kopell N, Ermentrout GB, Whittington MA, Traub RD (2000) Gamma rhythms and beta rhythms have different synchronization properties. Neurobiology 97(4): 1867-1872.
• Nykamp D, Tranchina D (2000) A Population Density Approach That Facilitates Large-Scale Modeling of Neural Networks: Analysis and an Application to Orientation Tuning. J. Comput. Neuroscience 19-50.
• Omurtag A, Knight BW, Sirovich L (2000) On the simulation of large populations of neurons. J Comput Neuroscience 51-63.