The Importance of Catastrophe Theory and Nonlinear Modeling Applied to the Collapse of Afghanistan in the Late Summer of 2021

Introduction

Statistics classes can be challenging both emotionally and intellectually for undergraduate students. The senior author experienced this in the fall of 1970, when as a junior at the College of William and Mary (Virginia), his statistics professor told his students on the first day of class that he would fail at least 75% of the class because he didn’t want to teach classes of more than ten students (42 had enrolled). When the senior author had attained an average of 35%, which was above the class average of 22%, he was offered a “C” grade if he would promise to never enroll in another course with the professor, which led to his taking a course in law in the spring of 1971. Such situations tend to intimidate students, especially with respect to STEM courses. One way to overcome anxiety about STEM courses is to use ancient or recent historical events for statistical testing. If students are shown practical examples of the use of statistics regarding important past or current events, learning may be facilitated. Along the way it may be possible for students to co-publish such tests, establishing a publication record prior to attending graduate school. Recent articles that have combined history with statistical testing have concerned the space shuttle Challenger disaster, the loss of the RMS Titanic, and the attack on Pearl Harbor in December 1941 [1], the sinking of the Sewol [2], arrow wounds prior to the U.S. Civil War as well as ancient documents [3], and the early history of Islam [4,5].

Literature Review

A very recent example that combined history with the use of statistics in a fall 2021 basic statistics class in a midwestern United States community college was the use of statistics to predict the fall of the government of Afghanistan and the rise of the Taliban in the summer of 2021. The United States’ role in Afghanistan has not been without controversy. Some leaders wanted to maintain a presence in Afghanistan, even if at reduced levels, while others wanted us to entirely withdraw our military forces [6,7]. Some thought that if U.S. military forces were withdrawn, the Afghanistan government would collapse, or that, at least, collapse would be a possibility, while others were not sure if that would happen [7]. It was possible that withdrawal from Afghanistan might allow the United States to better focus on strategic goals in other regions, especially areas threatened by China [6,7]. Since 1960, there have been at least 15 cases of state collapse, as detailed by Johais, Bayer, & Lambach [8]. With reference to Afghanistan, it was recognized by the spring of 2020 that “It will take urgent efforts to prevent the collapse of Afghanistan” (9, p. 142) and by February 2021 that there was a strong possibility that the Taliban might overthrow the Afghan government unless the U.S. continued to provide political and military support [9]. Some attributed the crisis of the COVID-19 epidemic as a factor in weakening U.S. resolve to remain in Afghanistan [9, p. 141].

Relevance for Public Health

Collapse of state governments can create serious humanitarian emergencies. Rubin [8,9], fearing a collapse of Afghanistan, was concerned about the consequences for humanitarian reasons, especially with respect to public health. Britten and Amer [10] feared that without continued funding of health care systems in Afghanistan from overseas, their health service which had grown to support 90% of Afghanistan’s population [11] might collapse. The replacement of the minister of public health with an official untrained in health services was seen as a bad omen [10]. A recent report alleges that “Afghanistan will face its worst famine in 35 years” with “roughly 23 million of the 38 million population…. already facing food insecurity so grave they do not know where their next meal will come from” and that “95% of Afghans don’t have enough food” [12]. Poor nutrition and famine might well precede even greater public health disasters. Many wondered if it had to end in the way it did. “How had two decades of blood and treasure left a porous apparatus either unwilling or unable to defend itself?” [14, p. 108]. However, it appears that “Few had predicted how quickly Kabul would fall and how rapidly the Afghan military forces would collapse” [6, p. 1). That raised the questions of [1] whether the timing of the fall of Afghanistan could have been predicted statistically from open source data, [2] if so, why did the fall seem to occur so unexpectedly and [3] could anyone have done a more accurate job of predicting the fall?

On July 8th, President Biden stated in public at a news conference that Afghanistan was no where near falling to the Taliban. Many may not know that there were data available at that time to use to predict when Afghanistan might fall. One could use linear and nonlinear (quadratic) models to predict when it might fall. Furthermore, catastrophe theory could have been used to consider the possibility of a rapid collapse after a critical mass was met or a critical event occurred. Such a critical event might have been the abandonment of Bagram Air Base on July 2/3. Once Afghan soldiers realized “no more air support, no more Army/Marine support, no communications support, no more intelligence support” they may have felt abandoned, too. Their morale may have crashed. With respect to public health, the ability to more accurately predict the collapse of a regime would be useful for maintaining public health services, maintaining the health and safety of public health personnel, and reducing health-related consequences associated with a collapse of government and related government services, including public health services.

Theory

A theory that may have been overlooked with respect to predicting the fall of Afghanistan - for example, it was overlooked in a study [8] of the collapse of 15 nations’ governments – is catastrophe theory [13]. In its full form, catastrophe theory predicts disaster as a three-dimensional situation in which an interaction effect among two independent variables leads to disaster in some situations but not others, depending on change in one of the two independent variables [14,15]. However, our approach was less complex, predicting disaster (i.e., fall to the Taliban) as a function of the number of provinces under government vs. Taliban control over time, from April to August 2021. Our model was two-dimensional but still related to catastrophe theory in that it was potentially capable of predicting a sudden fall of Afghanistan or a much slower decline in government control. Catastrophe theory might predict an earlier collapse of the Government and takeover by the Taliban, which could be tested using a nonlinear (i.e., quadratic) statistical model, which could explain more variance than linear models. Furthermore, if the fall of Afghanistan was more rapid than could be modeled statistically, that by itself might provide support for catastrophe theory, as a theory capable of explaining changes more rapid than what might be expected statistically, using any form of linear or nonlinear models.

Research Questions

a) Linear Model: Could the fall of Afghanistan have been predicted by a linear ordinary least squares regression analysis of the time from April 2, 2021, forward from the growing number of provinces controlled by either the Taliban or the Government?

b) Nonlinear Models: Could the accuracy of the timing of the fall of Afghanistan have been predicted more accurately using nonlinear models?

c) Difference Between Linear and Nonlinear Models: Would the difference between linear and nonlinear models be significantly different by statistical testing?

Would the fall of Afghanistan occur more rapidly than predicted by the best linear or nonlinear models? If so, that result might lend more support to catastrophe theory.

Methods

Data

Data were obtained from open sources, including the website for the Long War Journal [16] and an article published by Reuters [17]. For certain dates after April 1, 2021, reports were available on the number of provinces in Afghanistan controlled by the Taliban or the Government as well as those contested between the Taliban and the Government. We also developed a measure that was the sum of the number of the contested and the Taliban-controlled provinces. The predictor variable was time, expressed as the number of days since April 2, 2021. The data are presented in Table 1.s

Table 1: Kampo compositions of Kakkonto, Shosaikotokakikyosekko, Saikatsugekito, Kakkontokasenkyushin’I, and Hochuekkito.

Analyses

We used the regression curvefit program in SPSS [18] to predict linear and quadratic models for the predicted dates of the fall of Afghanistan. Since the Taliban would consider taking over 400 provinces as victory, we calculated that date (of collapse) by substracting 400 from the constant obtained and solving the quadratic equation using https://www.calculatorsoup.com/ calculators/algebra/quadratic-formula-calculator.php website with ax2+bx+c = 0. Since the government would be deemed fallen when its provinces under control reached zero, we solved our quadratic equations for zero for the government predictions. In three cases, the quadratic equations did not have solutions because the quadratic curve did not reach zero (government) or 400 (Taliban); in such cases we recommend using the linear model.

We also used a quality control model [20, p. 277] to detect significant changes in Taliban and government control. Control models were invented in the 1920’s as warning devices; times do not have to be equally spaced and normal distributions are not necessary for them to be useful [19]. The general principle is that if there are no significant changes over time, then it will be very rare to see deviations of two or three standard deviations from the mean. Up to but not including June 23, the mean score for the number of districts controlled by the Taliban was 86.5 (SD=9.58). A control model would put demarcations at plus two or three standard deviations, that being 106 and 115 districts under their control. If the total under Taliban control reached 115 that would be a type I “out of control” signal; if the total featured two or three adjacent dates being 106 or greater, that would be a type III “out of control” signal; if nine or more in a row were above 92, that would be a type II “out of control” signal. However, because the changes were generally monotonic, the first day at two or three standard deviations would probably have meant more than one adjacent day at that level, so for our purposes the first day at two or three standard deviations would be a valid “signal”. For the government the mean score was 109.88 (SD = 16.13) with 78 districts representing a loss of two standard deviations and 61 districts representing a loss of three standard deviations.

Results

Linear Models

Almost all of the linear models were statistically significant, which would probably have led analysts to believe that they were accurate and sufficient. On one hand, none predicted the fall before late September; on the other hand, they all predicted a fall at some point in the future. There would seem to have been greater certainty of the fall rather than regarding the precise timing of the fall. We have 12 predictions about the fall of Afghanistan by linear modeling (Table 2). The earliest predicted date would be October 25, the latest would be September 25, 2022. The average of the 11 earlier dates would be November 24 while the median would be November 16 with SD = 21.96, making plus or minus 2SD from September 29 to January 6, 2022. The SE of the Mean was 6.62 days. If we add in the latest predicted date, the average would be December 19 while the median would be November 19, with an SD of 90.53; two SD below the average would be June 21 while two SD above was June 18, 2020. The SE of the mean was 26.13. As of late June, linear modeling would have predicted the fall of Afghanistan in mid-November, excluding the one outlier date. As of late July, linear modeling would have predicted sometime in November, perhaps as late as the first week of December. Even about the time it fell to the Taliban, linear modeling would have predicted late October to late December. The predictions of linear modeling were relatively consistent in that they failed to predict the fall in mid- August, missing that date by at least two to three months.

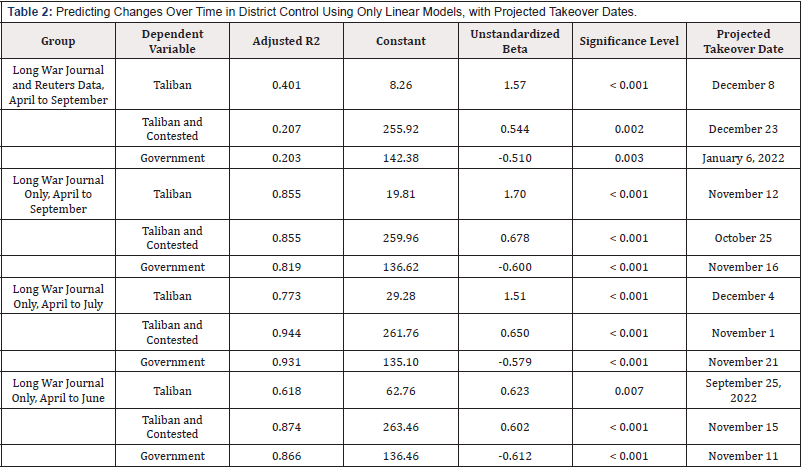
Table 2: Predicting Changes Over Time in District Control Using Only Linear Models, with Projected Takeover Dates.

Nonlinear Results

Quadratic modeling (Table 3) would have predicted the fall of Afghanistan between August 28th and October 25th, excluding an outlier for May 27, 2022. (Figure 1) illustrates the linear, quadratic, and exponential models for the combined Long War Journal data and the Reuters data for the entire time frame from April through August 2021 predicting increasing Taliban control of districts; (Figure 2) illustrates the linear and quadratic models from the same data for declining government control of districts over time. (Figure 3) illustrates the linear, quadratic, and exponential results for Long War Journal data as of the end of June for increasing Taliban control (as a control against “hindsight” bias or error).

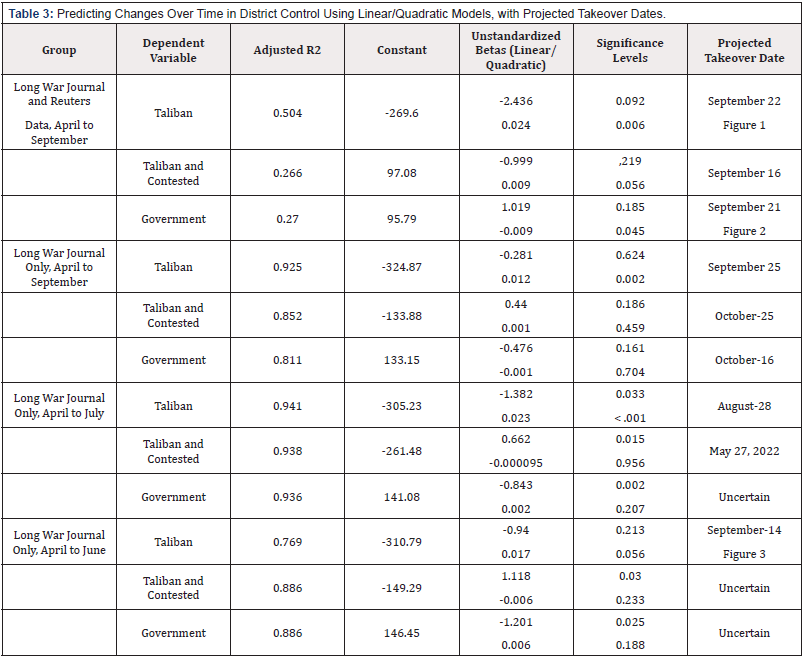
Table 3: Predicting Changes Over Time in District Control Using Only Linear Models, with Projected Takeover Dates.

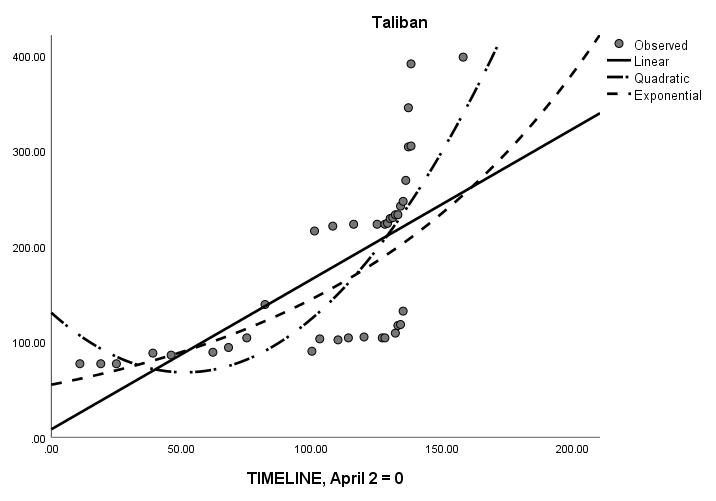
Figure 1: Linear, Quadratic, and Exponential Modeling of the Fall of Afghanistan Using Data from April to August 2021.

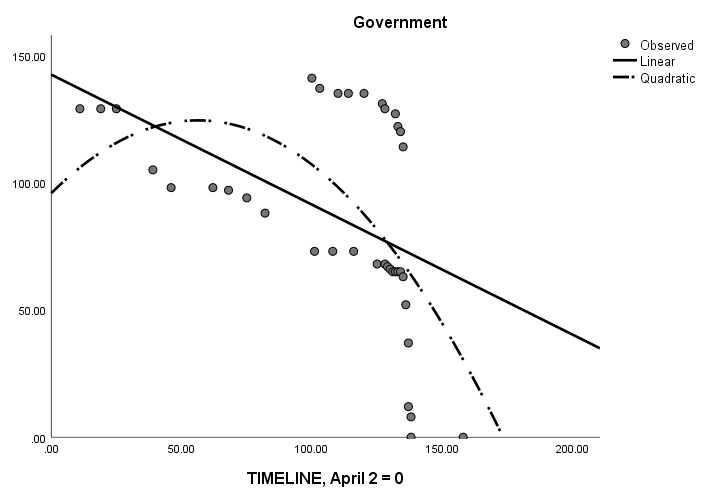
Figure 2: Linear and Quadratic Modeling of the Fall of Afghanistan Using Data from April to August 2021.

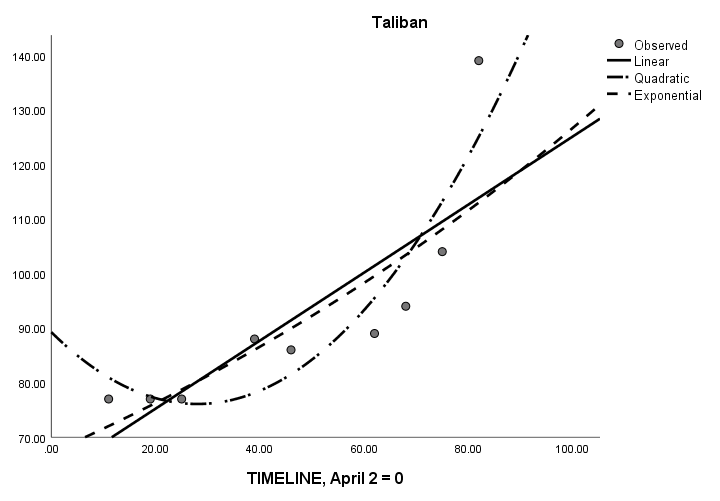
Figure 3: Linear, Quadratic, and Exponential Modeling of the Fall of Afghanistan Using Data as of the 23rd of June 2021.

Comparing Results for Linear and Nonlinear Models

Initially we compared the results for linear versus quadratic modeling with a paired samples t-test, but the assumption of a positive correlation between the items was not met, so we changed to an independent samples t-test, followed by nonparametric Mann-Whitney U tests (both of which tests compare independent samples), since neither the total group (N = 24) nor the subgroups for linear and for quadratic data featured normally distributed results (one sample Kolmogorov-Smirnov tests, all results rejected the normal hypothesis, p<.005). Where quadratic predictions were not available, we substituted the linear predictions for our first analysis. Thus, we had an average date of December 19 (Mean = 261.33, SD = 90.53 days) for the linear model and October 28 (Mean = 209.58, SD = 71.61 days) for the quadratic model. However, that difference was not statistically significant (t [22] = 1.55, p = .135), although if you assumed the quadratic method was better, you could use a one-tailed test and reduce p to < .07, possibly a trend worth noting. The effect size was d = 0.63, a medium or larger effect size [20]. However, the U test = 25.0, with z = 2.72, p = .007. Since the data used were not normally distributed, the nonparametric results should be deemed more likely to be accurate. However, we redid the analysis after removing the largest outlier in each group; then we had an average data of November 24 (Mean = 235.91, SD = 21.96 days) for the linear modeling compared to October 8 (Mean = 190.45, SD = 28.48 days) for the quadratic modeling. For this comparison t (20) = 4.19 (p < .001, two-tailed), a significant result, with a very large effect size of d = 1.79. Cohen [21] stated that an effect size of 0.80 or larger could be considered “large”. A Mann- Whitney U test yielded z = 3.06, p = .002.

We performed a third set of analyses, deleting the quadratic results that could not be solved, rather than replacing them with the linear results. We found an average date of November 24 (Mean = 235.91, SD = 21.96, as before) for the linear method with an average date of September 24/25 (Mean = 176.50, SD = 18.32, N=8 for the quadratic modeling). For this comparison, t(17) = 6.22, p < .001 with an effect size, d = 2.94. The Mann-Whitney U test yielded z = 3.59, p < .001. While these results may seem to indicate less than complete support for our comparison of linear and nonlinear models, one must consider the dangers of type II error as well as as type 1 error. If you think that the linear model is correct and expect Afghanistan to fall late in the autumn of 2021 but it occurs in August, you would look like your predictions were very poor, that you were taken by surprise, which could be seen as an embarrassment to those who used only a linear model. In addition, there would be many practical problems created by a “premature” collapse of the Afghan government.

If your prediction had proved correct by the linear model, one would have been into the deep of winter, a time when fighting would be a challenge for both sides in the conflict, a time when not much “action” might occur and the situation might be a stalemate politically and militarily. Overall, the risks of an earlier-thanexpected collapse would seem to outweigh the risks of a later expected collapse, especially in terms of threats to the health care system associated with an unexpected, earlier collapse. Furthermore, the effect sizes for our comparisons ranged between 0.63 and 2.94, in the medium to very large range, not something to trifle with, as Cohen’s [20] interpretation of an effect size of less than ours, d = 0.50, would be something observable to the naked eye (i.e., of practical value). Furthermore, the results from our nonparametric tests were consistently very significant (p < .01) and those tests did not require an assumption of normally distributed data, which was not met with the data we used.

Avoiding “Hindsight” Bias

Limiting our analyses to time periods including April through May and April through June, we found predicted dates of collapse from August to mid-November 2021. Some calculations were uncertain and did not predict collapse (the quadratic equations could not be solved). In other words, had the models been tested one to two months before the collapse, given the available data, nonlinear models would still have predicted an earlier collapse than linear models.

Quality Control Models

With respect to growing Taliban control, plus two standard deviations occurred by June 23; plus three standard deviations occurred on July 10. With respect to declining government control, minus two standard deviations were met on July 10 but minus three standard deviations were not met until August 14. Nevertheless, both approaches feature July 10 as a key turning point in changing control between the Taliban and the government of Afghanistan. The results indicate that problems with unusually high gains for the Taliban and unusually high losses for the government should have been statistically detectable by July 10, not long after President Biden’s speech on July 8.

Catastrophe Theory

None of the linear or nonlinear models tested predicted the fall of Afghanistan in mid-August. That result supports the need to consider catastrophe theory when evaluating potentially volatile situations. Under some conditions, things can fall apart very quickly, more quickly than might be expected. History is replete with such examples. Normalcy bias (apres moi le deluge) may lead a person or a group to believe that things will always continue the same as they always have in the past or at least, the recent past. Things will never change until I am gone. Catastrophe theory may be an antidote to such normalcy bias. There are other theories about the decline of more complex societies, especially with respect to Western nations [21] versus the rise of China, but our focus here is strictly on the fall of Afghanistan.

Teaching Points

As this project was part of the basic statistics class, it featured lessons beyond the specifics of this set of data and the particular analyses conducted. There were several teaching points made during the class that related to this project and beyond. The first teaching point was that developing an idea to check out is the most important part of the research process. No idea, no results! There are many very intelligent people with few new ideas. If you can develop a new idea to test, you can, if you need to do so, hire others to work out the details and apply the statistics. Developing new ideas takes creativity, which may be a different form of intelligence than that captured by simple IQ tests.

A second teaching point concerns the importance of valid data. Getting valid data may often be the most difficult part of research. In this case, the data from Reuters didn’t match that from the Long War Journal. Because the Long War Journal featured data over a longer time period, we focused on that source of data. However, because of the data mismatch and the totals of the provinces varying between Reuters and the Long War Journal, data is one of the limitations of this analysis. At one point, it was discovered that our data set had two errors, which we had to correct; we had to redo the analyses, of course. Furthermore, if everything else is equal, if you have a choice of data sets, you probably want to select the set that has more data, as that will allow for more detailed statistical testing.

At the same time, if the smaller data set is of higher quality, you may have to sacrifice some of the depth of your statistical testing. Another data issue illustrated here is that data may be ambiguous. For example, a question might be answered, yes, no, or not sure. How the” not sure” answers are coded could make a substantial difference in the results of analyses. In this case, the “contested” provinces are ambiguous in their status. Does “contested” mean that the Taliban had control of 10% of the province or does it mean that the Taliban had 90% control, except for the capital town of the province? Our data sources were not clear on that issue although we believe the latter was intended.

A third teaching point is that many scholars limit themselves to testing linear models, i.e., straight lines. However, life is often nonlinear, usually that being quadratic. The ancient Greek idea of the golden mean, if valid, suggests that some aspects of life will feature a quadratic model. A classic example is blood pressure - too low or too high are both dangerous, while a balanced level is best. There are several possible nonlinear patterns; the SPSS curve estimation program under the REGRESSION program allows for testing of a several nonlinear patterns and provides relative estimates of the ability of each to fit the data provided. In this example, a quadratic model often worked better than other models, including the exponential model. The point being that if one limits oneself to testing only linear models, then one may make some serious errors of prediction.

A fourth teaching point is that any problem may be considered from a variety of theoretical perspectives. Even if you have a favorite theory or theoretical framework, there may be situations in which your favorite theory does not work as well at suggesting hypotheses as would a different theory. Just as it is unwise to consider only linear models, it is unwise to limit oneself to only one theory. For any problem, it is likely that more than one theory might be relevant and useful. In this case, catastrophe theory seemed relevant, even though it was probably overlooked by many scholars.

A fifth teaching point is that after the fact, analyses may fit the data by chance. One could contest our research by saying that fitting the data after the fall of Afghanistan is like predicting that the murder victim is dead after being found deceased by the police. Nor does statistically controlling for the impact of bullets on the deceased victim bring them back to life. Fitting data to a model after the fact does not help prevent the undesired outcome, indeed. That is why we modeled our data from points in May or June (Figure 3) in order to see if the fall could have been more accurately predicted months before it occurred.

A sixth point is that when lives and fortunes are at stake, one should always consider the worst possible or worst likely outcome, rather than just seeing the world through rose-colored glasses. If things go well, no harm done. If things go badly, lots of harm done. So, if there are four indicators of a successful outcome but one of failure, one should take pains to avoid the failure if possible. At the same time, it seems that humans take notice of and can obsess about bad things more easily than good things, so one must be careful to not overreact to predictions of bad outcomes while not wishing them away either. In this case, even if some models at sometimes predicted a sooner collapse of Afghanistan, while others did not, the wise leader would have given due respect to the more disastrous predictions rather than just hoping they would not occur.

A seventh teaching point is that statistical tests depend upon assumptions about the nature of the variables being used or assessed or compared. Generally, it is assumed that data are random. Parametric statistics further assume the use of interval or ratio measurement of key variables (especially dependent variables) and of data being normally distributed. Nonparametric statistics do not need to assume the latter two points. If you use statistics where assumptions are not met, you may produce errant results. This is especially of concern if you are using complex multivariate statistics that require parametric assumptions but such assumptions are not valid. In our example, the results differed depending on the extent to which the assumptions were valid for the statistics used.

An eighth teaching point with respect to this report is that many statistics reviewed in basic statistics classes and texts [19] became part of this analysis – means, standard deviations, out-ofcontrol signals or control charts, graphing or visualization of data, paired samples t-tests, independent samples t-tests, statistical assumptions, nonparametric statistics, correlations and regression, and nonlinear regression.

A final teaching point is that even if data are found and are valid, statistical analyses can be performed incorrectly. Between invalid data and incorrect analyses, scholars are left to question the results of published research. For small data sets, N < 200, there are several ways to detect such problems and ultimately correct the scientific record [22]. Even if one cannot afford to purchase expensive statistical packages, many useful statistics can be obtained and used for free on the internet [23]. In addition to these teaching points, collaboration between statistics teachers and their students can occur in a variety of other areas, including as examples, articles that have investigated the importance of variance [24], evaluation of published articles that feature significant statistical errors [25], attempts to estimate standard deviations from the range [26-28], dealing with controversial or often misunderstood areas in statistics [29], reanalyses of published journal articles, which may reveal formerly hidden flaws [30], and statistical issues and problems associated with particular sub-disciplines (e.g., military families) of the social sciences [31].

Discussion

Even quadratic modeling could not capture the high rate of loss of provinces to the Taliban, which highlights the importance of catastrophe theory and the risk of relying solely upon statistical modeling (at least in two dimensions). Linear modeling would have predicted the fall of Afghanistan between November and December 2021 compared to between August and October for the quadratic modeling. While our comparisons between the predictions for the two models were not always significant statistically using only parametric statistics, the effect sizes ranged between 0.63 (medium or larger) and 2.94 (very large). Given that a late prediction of the fall might have more painful consequences, especially for public health, than an earlier prediction, an argument can be paid that more attention should have been paid to the earlier predictions from nonlinear modeling. Catastrophe theory may depend on critical changes in predictor variables; we would suggest that the United States decision to abandon Bagram Air Base and along with it, a variety of military support for Afghan military forces, may have been such a critical event. There may have been another critical event or events at the beginning of August 2021 (e.g., government soldiers collected their monthly pay and then went home?) just before the collapse accelerated even faster than earlier, but we are not going to speculate further on those possible events at this time. When President Biden stated on July 8th, 2021 that the fall of Afghanistan was not imminent, his advisors were probably basing that estimate on linear modeling and might have better advised him had they used nonlinear modeling and taken the principles of catastrophe theory in account in their development of their estimates. Perhaps a similar failure to consider nonlinearing modeling and catastrophe theory was behind senior officials from the Pentagon later testifying to the U.S. Congress that the rapidity of the fall of Afghanistan had taken them by surprise.

However, ordinary citizens with basic statistical training and an awareness of a variety of scientific theories, may, on occasion, be able to detect and recognize data patterns that may have been missed by national intelligence services across the globe; if we are wrong about this, perhaps those intelligence services would be willing to come forth and refute our results and prove that there was absolutely no way that Afghanistan could have been predicted to fall until perhaps some time in very late 2021 or early 2022. Alternatively, they might report that they did due diligence on predicting the fall of Afghanistan, perhaps better than we have done, but that their national leaders ignored their recommendations and advice. We feel compelled to note that our results also contradict, to some extent, the idea that “the Afghan army was routed in a week” [22, p. 1]. Yes, the loss of districts fell off a cliff in August 2021 but the losses had begun months earlier. A key turning point may have been around July 10th. While we have focused on catastrophe theory, others have noted that “Nonlinearities, positive feedbacks, abrupt collapses and regime shifts are being observed globally” [32] as cited by Peters [22], which might raise further questions as to how some political and military leaders seem to have failed to predict the collapse of Afghanistan.

Conclusion

From a public health perspective, the earlier than expected fall of Afghanistan may have led to a destruction of much of the public health infrastructure and personnel that had been built up over the previous twenty years. Those more educated in providing health care may have been more likely to depart Taliban control when they had a chance. If western style health care facilities are seen as “too western” or “non-Islamic” by some in the Taliban, such facilities might be damaged or destroyed. To what extent that such losses might have been mitigated or reduced by more accurate prediction of the timing of the Taliban takeover we may never know. However, there are some indications that food insecurity may be the preeminent concern over the winter of 2021-2022 [13], with other public health problems ensuing. Further research in this area might look to past regime changes to determine if nonlinear models or catastrophe theory would have applied to earlier situations. Should future situations occur that portended the decline of a government, nonlinear models might be tried then. While we tested mainly quadratic models, other models might work better in other situations. One candidate might be an exponential model. A step function model might also be useful if changes occurred with a series of declines followed by plateaus.

Other scholars may be able to develop a variety of other useful models or statistical methods more suited to past or future situations. Quality control models may also help to detect key turning points in the rise/fall of competing factions prior to a government’s collapse. It may be possible to use similar statistical methods to predict if and when military incursions into contested areas (e.g., Taiwan, Ukraine) might occur in the future, although that would depend on being able to select indicators that could not be easily disguised or obscured.

Funding

The preparation of this report received no funding from external sources or from either Kansas State University or Highland Community College.

Data Availability

See Table 1 above

Conflict of Interest

None reported.

Informed Consent Statement

Not Applicable (no human subjects).

Author Contributions

Conceptualization, WS; Methodology, WS, CAB; Formal Analysis, WS; Writing Original Draft, WS; Writing Review and Editing, all authors; Visualization.

Acknowledgement

None.

References

• Schumm WR, Webb FJ, Castelo CC, AkagiCG, Jensen EJ et al. (2002) Enhancing learning in statistics classes through the use of concrete historical examples. Teaching Sociology 30(3): 361-375.
• Lee Y, Schumm W R, Lockett L, Newsom KC, Behan K (2016) Teaching statistics with current and historical events: An analysis of survivor data from the sinking the HMT Birkenhead, the RMS Titanic, and the Korean ferry MV Sewol. Comprehensive Psychology 5: 1-6.
• Schumm W R, Crawford DW, Barkey P, EBush D, Bosch DW (2021) Using statistics to analyze anthropological/religious issues from the distant past. Insights of Anthropology 5(1): 337-346.
• Schumm WR (2020) How accurately could early (622-900 C.E.) Muslims determine the direction of prayers (qibla)? Religions 11(3): 1-15. 
• Schumm WR, Goldstein Z (2021) A statistical assessment of early Islamic history and the qibla: Comparing the theories of David King and Dan Gibson. Open Access J Archaeol and Anthropol 3(1): 1-20.
• Dean PJ (2021) Why the tragic Afghanistan withdrawal should reassure US allies in Asia. New Atlanticist 2021. Atlantic Council.
• Mott C (2020) Scenarios for post-U.S.Afghanistan. Defense Priorities.
• Johais E, Bayer M, Lambach D (2020) How do states collapse? Towards a model of causal mechanisms. Global Change Peace Security 32(2): 179-197.
• Sullivan CJ (2021) White flags: On the return of the Afghan Taliban and the fate of Afghanistan. Asian Affairs 52(2):  273-287.
• Rubin BR (2020) Afghanistan abandoned? Why an ailing American must not walk away. Horizons: J Int Relations and Sustainable Development 15: 136-143.
• BrittenS, Amer M (2021) Preventing collapse of the Afghan health service. Lancet 398(10310):1481.
• Safi N, Singh LS, Naseri S, AnwariP (2021) An alternative model for health service delivery in Afghanistan. Lancet 398(10310): 1481-1482.
• Wicks KS (2021) Where is Kareem? The story of Afghan souls.  National Catholic Register 97(26): 9-10.
• Gallagher M (2021) Leaving Afghanistan behind.  Esquire 176(2): 106-115.
• Stamovlasis D (2006) The nonlinear dynamical hypothesis in science education problem solving: A catastrophe theory approach. Nonlinear Dynamics Psychol Sci 10(1): 37-70.
• Alexander R A, Herbert GR, DeShon RP, Hanges PJ (1992) An examination of least-squares regression modeling of catastrophe theory.  Psychological Bulletin 111(2): 366-374.
• Roggio B (2021) Mapping the advances of the Taliban in Afghanistan.
• Aldrich JO (2018) Using IBM SPSS statistics: an integrative hands-on approach. 
• Brase CH, Brase CP (2015) Understandable statistics: concepts and methods 11^th (edn.).
• Cohen J (1992) A power primer. Psychol Bull 112(1): 155-159.
• Peters MA (2021) Declinism and discourses of decline the end of the war in Afghanistan and the limits of American power. Edu Philos Theory online advance.
• Schumm WR, Crawford DW, Lockett L, AlRashed A, Ateeq AB (2021) Nine ways to detect possible scientific misconduct in research with small (N < 200) samples. Psychology Research and Applications 3(2): 29-40.
• Schumm WR, Dugan M, Nauman W, Sack B, Maldonado J, et al. (2021) Using free websites to perform statistical calculations in basic statistics courses at high school or college levels.  SunKrist Sociology and Research Journal 2(1): 1009: 1-7.   
• Schumm WR, Bosch KR, Doolittle A (2009) Explaining the importance of statistical variance for undergraduate students. Psychol Edu An Inter Disciplinary J 46(3): 1-7.
• Schumm WR, Crawford DW, Fawver MM, Gray NK, Neiss ZM, et al. (2019) Statistical errors in major journals: two case studies used in a basic statistics class to assess understanding of applied statistics. Psychol Edu An Inter Disciplinary J 56(1): 35-42.
• Schumm WR, Higgins M, Lockett L, Huang S, Abdullah N, et al. (2017) Does dividing the range by four provide an accurate estimate of a standard deviation in family social science research? A teaching editorial.  Marriage & Family Review 53(1): 1-23.
• Schumm WR, Crawford DW, Higgins M, Lockett L, AlRashed A, et al. (2018) Estimating the standard deviation from the range: a replication of analyses of demographic data reported in Marriage & Family Review 2016-2017. Marriage Family Review 54: 777-792.
• Schumm WR, Pratt KK, Hartenstein JL, Jenkins BA (2013) Johnson GA Determining statistical significance (alpha) and reporting statistical trends: Controversies, issues and facts. Comprehensive Psychol 10: 1-7.
• Schumm WR, Brenneman RL, Arieli B, MayoTheus S, Muhammad J (2004) A statistica reanalysis of Brachman et al. (1962) study of a human anthrax vaccine. Medical Veritas 1: 171-178.
• Schumm WR, Crawford DW, Crow J, Ricklefs TK (2019) Clark KK Military family research: methodological lessons learned, often the hard way, updated with a eulogy for Dr. Bruce Bell.  Archives of Psychology 3(2): 1-22.
• Palinkas M (2018) Characteristics of collapsing ecosystems and the main factors of collapse. IntechOpen.