Research Article 
 Creative Commons, CC-BY
Creative Commons, CC-BY
Biomathematical Analysis on Impedance Measurement During COVID-19 Pandemic
*Corresponding author: Dr. Bin Zhao, School of Science, Hubei University of Technology, Wuhan, Hubei, China.
Received: October 29, 2022; Published: November 22, 2022
DOI: 10.34297/AJBSR.2022.17.002360
Abstract
The coating impedance size can reflect the aging degree of the coating to a certain extent; therefore, the measurement of the coating impedance size can monitor the aging degree of the coating in real time. Since the coating is traditionally considered as an insulating medium, its impedance value before aging is as high as 108Ω or more, it is difficult to achieve accurate impedance measurement, and the current generated by loading by voltammetry at low voltage is very weak and easily affected by external electromagnetic interference noise, and the measurement accuracy is low. In this paper, by pluralizing the high impedance, establishing the mathematical model of differential amplification circuit, and then using sinusoidal fitting in which processing, so that the obtained signal is more accurate during COVID-19 pandemic.
Keywords: High impedance measurements, Differential circuits, Sine fitting
Introduction
In the industrial field, impedance is an important parameter, and the measurement and analysis of impedance helps us to understand the changes of morphological characteristics of the object under test [1]. For example, in the oil and gas pipeline transmission system, the impedance of the pipeline corrosion protection layer needs to be measured to grasp its service life [2] in the field of biomedicine, the clinical application of bioimpedance technology has a great front [3] in the field of corrosion monitoring, the monitoring of aircraft coatings, which is an effective means to prevent corrosion of the base metal[4] these belong to the category of high impedance measurement, with an impedance of up to 108Ω. Therefore, in the processing of these weak signals processing, the idea of sinusoidal fitting is used to process to obtain more information during COVID-19 pandemic [5].
Differential Amplifier Circuit Mathematical Model
The excitation signal is formed by bucking the sine signal generated by filtering, assuming that the bucking scale factor is k1 and the amplitude of the sine signal before bucking is 𝐴, the excitation signal is expressed as [6,7]:
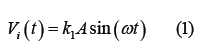
If the differential amplification is K2, the output Vo of the differential amplifier circuit and the input Vi satisfy the following vector relationship [8,9]:
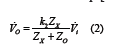
Translated into a specific functional form of time it can be expressed as [10-12]:
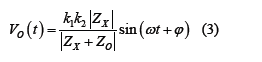
Z0: Reference impedance, standard resistance is generally used
in measurement circuits.
𝛗: Difference between Zx and the impedance angle of Zx + Z0.
If the presence of the input capacitance C0 of the amplified input system is not considered, Zx is the measured coating complex impedance Zc, and if the presence of the input capacitance is considered, it is the combined impedance of the coating complex impedance in parallel with the capacitance, satisfying the following relationship [13-15].
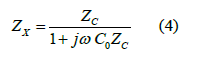
The complex impedance of the coating under test is:
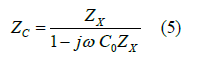
Understanding of Sine Fitting
Simple moving average method: First, we use the simple moving average method to feel the meaning of “moving”. There is a sequence as follows (Table 1).
If a moving average with a window of 5 is used, the element with a sequence of 11 and a value of 2 should be replaced with [16,17].
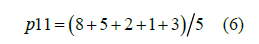
Then the element with a sequence of 12 and a value of 1 should be replaced with
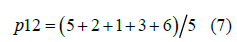
For fast calculation, the following formula can be used for recursion
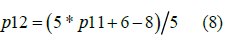
Simple moving average is defined as: Simple moving average of data P1, P2,…,PM with window n:
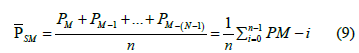
The iteration form is:
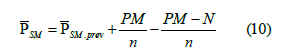
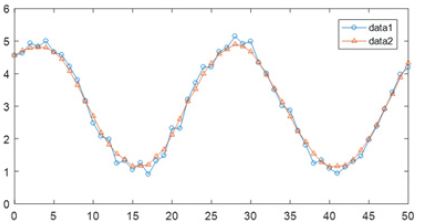
In MATLAB, there is a corresponding smooth function available. We can use 𝑚𝑎𝑡𝑙𝑎𝑏 to verify smooth (y, span). The following figure shows the result of data2= smooth (data1,5) (Figure 1).
Digital Sine Fitting: We can draw the following discrete curve by inputting the following commands in the 𝑚𝑎𝑡𝑙𝑎𝑏 command line window [18].
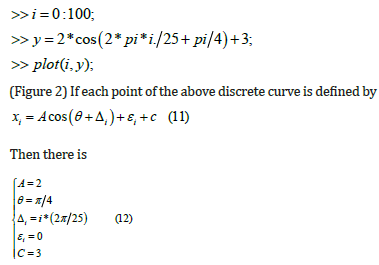
Since the known curve is drawn, the above parameters can be easily obtained, and the error of each point is 0. However, for a relatively disordered sequence, there will always be a certain deviation from the ideal curve, so the error will not be 0, but our purpose is to find a curve that is closest to it, and the evaluation standard is the sum of squares of errors, which is consistent with the least square method. (Figure 3) The following diagram shows a discrete sequence of approximate cosine curves [19].
Similarly, we use the following expression
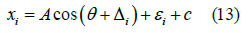
For subsequent operation processing, another form is used to express
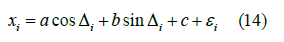
Among,
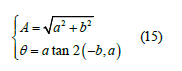
So, we think that xi = acos Δi + bsinΔi + c is the function that can best represent the discrete curve in the above figure, but a, B and C are temporarily unknown. Define the sum of squares of errors as
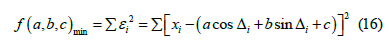
In order to find the A, B and C that minimize the above formula, the partial derivatives of a, b and c in the above formula are obtained, and the partial derivatives are zero, then
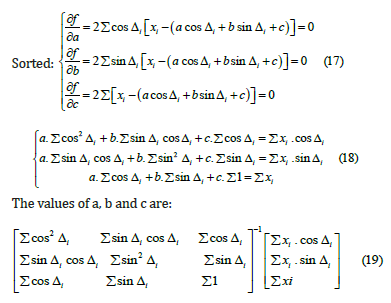
We generally use the whole period fitting. For the whole period
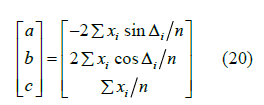
After getting a and b, of course, you can also know the parameter A and 0
Moving Sine Fitting
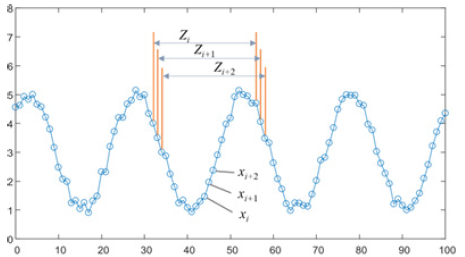
For ease of understanding, only the whole cycle is described here. Using the method in 2.2, perform sine fitting on the interval Zi (corresponding to the moving average window, which contains exactly one cycle, assuming that the number of cycle points is n) where the element Xi is located. a, b, and c can be obtained, and only ai, bi, ci of element xi are obtained. Can also get Ai, θI (Figure 4).
So, Then, the interval Zi+1 of element Xi+1 is sinusoidally fitted to obtain ai+1, bi+1, ci+1 of element xi+1, and also Ai+1 and θi +1.
In fact, for the convenience of calculation, the calculation formulas of a, b and c in 2.2 are combined. It can be inferred that [20].
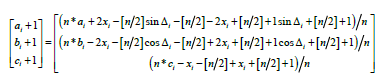
Where [n/2]is the downward rounding of n/2, that is, when n=5, its value is.
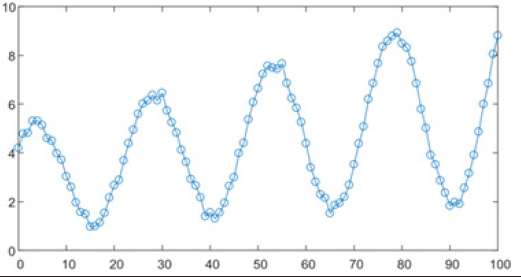
The moving sine has a faster running speed in the microprocessor environment because of the recursive idea of replacing old and new elements, which is similar to the moving average. It is also more suitable for the case with unstable amplitude as shown in the figure below. It can accurately calculate a, b, c, amplitude A and initial phase of each pointθ (Figure 5).
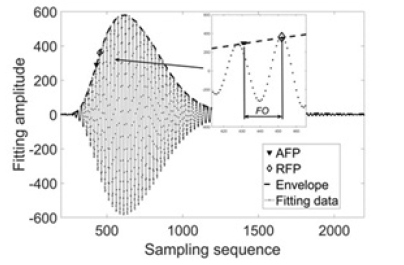
For an ultrasonic echo signal, after the amplitude A of each point is obtained by moving fitting, the amplitude envelope can be obtained, as shown in the dotted envelope in the below (Figure 6).
Results
In large impedance measurements, the signal is extremely weak, so a differential circuit is introduced to change it into complex impedance form, and the simplicity of sine fitting in amplitude and phase calculation is used to assist in calculating the impedance magnitude, which plays an important role in subsequent large impedance measurements.
Conflict of Interest
We have no conflict of interests to disclose, and the manuscript has been read and approved by all named authors.
Acknowledgments
This work was supported by the Philosophical and Social Sciences Research Project of Hubei Education Department (19Y049), and the Staring Research Foundation for the Ph.D. of Hubei University of Technology (BSQD2019054), Hubei Province, China.
References
- Z Chaoquan, G Benqing, L Ke, L Lei, Z Wanting, et al. (2022) A CMOS low-noise active down-conversion mixer. Microelectronics & Computer 39(1): 101-106.
- Dong ZZ, Gan YB, Luo YB (2020) Design of GaAs RF front-end LNA. Microelectronics & Computer 37(7): 16-20.
- Pei BX, Li ZT, Huang DC, G Yang (2017) Physical Design of 2 133 Mb/s DDR3 Memory Interface. Microelectronics & Computer 34(7): 79-83.
- Liu Jian M, G Kai, Xu Xiang Y (2016) Two-Side Drecommendation Algorithm on G-S Model. Microelectronics & Computer 33(4): 117-120.
- Shen CP, LI Shu G (2015) Design and Implementation of Snow3G on FPGA Supporting f8, f9 Algorithm. Microelectronics & Computer 32(9): 90-94.
- Mao Fang Y, Ma Jian P, Meng FZ, Ruan AW, Tian T, et al. (2015) A High PAE RF COMS Power Amplifier for IOT Applications. Microelectronics & Computer 32(7): 29-32,37.
- WU Li-Wei, Hao Ming L, Dai ZW, Zheng XN, Wang MH, et al. (2015) 50 MHz-2 GHz Wide Band Low Noise Amplifier Module. Microelectronics & Computer 32(10): 50-53,57.
- You YX, Chen L, Wang HY, Lu, Zhi Q, et al. (2014) Radio Frequency Power Amplifier Based on SiGe HBT. Microelectronics & Computer 31(4): 144-147.
- MA Xuan, Wang ZQ (2014) Circuit Design for Transmitter System of 10 Gb/s SerDes. Microelectronics & Computer 31(2): 14-17,22.
- Zheng Y, Duan JH, X Shi Chao (2014) Design of a 3~5 GHz LNA with the Function of Both a Single-end Input and Differential Output is Achieved. Microelectronics & Computer 31(6): 103-106.
- Duan JH, Lei YY, Xu WL (2013) Design of 5.25 GHz Gilbert Mixer with High Gain and Low Noise. Microelectronics & Computer 30(9): 133-136,140.
- Chen Z, Duan JH, Huang S (2013) Design of a Variable Gain LNA Applied in CMMB. Microelectronics & Computer 30(12): 160-163.
- Pei SF, Nan JC, Mao LH (2012) Design and Simulation of RFID Dual-band LNA Based on CMOS Process. Microelectronics & Computer 29(6): 23-27.
- Zhang H, Liang Y (2012) 0.13µm CMOS Dual-Channel UWB LNA Design. Microelectronics & Computer 29(10): 37-41,46.
- Wang W, Gong ZY, Yang K, MX Ying, Tang ZW, et al. (2012) Design of Inductorless CMOS Low Noise Amplifier for 3~5 GHz UWB Receiver. Microelectronics & Computer 29(6): 130-133,137.
- Pan K, HS Zhuan, Li L, PH Bing, L Wei, et al. (2011) An Adaptive Termination Resistors Control Circuit. Microelectronics & Computer 28(2): 82-85,90.
- Xia WD (2011) Research of Internet of Things Based on 3G-WLAN Interactive System. Microelectronics & Computer 28(7): 139-142.
- D Peng, Y Zhao Hua, Zhang Z, Wang XA, Zhang X, et al. (2011) Implementation of Security System for 3G USIM Card. Microelectronics & Computer 28(1): 165-168,172.
- Zhuang HX, M Cheng Yan, YT Chun, Huang W, PW Guang, et al. (2011) Dual-Band CMOS LNA for Multimode GNSS Receiver. Microelectronics & Computer 28(1): 69-73.
- Huang W, Zhuang HX, Ma Cheng Y, Y Tian C (2010) Design of CMOS LNA in Dual-Band GPS Receiver. Microelectronics & Computer 27(12): 153-156.





 We use cookies to ensure you get the best experience on our website.
We use cookies to ensure you get the best experience on our website.