Research Article 
 Creative Commons, CC-BY
Creative Commons, CC-BY
Nasal Valve Manometry by Differential Pressure Measurements
*Corresponding author:M Gamerra, ENT Department ASL NA3 Sud, 80053 Castellammare di Stabia (NA), Italy
Received:February 7, 2023;Published:March 06, 2023
DOI: 10.34297/AJBSR.2023.18.002439
Abstract
The effects on air flow of a septum spur, located in the nasal valve, are studied both theoretically and experimentally. The analytic investigation on the differential pressure between two points in the nasal valve has been carried out by means of the Bernoulli’s equation in the limit of stationary, non- dissipative and laminar air flow. On the experimental side, the nose and sinus manometer has been adapted with a double-ended probe to make differential manometry measurements. It can be argued that the differential pressure approach is useful to investigate the fluid dynamical anomalies induced by a nasal septum spur.
Introduction
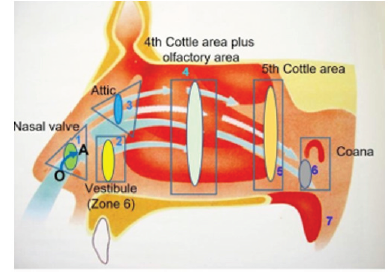
Differential pressure refers to the difference in air pressure from one location to another within a system. Differential pressure between two points in the nose is related to a correct ventilation of the inner cavities by which infections and contaminations can be prevented [1]. The nasal area [2] is a three-dimensional region, that is, a volume delimited by well-defined borders, which can be altered by anatomical anomalies [3]. The rhinologist surgeon aims at modifying and normalizing, in shape and size, the inner nasal contour. Cottle [4] divides the interior of the nasal pyramid into 5 areas: vestibular, valve, attic, anterior and posterior parts of the turbinates and of the choanal opening. Deformations of the Cottle areas and of the related fluid-dynamical resistances can severely affect the respiratory dynamics [5]. In the present work, we analyse the fluid-dynamical effects of deformations in the nasal valve (Figure 1).
Differential Pressure Concepts
When describing air flow from point O in the nasal valve to point A in the nose cavity (see Figure 1) it should be noted that the pressure gradient pA − po is negative, due to the depression generated by lungs. In this case we can talk about gauge pressure since point O is at atmospheric pressure. If air flow is considered laminar, non-viscous and irrotational, but not stationary, Bernoulli’s theorem for non-stationary fluid flow may be applied. In fact, under these conditions and in the limit of low velocities, air can be considered an ideal fluid. The main effect of this pressure gradient is a difference in the velocities, 𝑉𝑂 and 𝑉𝐴, of the fluid in points O and A, respectively. In fact, by writing Bernoulli’s equation for nonstationary fluid flow, we have:

where 𝑎𝑥 is the acceleration (assumed to be uniform over the path along the 𝑥-direction (going from O to A) of the fluid and x = xA − xO Is the (positive) distance between points O and A. When inertial effects are neglected and the velocity 𝑉O is taken equal to zero, Formula 1 reduces to the following:

So that a constant velocity can be maintained at steady state at point A of the nasal valve (see figure 2). Let us now consider the same sector with two different sections of cross-sectional areas 𝑆𝐴 in 𝐴 and 𝑆𝐵 in B, as in Figure 2. We can thus rewrite Equation (2) also for point B as follows:
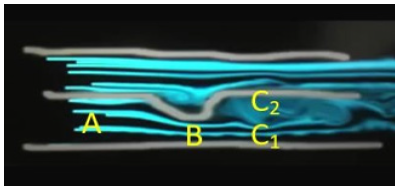
Figure 2:Two adjacent regions, A and C, separated by a nasal spur in B. Region C consists of two subregions, C1 and C2, with different fluiddynamical properties

(Figure 2) The differential pressure ΔpAB = ρB − p now be defined, according to Equation (2) and (3), as follows:

In the case shown in Figure 2, however, 𝑉𝐵 is greater than 𝑉𝐴. In fact, point B can be considered a nasal deviation reducing the cross section in that sector, so that 𝑆𝐴 > 𝑆𝐵. In fact, by mass conservation

so that


Therefore, the highest is the ratio SA/SB the most negative is the differential pressure Δ𝑝. This differential pressure can be measured by means of the nose and sinus manometry using a two- terminal probe (see Figure 3), fit for getting the values of the pressure in points 𝐴 and 𝐵 [5]. Beyond point B, the cross section of the same sector is equal to 𝑆𝐴, but with different flow pattern. In fact, the considered nasal valve anomaly affects air flow properties in points 𝐶1 and 𝐶2, as shown in Figure 2. Let us then assume that the region beyond point B is formed by two subregions of cross- sectional areas Sc1 and 𝑆𝐶2, respectively. In this way, by proceeding as in Equation (6), for 𝐶1 we may set:

Being the flow pattern in 𝐶1 very similar to that in B, we expect a very small value of. On the other hand, assuming that we can still apply Bernoulli’s equation in the region close to point 𝐶2, we may write:

having set the velocity 𝑉𝐶2 close to point 𝐶2 equal to zero. Therefore, we can summarize these results by saying that the differential pressure between points 𝐶1 and B is approximately equal to zero, while the differential pressure between points 𝐶2 and 𝐵 is positive. In terms of fluid flow patterns, we may therefore say that air flow velocity in 𝐶1 is almost equal to 𝑉𝐵, while a stagnation region is formed around point 𝐶2.
Methods
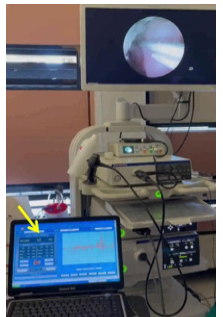
The work was performed in accordance with the principles of the 1983 Declaration of Helsinki. The study was approved by the local board of medical ethics. Written informed consent was obtained from all participants prior to the inclusion in the study. Twenty non-smoker Caucasian subjects suffering from incomplete nasal valve sub-obstruction were enrolled [6,7]. All of them underwent nasal endoscopy. The sample was homogeneous by age, sex, and body weight (10 M, 10 F; mean age 42.64 ±13.1) (Figure 4). To carry out pressure measurements, we used the DDM-MG1 patented manometer. Technical characteristics of this digital manometer can be obtained in reference. [8,9]. The differential pressure has been measured by means of the nose and sinus manometry using a two-terminals probe (double-ended), spaced apart by 0.5cm, fit for getting the values at the same time in two close points of the nasal valve deviation, for points A-B, B-C1, B-C2 (See Figure 2). The probe was placed in these points under endoscopic guidance. Subjects were asked to breathe through the nose for four seconds slowly and deeply [9-10] while the selected nasal area was checked by video-endoscopy for the entire duration of the examination (see Figure 4). This respiration pattern is adopted to avoid turbulent flow. The manometer was connected to a computer with software for visualization and recording of pressure values. Data supporting this study is included within the article.
Results
In Table 1 we report the average peak values of the differential pressure, expressed in mbar. Experimental data for sectors A-B, B-C1, B- C2 were gathered for both groups of patients. We obtained an average peak of the differential pressure of -0,3 mbar for sector A-B, of about 0,0 mbar for sector B-C1 and of +0,1 mbar for sector B-C2 (Table 1).
Discussion and Conclusions
Considering the experimental values for the differential pressure between points A and B (second column in Table 1), we notice that they are negative, as predicted by Equation (6). The small values of the pressure gradient allow stationary air flow without generating turbulences. As for the experimental values for the differential pressure between points B and C1 (third column in Table 1), we notice that they are almost equal to zero since the velocity profile does not vary appreciably. Finally, for the experimental values for the differential pressure between points B and C2 (fourth column in Table 1), we notice that they are positive, as predicted by Equation (8), since higher pressure in the stagnation region C2 is present. The differential pressure approach is thus useful to investigate the fluid dynamical phenomena induced by the presence of a nasal valve deviation. In this respect, we notice that the reduced size of the probe allows a pinpoint measurement localized with precision in the chosen valve area, not modifying the anatomy or the air flow pattern during measurements. In this respect, we also mention that the nose-sinus manometry allows us to detect the pressure values at the “critical points” under investigation in real time. Finally, we may notice that this method can be adopted for any point of the nasal cavity where a septum spur is present. All authors declare that they have no conflicts of interest. This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Conflict of Interest
No conflict of interest.
Acknowledgement
None.
References
- Montes Bracchini JJ (2021) Preservation Rhinoplasty (Let-Down Technique) for Endonasal Dorsal Reduction. Facial Plast Surg Clin North Am 29(1): 59-66.
- Saban Y, Daniel RK, Polselli R, Trapasso M, Palhazi P, et al. (2018) Dorsal Preservation: The Push Down Technique Reassessed. Aesthet Surg J 38(2): 117-131.
- Kern EB (2021) History of Dorsal Preservation Surgery: Seeking Our Historical Godfather(s) for the "Push Down" and "Let Down" Operations. Facial Plast Surg Clin North Am 29(1): 1-14.
- Patel PN, Abdelwahab M, Most SP (2021) Combined Functional and Preservation Rhinoplasty. Facial Plast Surg Clin North Am 29(1): 113-121.
- De Luca R, Gamerra M, Sorrentino G, Elena Cantone (2014) Nose and Sinus Air Flow Model. Natural Science 6: 685-690.
- Huizing EH, De Groot Johan AM (2003) Functional Reconstructive Nasal Surgery. Stuttgard Thieme.
- Yu S, Liu Y, Sun X, Shouju Li (2008) Influence of nasal structure on the distribution of airflow in nasal cavity. Rhinology 46: 137-143.
- Gamerra M, De Luca R, Pagano G, M Merone, M Cassano, et al. (2013) The nose and sinus manometry: a bio-physical model applied to functional endoscopic sinus surgery. J Biol Regul Homeost Agents 27:1021-1027.
- Gamerra M, De Luca R, Cantone E, M B Russo, E De Corso, et al. (2017) Mathematical model for preoperative identification of obstructed nasal subsities, Acta Otorhinolaryngoiatrica Italica Epub 37(5): 410-415.
- Gamerra M, Bruno R, Pagano G, et al. (2004) The nose function and aesthetic. Ann Otorhinolaringology Iber-Amer 31: 307-323.





 We use cookies to ensure you get the best experience on our website.
We use cookies to ensure you get the best experience on our website.