Research Article 
 Creative Commons, CC-BY
Creative Commons, CC-BY
The Application of Hybrid Methods to Solve Some Problems of Mathematical Biology
*Corresponding author:VR Ibrahimov, Institute of Control System named after Academician A Huseynov, Computational mathematics, Baku State University, Baku, Azerbaijan.
Received:February 13, 2023 Published:February 24, 2023
DOI: 10.34297/AJBSR.2023.18.002436
Abstract
Recently, the number of papers devoted to the application of mathematical methods to solving biological problems has increased. Scientists have constructed new methods that have novel properties. As is known, a mathematical model of the problem of biology is constructed by biologists, and the solution of such models is investigated mainly by mathematicians using some mathematical constructs. As such an example, consider the problem of animal population. Given that mathematical biology emerged at the intersection of biology and mathematics, here to solve some problems of mathematical biology are invited to apply methods that are constructed at the intersection of one step and multistep methods which are called as hybrid methods. For solving these problems here are proposed stable hybrid methods with the higher order of accuracy. Here are constructed concrete stable hybrid methods with the order of accuracy and methods constructed by using linear part of the function located in the right-hand side of the differential equation, some of which are illustrated in the specific examples. It is also shown that for the stability of ecosystem, the law its conservation must obey the exponential law. To calculate the reliable values of the solution of the problem under study at the mesh points, here suggested. For this aim have constructed simple bilateral methods for solving some mathematical biological models.
Keywords: Mathematical biology, Stability of ecosystem, Hybrid method, Linear and nonlinear mathematical models
Introduction
Man with the appearance on earth began to study the environment. To this end, he studied populations of organisms of different species. Among them are the simple communities of organisms of one species. Naturally, the model describing such isolated population is simplified and consists essentially of a population, and the intersection between the resources. If we denote by n(t )- population size, and through r (t ) - the amount of resources at the moment t, then the change of the resource based on the law of conservation of mass can be written as:

Here is denoted through r (t ) the derivative of the function r (t ) at the time t, Q-arrival rate of resources in a “resourceconsumer” (population), but through V (r,n)- rate of resource consumption by one individual populations. “In the study of population,one of the main” questions is to determine the number of organisms at the given time t, which can be solved by the help of the following ordinary differential equation of the first order :

Here m is the coefficient of the mortality rate. It is known that the study of ecosystem represents both theoretical and practical interest. Research in this system shows that the stability of the ecosystem is dependent on its complexity. If the system is complex, it is more stabilized. For example, a system consisting of two conflicting populations, which can be taking as the “predator-prey”, which investigated by some scientists and generally unstable. Note that, for the study of ecosystems is taken a look to the investigation of the finding number of organisms at age τ at the time t. If we denote by x (τ ,t )- the number of individuals at age τ at the time t, then its rate of change is determined by the following equation:

Here, the function K ( X ,t,τ ) is called coefficient of the mortality rate, which depends on the coefficient of natural mortality m and competition within the species:

The equation of the birth rate can be written as:

Noted that the model Stokes, Darcy and Brinkman, which has investigated in [1], similarly to the model (3).
Given the results of numerous studies in the field of population, scientists argue that population development is described using exponential functions, which are usually stable. This is confirmed with the help of some mathematical models which have the following form:

Reddits: Topics on the social networking site reddits contain content and comments on some topics(submissions) about abortion and gun control (Figure 1.1-Figure 1.2b).
As is known the biological potential, also is expressed through exponential functions. Let remark that mathematical biology as scientific direction, emerged at the intersection of two sciences. Many scholars have considered scientific field of mathematical biology as a separate science. It is known that in the field of mathematical biology mainly are studied mathematical models of biological problems. One of these problems is mathematical model of classical problem of the “predator and prey”. [1-5]:

Here α, β, γ and δ-are some known quantities. It is obvious that the proposed model can be solved as a system of ordinary differential equations of the first order. However, the specified model can be reduced to a second-order differential equations, or to integral equations of Volterra type. In [6] to study the populations of some species, have constructed the mathematical model in the form of the integro-differential equations, but in [7], for this purpose have used the differential equations. If generalize the models described above, then obtain the following problem:

Suppose that problem (6) has a unique solution determined on the segment [X0, X].
On Some Simple Methods for Solving Problem (6)
For construction numerical methods let us divide the segment [x0,X] into N equal parts by the constant step-size h > 0 and determine the mesh points in the following form: xi=x0+ih, (i = 0,1,..., N) . Denote by yi “ the approximated values and by the (i=0,1,2...N ) exact values of the solution of problem (6) at the mesh point ( 0,1,2,....) The approximate values of the function f (x, yi) at the point (I-0,1,2...) will be given by the following description: fm=f(xm,ym),m=0,1,2,3...N.As is known, the popular methods of the problem (1) is the one step and multistep methods.
It is known that the Runge-Kutta method, which applied to solving of the problem (6), may be written as follows:

Let us consider the multistep method, which can be written as the following:

The known Adams-Moulton and Adams Bashfort can be received from the method of (8) as the partial case. In references, this method is called the k-step method with constant coefficients. It is shown that there are some relationships between methods Runge-Kutta and multistep (see for example [7,8]. As is known the basic conception for the compares of the methods of type (8) are the stability and degree, but for the method (7) are used conception of order or the degree. It is known that if the methods (8) are stable, p ≤ 2[k 2]+ 2 then [9]. Method (8) is called stable, if the roots of the polynomial


here k-is the order of the method (8). Equality (9) for the method (7), can be presented as follows:

here x = x0 + nh is fixed point.
For example,


As is known the implicit Euler method can be presented as following:

It is not difficult to prove that the following is holds:

From here it is received that methods (11) and (12) can be taken as the bilateral method. By this way one can find the reliable results. And let us note that this bilateral method is very simple. But in some times can be aris the necessity in solving nonlinear equation (12). For solving this equation one can be used the following way:

For the receiving more reliable results, here recommended to use the following advanced method:

This method has the degree of, but methods (11) and (12) have the degree. For the finding the values and participating in (13), one can used the method (11) and (12), or trapezoidal rool. To receiving more exact values of the solution of investigated problem one can be used the following:

This value will be more exact, namely

A Way to Construction More Exact Numerical Methods with the Constant Coefficients
In the middle of the XX century, the scientists constructed procedures which are called hybrid methods [10-16]. Hybrid method can be presented in the following form:

One of the first hybrid method of type (14) is the midpoint rool, which has the following form:

Hybrid method in single form can be written as following:

This method is more precise than the corresponding classic Runge-Kutta and Adams methods. If to generalize it, then in results of which receive the following:

Obviously, method (12) is the multistep hybrid methods with the constant coefficients. Note that the integer-value quantity p is called the degree of method (12) if the following asymptotic equality is holds:

Note that usually as the notation of the order of accuracy of the multistep hybrid methods are used the symbol of p methods [17]. One of the basic questions with evaluating this method is that of defining the relationship between its degree and order. Before establishing this relationship, let us consider some restrictions imposed on the coefficients of the method of (16).
A: The coefficients αi,βi,γi and li(i=0,1,2,...,k) are
some real numbers, moreover, αk≠0.
B: The characteristic polynomials

have no common multiple different from constant.

By the method of undetermined coefficients, we can examine the define of the quantities αi,βi,γi and li(i=0,1,2,...,k) so we will consider the following expansion:

where x = x0 + nh is a fixed point.
Note that the values of the coefficients of the multistep method in some sense relates to the relationship between the order and degree of method (16), therefore, we require the following lemma.
Lemma. Let y (x) be a sufficiently smooth function, and assume that conditions A, B, and C are holds. For method (16) to have the degree p, satisfies the following conditions its coefficients are necessary and sufficient:

Proof. We first prove that if method (16) has the degree p, then the coefficients αi,βi,γi and li(i=0,1,2,...,k) will satisfy the system of nonlinear algebraic equations given in (20). Considering that the method (16) has the degree p, then by using Teylor expression (18) and (19) in the left hand-side of asymptotic equality (17), we have:

From that the method (16) has the degree p, we obtain the following:

As is known that 1, x, x2 ,..., xp is a linearly independent system therefore, equality (22) is equivalent to the following:

We now will prove that if the coefficients of the method (16) is the solution of the nonlinear system (20), then its degree is equal to p. Indeed, if we used the system of equalities of (23) into equality (21), then we obtain the asymptotic equality of (17). It follows from this asymptotic equality that, method (16) has the degree of p. It is easy to determine that by the chosen values li=0(i=0,1,...,k ) , the system (23) will be linear and coincides with the known system used for defining the coefficients of the multistep method with constant coefficients presented as (8). Subject to the conditions from l0 + l1 +...+ lk ≠ 0 , system (23) is nonlinear. This system contains from the p+1 equations in 4k + 4 unknowns and is homogeneous, it must possess the zero solution, and for system (23) to have a non-zero solution, suppose that 4k + 4 > p +1is holds. Hence, we obtain that there are methods of type (16) with the order p ≤ 4k + 2 .
On Some Specific Methods with the Certain Accuracy
Consider the construction methods of type (11) and suppose that k=1. Then, under the assumption that α1=−α0 =1 and β1 = β0 = 0, from the system of (15) we will have the following system for the determined of variables γ0 ,γ1 ,l0 and l1 :

Here, l = 0 and γ2 =1 + l . Solving this nonlinear system of equations for l and γ in results receive the following quadratic equation: l2 − l +1 6 = 0 .The value of γ is determined from the equation γ + l =1. Note that the method with the degree p = 4 can be written as follows:

This method is an implicit hybrid method with degree p=3 and is A-stable [16-22].
Consider method (16) for k=1. In this case, assuming that α1 = −α0 =1, system (20) takes the following form:

The solution of this nonlinear system yields the following:

The corresponding method with degree p=6 takes the following form:

To apply hybrid methods to solving of some problems, we should know the values of


This method is explicit and has degree p=5. To use method (28) we must define



It is known that some authors to solve the problem (6) propose methods using derivatives of the function f (x, y) [27-35]. For example, the following method:

Noted that if method (29) is stable and has the degree p, then the following is holds: p ≤ 2k + 2 And if the method (16) stable and has degree of p, then p ≤ 3k + 3. Therefor the method (16) is more promising.
For the application of the methods (27) one can be used algorithm from many known models describing some processes of natural sciences, which have formulated in the form of linear differential equation. For this aim let us consider to investigation of fish population. We denote the number of fish through y(t) at time t. Then to find of y(t), one can be used the following model [36]:

In some cases, the values of the coefficients and functions can be assumed to be known. Then for solving of the above mentioned equation one can use different numerical methods. Obviously, after the generalization of these model, we have:

Such generalization allows us to investigate some different populations by one model. For example, the model describing the dynamics of closed populations for different individuals can be obtained from the model (31) at F(t, y) = a(t ) y +ϕ (t ) . It is clear, that a (t ) y is principal term. in the function F(t, y) . Consequently, in the investigation by the existence of ecosystem are determined properties of the principal term of the function F(t, y) .Thus we receive that if the existence of ecosystem to obeys an exponential law, then the ecosystem may be stable.
To solve such problems at a(t ) ≡ const, here offer the following scheme:

Numerical Results
To demonstrate the advantages of the methods, which have been motioned above, here consider their application to solving of the following problem, which is a form of problems such as Lotka- Volterra.

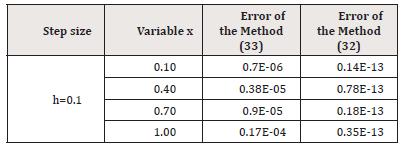
Results tabulated in table 1 for λ = −1 and in table 2 for λ =1.
Some authors are applied the Euler, Rozenbrok and the method (32) to solving the following problem [35,36]:

The results obtained by the method (32) turned out to be the best. The problem (34) is one of the fish populations [37-40]. As is known, the problem studied here has a world that is associated with some physical problems (see for example [37-40].
Remark
In section 1, have constructed bilateral method by usin Euler’s explicit and implicit methods. Application of this method to solve some specific problems one can use the following algorithm.
Algorithm 1

Algorithm 2

Conclusion
We have constructed a multistep hybrid method with the degree 4 ≤ p ≤ 6 for k=1. It is known that for k=1, the ordinary k-step method has maximal degree max p = 2 , which yields a trapezoidal method. However, the hybrid approach constructed here has maximal degree max p = 6, although the application of the trapezoidal method is simpler than applying a hybrid procedure. Using the Euler explicit method in place of the predictor method, one can construct a predictor-corrector scheme for the practical application of the trapezoidal method (see remark). Note, that for construction stable methods with the degree p = 2k + 2 , one can be used multistep methods with the second derivatives [13,19]. Here we have used a block method to construction of algorithms for using hybrid methods. Note that when using hybrid methods there are some difficulties with the calculated values of solutions of the original problem in hybrid points. However, if there is no need for finding approximate values of solutions of the problem with high accuracy, then can be use simpler methods for example method (26). It is clear from the above mentioned that the methods, which are used the linear part of the function f (x, y)on y are more promising than the others. Usually these methods are A- stable. Consequently, by the application of these methods to solving of some biological problems can achieve the desired result. Therefor we are recommended methods of type (32) to solve biological problems. At the end we remark that, if are known minimal information about biological problems, then we receive the linear model for solving, which the methods of type (32) are promising. Note, that if we are investigate of the stable ecosystem, for which are used the minimal resources for the existence with respect to the system consisting of two organisms, such as the system “predator - prey”, then we receive that changing of the resource functions k (t )must to obey the exponential law (R(t )) = exp(a (t )).Therefor we are recommend methods of type (32) to solving biological problems. So, if are known minimal information about biological problem, then we receive the linear model [20-40].
Acknowledgements
The authors wish to express they’re thanks to academician Ali Abbasov for his suggestion to investigate the computational aspects of our problem and for his frequent valuable suggestions. This work was supported by the Science Development Foundation of Azerbaijan (Grand EIF2011-1(3)-82/27/1). We are also grateful to the referees whose useful suggestions greatly improve the quality of this paper.
Conflict of Interest
None.
References
- Ortega JM, Poole WG (1986) An Introduction to Numerical Methods for Differential Equations. Pitman Publishing Inc (Russian).
- Hairer E, Lubich Ch, Wanner G (2006) Geometric Numerical Integration. Second Edition, Springer.
- Volterra V, D Ancona U (1935) Les Associations Biologiques au Point de Vue Mathematique, Hermann Paris.
- Enrite WH (1974) Second derivative multistep methods for stiff ordinary differential equations. SIAM J Numer Anal 2: 321-332.
- Mehdiyeva G, Imanova M, Ibrahimov V (2012) An application of the hybrid methods to the numerical solution of ordinary differential equations of second order. Kazakh ∨∨ National University named after Al Farabi Journal of treasury series mathematics mechanics computer science Almaty 75 (4): 46-54.
- Nakhushev AM (1995) Equations of Mathematical Biology, Moscow, Visshaya shkola (Russian).
- Skvortsov LM (2009) Explicit two-step Runge Kutta methods Math. modeling, 21(9): 54-65.
- Mehdiyeva GY, Nasirova II, Ibrahimov VR (2005) On some connections between Runge-Kutta and Adams methods Transactions issue mathematics and mechanics series of physical-technical and mathematical science 5: 55-62.
- Butcher JC (2008) Numerical methods for ordinary differential equations. 诣John Wiley and sons, Ltd: 463.
- Mehdiyeva GY, Imanova MN, Ibrahimov VR (2013) On one application of forward jumping methods. Applied Numerical Mathematics 72: 234-245.
- Butcher JC (1965) A modified multistep method for the numerical integration of ordinary differential equations J Assoc Comput Math 12: 124-135.
- Mehdiyeva GY, Imanova MN, Ibrahimov VR (2011) On one generalization of hybrid methods $ Proceedings of the 4th international conference on approximation methods and numerical modeling in environment and natural resources Saidia, Morocco may 23(26): 543-547.
- Gear CS (1965) Hybrid methods for initial value problems in ordinary differential equations SIAM. J Numer Anal 2: 69-86.
- XG Yue, Z Zhang, A Akbulut, Mohammed KA Kaabar, Melike Kaplan, et al. (2022) A new computational approach to the franctional order Liouville equation arising from mechancs of water waves and meteordigical forecasts. Journal of ocean enginering and science 15: 1-8.
- H Han, L Sicheng, H Lin, D Nelson, M Otilia, et al. (2019) Risk factor identification of stestomable guarantee network based on logictic: regression algorithm. Sustoinability 11(13): 1-9.
- GK Gupta (1979) A polynomial representation of hybrid methods for solving ordinary differential equations. Mathematics of comp 33(148): 1251-1256.
- M Imanova (2006) One the multistep method of numerical solution for Volterra integral equation, Transactions issue mathematics and mechanies series of physical -technical and mathematical science I: 95-104.
- Hammer PC, Hollingsworth JW (1955) Trapezoildal methods of approximating solution of differential equations. MTAC 9: 92-96.
- MK Kaabar, F Martinez, IF Gomez Aguilar, B Ghanbari, M Kaplan, et al. (2021) New approximate-analytical solutions for the nonlinear fractional Schrōdinger equation with second-order spetio-temporal dispersion via double laplace transform method. Matbematics 44(14): 11138-11156.
- Dahlquist G (1956) Convergence and stability in the numerical integration of ordinary differential equations. Math Scand 4: 33-53.
- Ibrahimov VR (1982) On a nonlinear method for numerical calculation of the Cauchy problem for ordinary differential equation Diff. equation and applications. Pron. of II International Conference Russe. Bulgarian 310-319.
- VR Ibrahimov, GY Mehdiyeva, Xiao Guang Y, MKA Kaabar, S Noeiaghdam, et al. (2021) Novel symmetric numerical methods for solving symmetric mathematical problems Novel 15: 1545-1557.
- G Mehdiyeva, M Imanova, V Ibrahimov (2016) British Journal of Applied Science & Technology 1-15.
- Makroglou A (1982) Hybrid methods in the numerical solution of Volterra integrodifferential equations. Journal of Numerical Analysis 2: 21-35.
- Mehdiyeva G, Imanova M, Ibrahimov V (2013) On Research of Hybrid Methods. Numerical Analysis and Its Applications: 395-402.
- Areo EA, RA Ademiluyi, Babatola PO (2008) Accurate collocation multistep method for integration of first order ordinary differential equations J of Modern Math and Statistics 2(1): 1-6.
- G Dahlquist (1959) Stability and Error Bounds in the Numerical Integration of Ordinary Differential Equations. Trans. Of the Royal Inst of Techn Stockholm Sweden Di 87: 3-87.
- Kobza J (1975) Second derivative methods of Adams type Applikace Mathematicky 20: 389-405.
- Iserles A, Norset SP (1987) Two-step method and Bi-orthogonality. Math of Comput 180: 543-552.
- Mehdiyeva G, Imanova M, Ibrahimov V (2013) A way to construct an algorithm that uses hybrid methods. Applied Mathematical Sciences 7(98): 4875-4890.
- Hairier E, Norsett SP, Wanner G Solving ordinary differential equations.
- Mehdiyeva G, Imanova M, Ibrahimov V (2013) A method for solving nonlinear volterra integral equation. Advances in Dynamical Systems and Applications 8(2): 269-280.
- Borrelli RL, Coleman CS (1998) Differential Equations. John Wiley & Sons, Inc: 706.
- Danea S, Codreanu S, Bako B (1997) Detailed analysis of a nonlinear Prey-predator model, Journal of Biological Physic 23: 11-20.
- Ibrahimov VR (1983) On the way for construction of A-stable methods, Approximate methods for solving differential and integral equations, Azer. State University Baku: 55-62.
- Ibrahimov VR (1983) On the way for construction A-stable methods with the high accurary, problem of Automatic control system. Azer.State University, Baku: 86-96.
- Saito Y (2022) biomarker of neurodegenerative disease using diffusion magnetir 17(5): 59-64.
- Resonance Imaging, Mocombe PC (2022) The mathematics of consicouses 17(5): 55-57.
- Emrah Kostem, Eleazar Eskin (2013) Model Discrimination in Dynamic Molecular Systems: Application to Parotid De-differentiation Network. J Comput Biol 20 (7): 524-539.
- Jajjik Kim, Jiaxu Li, SG Venkatesh, Douglas SD, Grzegorz AR, et al. (2013) Model Discrimination in Dynamic Molecular Systems: Application to Parotid De-differentiation Network J Comput Biol 20(7): 524-539.




 We use cookies to ensure you get the best experience on our website.
We use cookies to ensure you get the best experience on our website.