On the Interaction of Viruses with the Immune System

Short Communication

We consider infectious diseases as a conflict between the population of causative agents of the disease and the immune system of the organism. A simple mathematical model can be useful for better understanding of the disease and the formation of drug therapy used for its treatment. We study the mathematical model proposed in [1]. Earlier, the same model was obtained in [2]. In [1], the authors used quite general assumptions. The model has two variables, namely, the population of viruses y and the population of immune cells : The exact identity of immune cells remains open. It is assumed that the degree of immune response depends on the viral load and that the immune response inhibits the growth of the population of viruses. Hence, immune cells may correspond to any branch of the adaptive immune system. Thus, these cells may include the CD4 cells (they are also called T4 cells), i.e., auxiliary cells participating in the attack against infections and the CD8 (T8) cells, i.e., suppressor cells that complete the immune response. The CD8+ cells may also play the role of killers that kill cancer cells and other cells infected by the viruses. The mathematical model takes the form of the following couple of differential equations:

The population of viruses grows at a rate described by the function gr(y) . This function depends on the amount of viruses y and the parameter r that determines the rate of replication of viruses.

The repro- duction (replication) of viruses is the process in the course of which a virus reproduces its descendants (similar to the original virus) by using its own genetic material and the synthetic apparatus of the host cell. The population of viruses is suppressed by the immune response at a rate pyz ; where p is a positive constant. The immune expansion is determined by the viral load y and described by the function f(y) . In [1], it was shown that the functions gr(y) and f(y) must satisfy the following conditions:

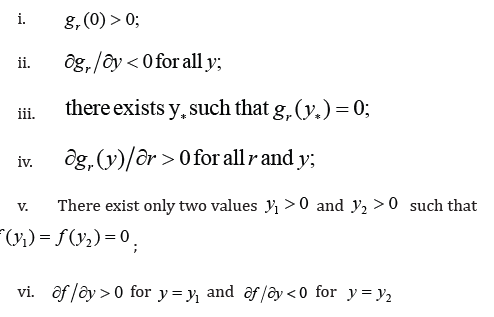
As an example of system satisfying the conditions formulated above, the authors of [1] proposed to use a system

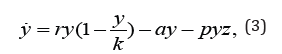
The population of viruses grows at a rate ry(1− y/k) . The parameter r determines the replication rate of viruses, while the parameter k specifies the maximum possible number of viruses, i.e., ry(1− y/k) for all y . The population of viruses dies at a rate ay and is suppressed by the immune system with the rate pyz. The rate of grows in the level of immunity is cyz/(1+εy) . Thus, the process of growth of immunity is described by a saturation function relative to the anlyzed population of viruses (as y → ∞ , the function cyz/(1+εy) remains bounded). Immune cells can also be inhibited by viruses with a rate qyz: Finally, in the absence of antigenic stimulation, the immune response decreases at a rate bz . The phase variables y(t) and z(t) in the system of differential equations (3), (4) are nonnegative (otherwise, they do not have biological meaning) and the constants r, k, a, p,c,ε ,q and b are positive. In what follows, we consider only nonnegative solutions of this system. System (3), (4) is, in fact, system (1), (2) in which and f(y) = cy (1+εy)−b . Equating the right-hand sides of Eqs. (3) and (4) to zero, we get the equilibrium positions of this system:

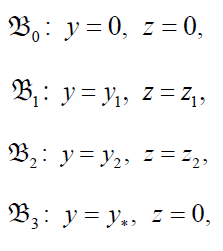
where

The equilibrium position 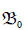corresponds to the absence both of viruses in the host and the immune response to these viruses. In the cases 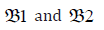viruses and immune cells are balanced, which cor- responds to the chronic cases. Finally, 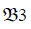corresponds to the case where immune cells are completely suppressed by the viruses. We study the properties of stability of the equilibrium positions of system (3), (4).

Theorem 1: The equilibrium position of system (3), (4) is globally asymptotically stable for r ≤ a and unstable for r > a .

Theorem 2: In the system of differential equations (3), (4), the equilibrium position 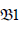is locally asymptotically stable and the equilibrium position 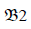is unstable.

Acknowledgement

None.

Conflict of Interest

None.

References

• NL Komarova, E Barnes, P Klenerman, D Wodarz (2003) Boosting immunity by antiviral drag therapy: a simple relationship among timing, efficacy, and success. Proc Natl Acad Sci USA 100(4): 1855-1860.
• RJ Boer, MC Boerlijst (1994) Diversity and virulence thresholds in AIDS Proc Natl Acad Sci USA 91(2): 544-548.