Search for Crucial Events in Physiological Processes

Introduction

This short review is devoted to discussing a still open problem of great importance: to establish with a special method of analysis whether a given physiological process is affected by disease-inducing perturbations. We illustrate the main ideas of the method focusing on a physiological signal of the cardiological processes. The field of research on extreme events is attracting an increasing number of researchers. The idea of extreme events is illustrated in several books [1,2], in publications [3], and in review papers [4,5]. Extreme events may be the results of cooperation between different units of the same system, thereby being a manifestation of self-organization [2]. However extreme events are visible being identified with catastrophes, such as earthquakes and stock market crashes [1]. As clearly stressed in the review paper of [5] the term “extreme event” is commonly adopted to denote unanticipated natural events of perceived high impact.

The definition of extreme events as unpredictable phenomena involves the use of the concept of probability connecting these events with the field of complex networks [3] is a remarkably interesting example of this direction of research. The tools of probability theory are used adopting quantum mechanics and the quantum mechanical transport of information based on the entanglement of quantum bits. This research direction is becoming extremely popular and the very recent review paper of [4] is a remarkably interesting example of this research direction, using quantum mechanical formalism as a fundamental tool. Entanglement, originally proposed by Einstein, Podolsky and Rosen [6] to stress that Quantum Mechanics is an incomplete theory, is now adopted to explain the surprising role of information in the field of Complex Networks.

One important question that we have for the advocates of extreme events is how they can be used to account for the complexity of ECGs and EEGs, which can be easily represented as one-dimensional time series. The main goal of this short review is to prove that the physiological processes are characterized by invisible events, called by us, “crucial events”. These crucial events are often invisible and are not catastrophes. In fact, pathology maybe characterized by the lack of these invisible crucial events.

To understand the importance of crucial events we should introduce our readership to the important property of scaling. The intuitive definition of scaling can be given imagining a runner in the one-dimensional space x. Let us imagine that the runner moves from the origin x = 0 at time t = 0 with velocity . At time t we have x = vt . Let us imagine that the runner makes frequent changes of direction. In this case we have [7], 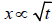. Thus, we can unify these two different conditions with the equation

with δ = 1 when the random walker never changes direction and δ = 0.5, when the random walker changes walking direction in a completely random way. This work is devoted to discussing a condition intermediate between the perfect order, , and the complete disorder, .

The outline of the paper is as follows. Section (II) is devoted to emphasizing the difference between crucial events that are not yet properly considered in the physiological literature and the extreme events that are, on the contrary, attracting an exponentially increasing attention. Section (III) is devoted to illustrating the important tool of Diffusion Entropy Analysis (DEA) that we use to detect crucial events. We devote Section (IV) to discuss a phenomenon of anomalous scaling characterized by the lack of crucial events and we show how to use DEA to prove this important property. Finally, we devote Section (V) to concluding remarks.

Extreme Events and Crucial Events

To afford an intuitive illustration of crucial events, we rest on the fundamental work of Pomeau and Manneville [8]. A Rayleigh-Benard convection is the coordinated movement of a fluid trapped between two thermally conducting plates. The fluid is heated from below. As a result of this heating process when the temperature gradient r is sufficiently large a coordinated motion is generated under the form of either clockwise or counterclockwise regular rotations.

When the control parameter r exceeds a critical value r_T, the regular oscillations are replaced by short bursts of disorder (turbulence). These short bursts of disorder are our crucial events. To facilitate the creation of crucial events, rather than using the popular Manneville map, adopted for instance by Zumofen and Klafter [9] we follow the prescription of [10] called by us idealized version of the Manneville map. We consider the equation of motion

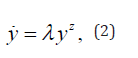
where y is a variable moving in the interval I = [0,1]. The choice of the initial condition is totally random, with the points of this interval sharing the same probability. The particle moves from this initial condition towards y =1 . The time spent by the particle to reach the border is called τ. The process is totally deterministic. Randomness is introduced in this picture by selecting a new random initial condition. With easy analytical calculations we find that the distribution density ψ(τ) gets the inverse power law structure:

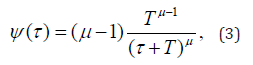
Where

And

The value of the complexity index μ ranges from μ =1 to μ = ∞. However, the values μ = 2 and μ = 3 have a special meaning, connected to the moments

If μ < 2 only the zero-order moment exists, as a consequence of the fact that the waiting time distribution is normalized. If 2 < μ < 3, the first moment is given by

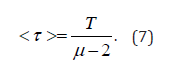
The condition is 3 < μ < 4 characterized by a finite value for both the first and the second moment. For this reason, the condition μ = 3 is frequently considered to be the border between complex and ordinary statistical physics. This is not fully correct as discussed in [11]. A time series {ξ (t)} hosting crucial events does not generate a stationary correlation function 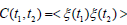, namely correlation functions depending only on . There exist two special values of μ,μ = 2 and μ = 3 . The value μ = 2 is a transition from a regime with μ < 2 , characterized by perennial aging [12], namely, a regime where the correlation function C never becomes stationary to a regime with 2 < μ < 3 , where the correlation function becomes stationary in the long-time limit. Physiological processes are frequently found to work in the regime 2 < μ < 3 [13]. Callum et al. [14] discuss geophysical tremors as dynamical processes occurring in the regime 2 < μ < 3 , thereby sharing the same properties as physiological signals, a condition that may be violated by the extreme events [1].

It is important to stress that the waiting time distribution density of Eq. (3) can be derived directly from the renewal theory of Cox [15], as illustrated in [12]. In his book Cox introduces his readership to crucial events interpreted by him as failure events. A machine created at time t = 0 may fail at time t > 0 . The age dependent failure rate g(t) is defined by Cox as

where Ψ(t) is the time distance between birth ,t = 0 and failure time at t > 0 .

The function Ψ(t) is the corresponding survival probability, namely the probability that no failure has occurred up to a time t,

This makes it possible for us to write g(t) as

yielding

The exponential condition 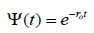is easily derived by assuming that g(t) is constant. Research work fitting the goals of insurance companies seems to be oriented to make the conjecture that g(t) is an exponentially increasing function of time. The research work of our group, on the contrary, focuses on the assumption

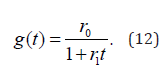
With very simple algebra, we find that Eq. (12) yields the same waiting time distribution density as the idealized Manneville map, Eq. (3) with

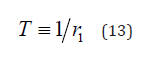
and

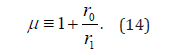
The assumption that g(t) decreases rather than increasing in time is certainly questionable if it is referred to human beings, interpreted as machines designed by engineers. It becomes reasonable and attractive when it is applied to physiological processes. In that case we can interpret the failure as a biological malfunction, instantaneously repaired, a condition that seems to be compatible with the opinion of biologists [16] that the neuron-to-neuron interaction may also involve the instantaneous malfunction repair. In this case a crucial event would be the signature of healthy dynamics, in a striking contrast with the interpretation of a crucial events as a catastrophe. What about the quantum mechanical approach [3,4] to critical phenomena? We believe in the remarks made by Francis Heylighen [17]. This author discusses the Rayleigh-Benard convection phenomenon that we are using to explain the occurrence of crucial events emphasizing the important role of wave function collapses, claiming that it is a mysterious property of quantum mechanics that may be connected to his approach to complexity. We are rephrasing his remarks stressing that crucial events may be a manifestation of wave function collapses.

Diffusion Entropy

To shed light on crucial events, we now describe our proposal to detect them, despite being invisible, a property establishing a striking difference between crucial events and catastrophes. The tool that we propose to detect crucial events is the Diffusion Entropy Analysis (DEA) [18]. The method is based on the observation of a time series ξ(n), the interbeat time between the beat n and the beat n+1. The inter-beat times have a mean value close to 1 second. We plot the difference between the inter-beat time and the mean value, generating the fluctuation process illustrated in Figure 1. We divide the vertical axis into stripes of size s, and we record the time at which the signal enters a given stripe. We focus our attention on the time spent by the signal within a given stripe. The time at which the signal enters a given stripe (or gets out from it) is an event (Figure 1).

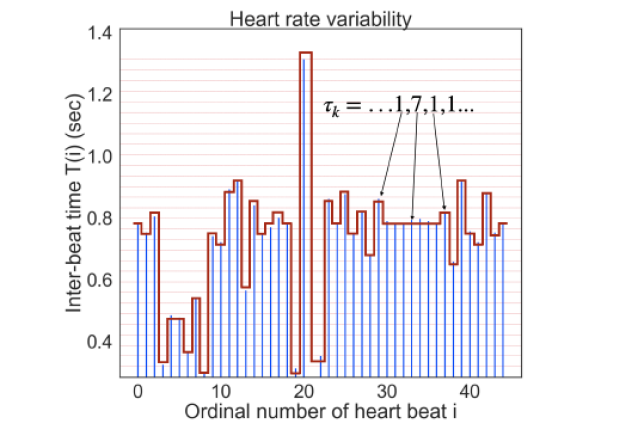
Figure 1: The sequence τ_k is extracted from the inter-beat times by recording the time for which the signal stays in the same stripe. The stripe width used is s= 0.033s.

The time distance between the entrance and the exit time is called τ . If the entrance and exit times are crucial, the corresponding waiting time distribution density is expected to be given by Eq. (3). with 1< μ < 3. The reason for this condition is afforded by [19], which shows that for μ → 3 the scaling δ →0.5. However, we cannot rule out the possibility that also values of μ larger than 3 may generate values of the scaling δ slightly larger than 0.5 because the transition from μ < 3 to μ > 3 is perceived at values of μ slightly larger than 3 [11] as discussed in detail in [14].

We must stress an important issue concerning the size of the stripes that allows us to find the correct scaling. The size of the stripes is a fraction of the span of intensity of the fluctuations. Consequently, some events generated by the crossings of the stripes are not crucial. The time distance between two consecutive non-crucial events is given by an exponential waiting time distribution density and their contribution to scaling is

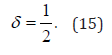
This is a well-known property [20] that can be derived from Eq. (11) by setting g(t) =r₀, namely by assuming that r1 = 0 in Eq. (12). This leads us to reiterate that the crucial events are invisible, namely that the experimental signal illustrated in Figure 1, denoted by the symbol ξ can be written as follows:

The symbol denotes the contribution to the physiological time series generated by non-crucial events, either Poisson or of infinite memory. As we see in IV, the signals with a perennially stationary correlation function do not host crucial events. We assume that the physiological process under study generates a scaling lager than δ = 0.5. In the long-time limit the random walk x(t) obtained by the integration over the experimental time series of Eq. (16)

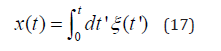
will depart from the origin according to the larger scaling of crucial events. In other words, a representation more accurate of the procedure described in this paper is obtained by replacing Eq. (1) with

Note that

and that the analysis of real cardiological data done in [18] shows that the transition from the healthy to the pathological condition is not signaled only by a small reduction of the scaling δ. It is also signaled by a reduction of p₂ and corresponding increase of p₁ . With this paper we want to attract the attention of the readership with main interest on physiological processes, to the fact that this transition to a pathological condition is not only due to a slight increase of σ_C but also due to an increase of the concentration of non-crucial events, including infinite memory as well as Poisson events.

Note that the research work done by our group on physiological processes led us to the conclusion that 2 < μ < 3 for both ECGs [18] and EEGs [21]. In both cases

which for 2 < μ < 3 makes . This explains why the method of DEA [18] makes it possible to detect the invisible crucial events, which are characterized by a scaling larger than non-crucial events. However, it is to be noted that the method of DEA proves that explaining why the pathological signals are more renewal than the healthy signals.

Anomalous Scaling Without Crucial Events

It is important to stress that the anomalous scaling of Eq. (20) is not limited to ECGs and EEGs. It is a sign of “intelligence” of complex systems ranging from the brain to social systems, generated by the cooperative interaction of their units, [22,23], with 2 < μ < 3 with μ very close to 2. This is in line with the statement that the brain is a source of maximal intelligence, yielding δ =1. Recent work affords support to the conjecture that also the motility of cancer cells shares the condition of intelligence corresponding to 2 < μ < 3 . The work of [24] based on the observation of motility of cancer cells is leading to 2 < μ < 3 , with the preliminary result of μ = 2.5 . The motility of cancer cells is an issue of increasing interest, as shown by the recent paper of [25]. Of course, the use of the statistical analysis proposed by this paper should contribute to the search of a method to kill the intelligence of cancer cells.

To explain this challenging issue, we have to notice that the work of [26,27] shows that the seed germinating in an environment not affording the proper nutrients and the heart of a healthy patient under homeopathic neuropathy of increasing severity makes a transition from a condition hosting crucial events to an anomalous scaling without crucial events. To properly interpreting the nature of this transition we review the theoretical work of our group on the origin of the 1/f noise.

The 1/f spectrum generated by crucial events has the form [12]

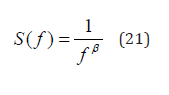
with

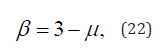
thereby generating 1/f noise when μ = 2 .

As discussed in [26] the FBM 1/f noise is characterized by

thereby generating the ideal 1/f noise when H =1.

(Figure 2)

Figure 2: Shown here is the trajectory of a particle moving freely in 2 dimensions, generated by projecting Fractional Brownian Motion along the X and Y directions.

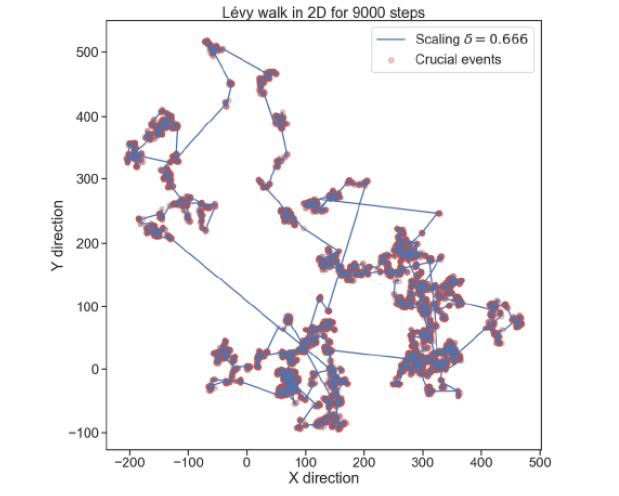
Figure 3: The diffusion generated by a 2-dimensional Levy walker with an inverse power law index μ = 2.5 , simulating the movement of a cancer cell in a 2-dimensional fluid medium.

In the case of physiological processes observed through ECGs and EEGs the transition from anomalous scaling generated by crucial events to anomalous scaling without crucial events is a sign of a pathology that may be cured with non-invasive stimuli inducing crucial events [23]. The theoretical benefit of the observation of the motility of cancer cells with the method of analysis of this paper is that the pathological effects of a transition from a condition dominated by crucial events to an anomalous scaling without crucial events [26,27] may suggest the discovery of a technique to kill the crucial events of cancer cells. Fig, 2 illustrates the motility of a cell with anomalous scaling H = 0.666. This is a motility without crucial events, generated from Fractional Brownian Motion (FBM). This form of infinite memory was proposed by Mandelbrot and Weiss. Our group emphasized the quantum mechanical origin of this form of anomalous scaling and the work of showed that the adoption of DEA [18] with the stripes illustrated in Section III has the effect of killing this form of anomalous diffusion yielding δ = 0.5, proving the lack of intelligence of this form of anomalous diffusion [28-30] (Figure 3).

FBM is a process with infinite memory generated using quantum mechanical arguments [28]. It can be derived from the adoption of quantum mechanical arguments [30]. Thus according to the theoretical proposal of this paper quantum mechanics does not generate complexity, in conflict with the advocates of quantum mechanics [3,4], but an apparent form of complexity, that may be interpreted as a kind of organization collapse. Fig. 3 was generated to mimic the dynamics of cancerous cell [24] if they behave as a Levy walk, whichis a two-dimensional diffusion with crucial events. In the case of Fig. 3, μ = 2.5 . Eq. (20) assigns to this trajectory the same scaling as that of Figure 2, δ = H = 0.666 . The cell moves with constant velocity and from time to time it changes flying direction. It is remarkable that the changes of direction are visible crucial events, becoming invisible when we observe the x and y projections of the trajectory. DEA affords the same results, δ = 0.666 for both directions as well as for the two-dimensional motion.

Concluding Remarks

Crucial events play an important role in the case of ordinary physiological processes. The main role of biomedicine should be to recover the missing crucial events, using non-invasive stimuli, for instance music, rich of crucial events. The fight against cancer should be based on the opposite role of killing the crucial events of the intelligent malignant cells. It is not yet known what the dynamical process is killing crucial events. We are convinced that its discovery will lead also to an efficient method to fight cancer. Another interesting open question is that whether the increase of  may lead to the increase of fbm. We note that according to Sinn [31] the transition of Fractional Brownian Motion from one stripe to the neighbouring stripe is exponential.

Acknowledgments

We thank ARO and NIH for financial support through grant W911NF-23-2-0247 and sub-award GMO:240910 PO: 0000003121.

Conflict of Interest

None.

References

• Didier Sornette (2003) Why Stock Markets Crash? Critical Events in Complex Financial. Princeton University Press, Prince-ton, NJ.
• Didier Sornette (2006) Critical phenomena in natural sciences: chaos, fractals, selforganization and disorder: concepts and tools. Springer Science and Business Media.
• X Meng, X Hu, Y Tian, G Dong, R Lambiotte, et al. (2023) Percolation Theories for Quantum Networks. Entropy 25: 1564.
• J Nokkala, J Piilo, G Bianconi (2023) Complex Quantum Networks: a Topical Review.
• M Stewart, W C Carleton, H S Groucutt (2022) Extreme events in biological, societal, and earth sciences: A systematic review of the literature. Front. Earth Sci 10: 786829.
• A Einstein, A Podolsky, N Rosen (1935) Can quantum-mechanical description of physical reality be considered complete. Physical Review 47: 777.
• Norbert Wiener: Collected Works Mathematical Philosophy and Foundations; Potential Theory; Brownian Movement, Wiener Integrals, Ergodic and Chaos Theories, Turbulence and Statistical Mechanics.
• Y Pomeau, P Manneville (1980) Intermittent Transition to Turbulence in Dissipative Dynamical Systems. Commun Math Phys 74: 189.
• G Zumofen, J Klafter (1993) Scale-invariant motion in intermittent chaotic systems. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics 47. 851.
• P Allegrini, V Benci, P Grigolini, P Hamilton, M Ignaccolo, et al. (2003) Compression and diffusion: a joint approach to detect complexity. Chaos, Solitons and Fractals 15(3): 517-535.
• M Annunziato, P Grigolini (2000) Stochastic versus dynamic approach to levy statistics in the presence of an external pertur- bation. Phys Lett A 269: 31.
• M Lukovic, P Grigolini (2008) Power spectra for both interrupted and perennial aging processes, J. Chem. Phys. 129(18): 184102.
• B J West, P Grigolini, S E Kerick, P J Franaszczuk, K Mahmoodi, et al. (2023) Complexity synchronization of complex networks. Entropy 25(10): 1393.
• C Muir, M Bologna, P Grigolini, Influence of an environment changing in time on Crucial Events: the earthquake prototype. work in preparation.
• D R Cox (1962) Renewal Theory. Chapman and Hall, New York.
• C Moro, A Liebert, C Hamilton, N Pasqual, G Jeffery, et al. (2022) The code of light: do neurons generate light to communicate and repair? Neural Regeneration Research 17(6): 1251-1252.
• F Heylighen (2021) Entanglement, symmetry breaking and collapse: correspondences between quantum and self-organizing dynamics. Foundations of Science 28(1): 85.
• P Allegrini, P Grigolini, P Hamilton, L Palatella, G Raffaelli, et al. (2002) “Memory beyond memory in heat beating, a sign of a healthy physiological condition”, Physical Review E 65: 041926.
• P Grigolini, L Palatella, G Raffaelli (2001) Asymmetric Anomalous Diffusion: an Efficient Way to Detect Memory in Time Series. Fractals 9(4): 439-449.
• M F Shlesinger (1974) Asymptotic Solutions of Continuous-Time Random Walks. J Stat Phys 10: 421-434.
• R Tuladhar, G Bohara, P Grigolini (2018) Meditation-Induced Coherence and Crucial Events. Frontiers in Physiology 9: 626.
• P Allegrini, D Menicucci, R Bedini, L Fronzoni, A Gemignani, et al. (2009) Spontaneous brain activity as a source of ideal 1/f noise. Phys Rev E Stat Nonlin Soft Matter Phys 80(6 Pt 1): 061914.
• P Grigolini (2023) Human Complexity: A Symphony of Vital Rhythms. Chapter 12 of the book” The Patient as a Person”, edited by A. Pingitore and M. Jacono, Springer 131-151.
• Y Shah, L Palatella, K Mahmoodi, M Morelli, G Ferri, et al. Levy walk, criticality, and crucial events in cancer cells. work in preparation.
• A G Nagy, I Szekacs, R Horvarth (2022) Simple and automatic monitoring of cancer cell invasion into an epithelial monolayer using label-free holographic microscopy. Scientific Reports 12: 10111.
• M Benfatto, E Pace, C Curceanu, A Scordo, A Clozza, et al. (2021) Biophotons and Emergence of Quantum Coherence-A Diffusion Entropy Analysis. Entropy, 23(5): 554.
• H F Jelinek, R Tuladhar, G Culbreth, G Bohara, D Cornforth, et al. (2021) Diffusion entropy vs. multiscale and Renyi entropy to detect progression of autonomic neuropathy. Frontiers in Physiology 11: 607324.
• G Culbreth, M Bologna, B J West, P Grigolini (2021) Caputo Fractional Derivative and Quantum-Like Coherence. Entropy 23(2): 211.
• B Mandelbrot, J W Van Ness (1968) Fractional Brownian motions, fractional noises and applications. SIAM Rev 10: 422-437.
• R Cakir, P Grigolini, A Krokhin (2006) Dynamical origin of memory and renewal. Phys Rev E Stat Nonlin Soft Matter Phys 74(2 Pt 1): 021108.
• M Sinn, K Keller (2011) Covariances of zero crossings in Gaussian processes. Theory of Probability and its Applications 55(3O): 485.