Exploratory Report on Data Synchronising Methods to Develop Machine Learning-Based Prediction Models for Multimorbidity

Background

Data science is a rapidly evolving research field that influences analytics, research methods, clinical practice and policies. Access to comprehensive real-world data and gathering life-course research data are primary challenges observed in many disease areas. Existing real-world data can be a rich source of information required to better characterise diseases, generate cohort specifications and understand clinical practice gaps to conduct more precision research that is value-based for healthcare systems. A common challenge linked to real-world and research data is a high rate of missingness. Historically, statistical methods were used to address missing data where possible, but advances in artificial intelligence techniques have provided improved and quicker methods for use. These methods could also be used for predicting disease outcomes, improving diagnostic accuracy and treatment suitability.

These methods can be particularly useful for women’s health conditions, where the complex physical and mental health symptoms can give rise to insufficient understanding of disease pathophysiology and phenotype characteristics that play a vital role in diagnosis, treatment adherence and prevention of secondary or tertiary conditions. One such condition is endometriosis. Endometriosis is complex with an array of physical and psychological symptomatologies, often leading to multimorbidity [1]. Multimorbidity is defined by the presence of two or more conditions in any given individual and therefore could be prevented if the initial conditions are managed more effectively. The incidence of multimorbidity has increased with a rising ageing population, burden of non-communicable diseases in general and mental ill health which, is particularly important for women [2]. Another important aspect of multimorbidity is disease sequalae, where a physical manifestation could correlate with a mental health impact, and vice versa. The precise causation is complex to assess due to limitations in the current understanding of disease sequalae pathophysiology [3]. As such, multimorbidity could be deemed highly heterogeneous. Multimorbidity impacts people of all ages, although current evidence suggests it is more common among women than men, even though previously, multimorbidity was thought to have been more common in older adults with a high frailty index score [4]. Hence, multimorbidity is challenging to treat, and there remains a paucity of research available to better understand the basic science behind the complex mechanisms that could enable better diagnosis and management long-term [4].

This undercurrent of disease complexities linked to endometriosis that could lead to multimorbidity should be explored to support clinicians and healthcare organisations in future-proofing patient care [5]. In line with this, exploring machine learning as a technique in conjunction with synthetic data methods could demonstrate better predictions and offer a new solution to sample size challenges.

Methods

Our primary aim of the study was to develop an exploratory machine learning model that can predict multimorbidity among endometriosis women using both real-world and synthetic data. In certain instances, real-world data may present confidentiality issues, particularly in medical research where data often contains personal and sensitive information. Sharing such data for analysis can expose vulnerabilities. To develop these models, existing knowledge and symptomatology, comorbidities and demographic data were used. Anonymised data from an ethically approved study was provided from Manchester and Liverpool Endometriosis specialist centres in the UK. The data records used included symptoms, diseases, and conditions in women with a confirmed diagnosis of endometriosis. Data curation was completed for the entire sample size using the following steps;

Data Pre-Processing: the data was cleaned and prepared to manage missing values, encoding categorical variables, and standardizing or normalizing continuous variables.

Synthetic Data Generation: the synthetic data records were generated for each centre using a widely used synthetic Data Vault's Gaussian Copula model, based on the data characteristics from patients' records.

Model Development: trained and implemented four standard classification models - Logistic Regression (LR), Support Vector Machine (SVM), Random Forest (RF) and Gradient Boosting (GB) - on both real-world and synthetic data. These models were used to predict multimorbidity among women with endometriosis.

Model Evaluation: models were assessed the performance of the models by comparing their average accuracies on real-world and synthetic data. Metrics’ of accuracy, and Area Under the Receiver Operating Characteristic Curve (AUC) were used to evaluate the models' performances.

Comparison and Analysis: the results of the models trained on real-world data and synthetic data to determine if synthetic data could serve as a viable alternative for real-world data in predicting multimorbidity among women with endometriosis.

For all experiments, we train models on both real-world data, synthetic data. Both types of models were tested on the same test sets which contained only real-world data because the overall population’s true distribution for endometriosis is verified. The accuracies of these models can then provide better insight into whether the use of synthetic data affects the performance of machine learning models.

Ethics approval

Anonymous data used in this study was approved by the North of Scotland Research Ethics Committee 2 (LREC: 17/NS/0070) for the RLS study conducted at the University of Liverpool.

The model used age, height, symptoms, commodities and weight in a mathematical formulation. Let x_i be the vector containing these recordings for the i^th person and let 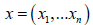be the matrix containing the data about all n people. As part of developing methodological rigour, we considered a working example was used to predict whether each person in the sample develops depression. Let be the vector of response variables where:

In this example, s we collect data for n=3 people and have p=3 recordings for each person (i.e., age, height and weight), These are represented by and 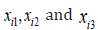respectively. The data can be summarised in Table 1 as follows:

Table 1: Example Dataset for Predicting Depression.

We created a function, f_β with parameters β, that takes the age, height and weight 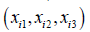of the person i, as input and outputs a prediction of whether they will develop depression. Let y∗_i be the prediction of whether person i develops depression, then we say that

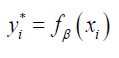
The performance of parameters β can be tested through a loss function, defined as L(β) which measures the difference between the true values of y and the predictions, 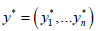. The loss function imposes a penalty when incorrect predictions are made. Hence, to find the best β, we solve the optimisation problem:

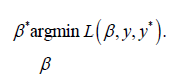
The function f_β∗ can then be used to make predictions for patients who haven’t been tested for depression.

An initial observation was that our prediction function could become over-fitted to the data. This meant that the function captured the specific distribution between x and y very well, but if this data was not in a structured format of the true distribution between symptoms and comorbidities, the prediction function would not be generalisable to other types of data.

The performance of the prediction function on unseen data can be estimated by separating the data into a training set(x^train , y^train ), and test set (x^test , y^test) . The optimal parameters are found using the training set and then the model’s accuracy is tested on the test set. This accuracy is measured by the proportion of correctly classified data. This is measured by a confusion matrix, which records the frequencies of each possible outcome. Let c be the confusion matrix defined as:

where c_ij is the number of times y^test = i while y^test∗ = j . The accuracy of our model is then

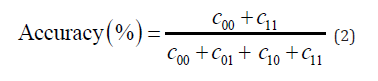
To summarise, the approach is broken down into the following three steps,

1. Solve optimisation problem

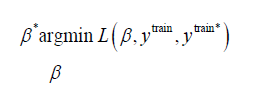
on the training set, where the set of prediction values, y^train*, is found by

Make predictions on the test set using optimal weights β^*

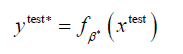
Construct confusion matrix, C as is defined in (1) and find the accuracy of the model on unseen data by equation (2).

Data Preparation-Manchester

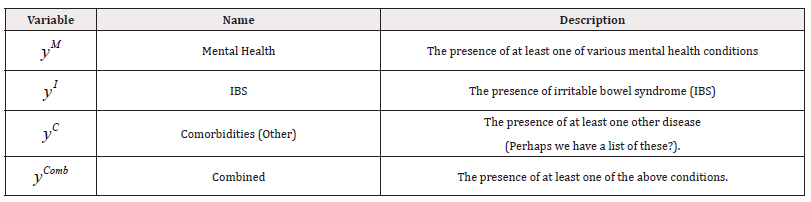
In the Manchester dataset, for each patient, the presence of various symptoms and multiple diagnoses among women with Endometriosis. These are summarised, with descriptions in Table 2. A total of p =15 recordings are made for each person and so we define to be the vector containing the recordings for person i (Table 2).

Table 2: Manchester Data Feature Variables.

Table 3: Manchester Data Response Variables.

Additionally, for each individual, three response variables are documented, which are summarised, along with their descriptions, in Table 3. These variables are defined as follows:

(Table 3).

We examined three models of fit, one for each response variable. We defined a fourth response variable, “Combined”, as shown in the final row of Table 3, which indicates the presence of at least one of the other three conditions. Formally, y^Comb is defined as:

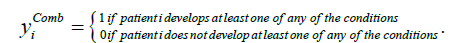
We fitted a fourth model for this response variable.

We converted the binary variables, including our response variables of “Yes” and “No” to 1 and 0, respectively. There was no missing data in the Manchester dataset and as such we make use of all n = 99 observations.

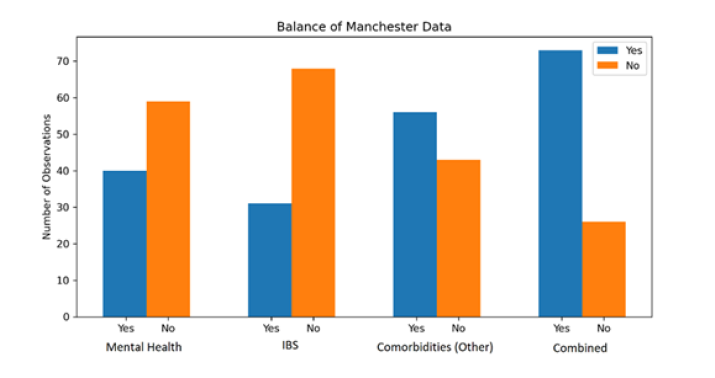
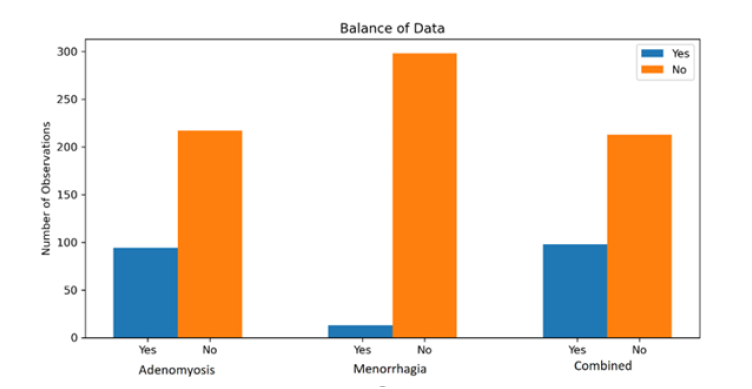
In Figure 1, we studied the balance of the data for each response variable. We can see that Mental Health and IBS, and Combined in particular, suffer quite a large imbalance. To address this, we balanced the data through over-sampling before models were fit (Figure 1).

Figure 1:

Data Preparation-Liverpool

The data from Liverpool had a sample size of 913 patients. The raw data defined 68 possible different symptoms which was considered as feature variables. A significant rate of missing data was identified. The complete list of features along with their percentage missing values can be found in Table 4.

To prepare the data, we first filtered by “Endometriosis = TRUE”, to find only those patients who have already been diagnosed with Endometriosis, leaving us with 339 patients. Next, we removed all features with more than 10% of missing values, leaving us with features. The feature “Endometriosis” is a binary identifier, which, after filtering, is always true, so we dropped this feature too. The final features are summarised, with descriptions, in Table 5. (Table 4,5).

Table 4: Liverpool Data Percentage Missing Data.

Table 5: Liverpool Data Features with Less than 1% Missing Data.

Missing values in these data can were found in Age, Height, Weight, BMI, Sample Type and Parity. Some data with the features Height, Weight and BMI could be calculated from the existing data. Using the formula 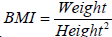, we can compute missing values where possible. The remaining missing data were imputed using scikit learn’s SimpleImputer and IterativeImputer. IterativeImputer models features with missing values as a function of all other features when imputing. However, this only supports numerical data. Therefore, we imputed the missing values of Age, Height, Weight and BMI using this. For the categorical features, including Sample type and Parity, the more simplistic SimpleImputer was used, which samples when considering only the distribution of the feature that is to be imputed.

We selected two diseases as our response variables for prediction (Table 6). Given our ultimate objective of predicting multimorbidity in patients, we constructed a final response variable, “Combined”, as a binary variable representing the presence of at least one of the other two response variables, akin to the data from Manchester. Their formal definitions of these response variables are as follows:

(Table 6)

Table 6: Liverpool Data – Response Variables.

We studied the balance of the data for each response variable, as shown in figure 2. We can see a large imbalance across all response variables. Over-sampling was used again here to balance the datasets before modelling was applied (Figure 2).

Figure 2:

Synthetic Data

To address this concern, we employed the Synthetic Data Vault (SDV) package in Python to create synthetic data as a substitute and assessed its similarity to the real data. By leveraging other sampling techniques, such as random simulation, the synthetic data could generate a dataset with an expanded sample size that more accurately represents the entire population.

During our data preparation, we eliminated numerous observations due to missing data. The synthetic data generator we use can allow for missing values and will generate missing values in the same proportion as they appear in the real-world data. These missing values are then imputed later.

We utilised SDV’s Gaussian Copula model, which constructs a distribution over the unit cube [0.1]^Ρ from a multivariate normal distribution over R^Ρ by using the probability integral transform. The Gaussian Copula characterises the joint distribution of the random variables representing each feature by analysing the dependencies between their marginal distributions. Once the model is fitted to our data, it can be used to sample additional instances of data.

Manchester Data

We initiated our analysis with the Manchester data, and after fitting the Gaussian Copula to our 99 samples, we generated an additional 1000 samples.

By employing SDV’s SD Metrics library, we were able to evaluate the similarity between the real and synthetic data. We examined how closely the synthetic data relates to the real data in order to determine whether we have adequately captured the true distribution. This assessment involved comparing the distribution similarities across each feature, and we adopted two approaches for this evaluation.

Figure 3: Age distribution shape comparison.

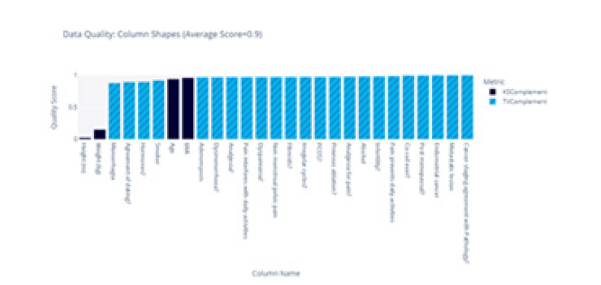
Initially, we measured the similarities across each feature by comparing the shapes of their frequency plots, as illustrated in Figure 3. This comparison was conducted based on the “age” distribution for both the real and synthetic data (Figure 3).

For numerical data, SDV calculated the Kolmogorov-Smirnov (KS) statistic, which is the maximum difference between the cumulative distribution functions. The value of this distance is between 0 and 1 where SDV converted to a score by:

Score =1-KS-statistic

For Boolean data, SDV calculates the Total Variation Distance (TVD) between the real and synthetic data. We determined the frequency of each category value and represented it as a probability. The TVD statistic compares the differences in probabilities, as given by:

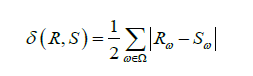
where Ω is the set of possible categories and R_ω and S_ω are the frequencies of category ω in the real and synthetic dataset respectively. The similarity score is then given by:

Score=1−δ (R, S ).

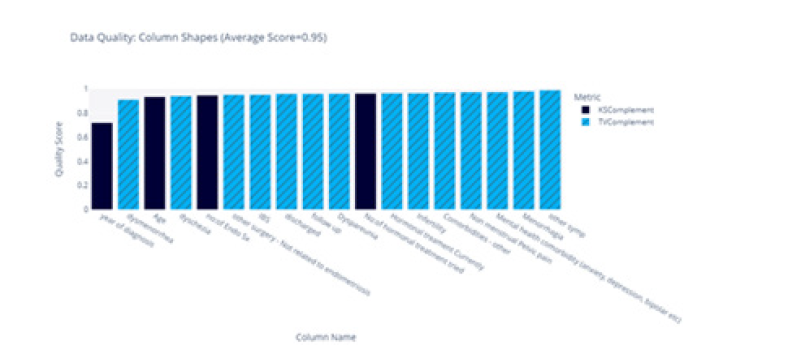
The score for each feature is summarised in Figure 4, and we obtained an average similarity score of 0.92.

Figure 4: Feature Distribution Shape Comparison.

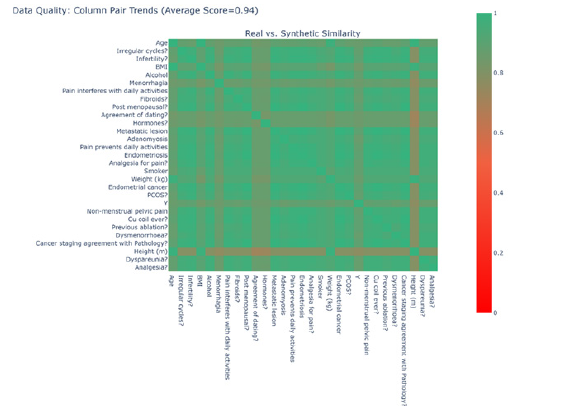
For the second measure of similarity, we constructed a heatmap to compare the distribution across all possible combinations of categorical data. This was accomplished by calculating a score for each combination of categories. To initiate this process, two normalised contingency tables were constructed; one for the real-world data and one for the synthetic data. Let α and β be two features, the contingency tables describe the proportion of rows that have each combination of categories in α and β, thereby illustrating the joint distributions of these categories across the two datasets (Figure 4).

To compare the distributions, SDV calculated the difference between the contingency tables using Total Variation Distance. This distance is subsequently subtracted from 1, implying that a higher score denotes greater similarity. Let A and B be the set of categories in features α and β respectively, the score between features α and β are calculated as follows:

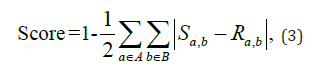
where S_a,b and R_a,b represent the proportions of categories a and b occurring simultaneously, as derived from the contingency tables for the synthetic and real data, respectively. It is important to note that we did not employ a measure of association between features, such as Cramer’s V, since it does not measure the direction of the bias and may consequently yield misleading results.

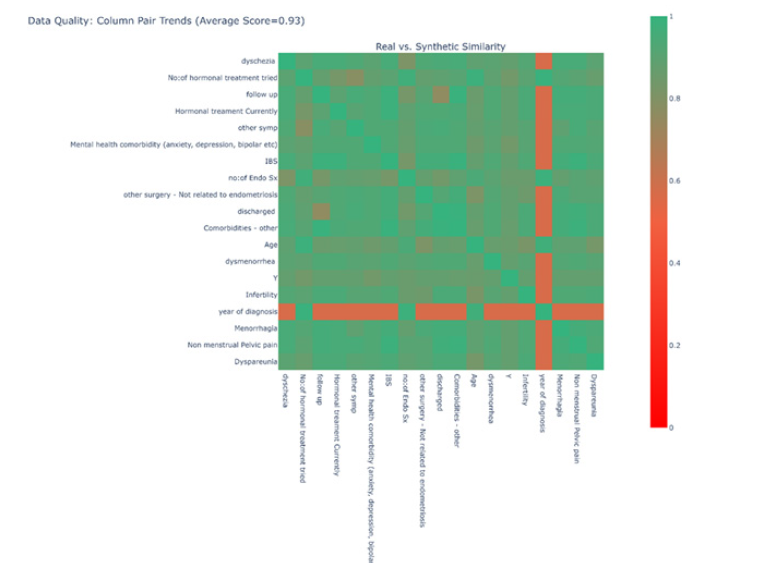
A score of 1 indicates that the contingency table was identical between the two datasets, while a score of 0 indicates that the two datasets were as dissimilar as possible. These scores for all combinations of features are depicted as a heatmap (Figure 5). It is worth noting that continuous features, such as “Age”, were discretized in utilise Equation (3) in determining a score.

The heatmap suggests that most features exhibit a strikingly similar distribution across the two datasets, with the exception for “Year of Diagnosis”. This discrepancy could potentially be attributed to the feature’s inherent nature as a date, despite being treated as an integer in the model. This issue merits further investigation.

Figure 5: Distribution Comparison Heatmap.

Based on these metrics, we confidently concluded, that the new data closely adhered to the distribution of the original data.

Liverpool Data

To generate synthetic data, we adhered to the same procedure as with the Manchester data. We produced 1000 additional samples from a Gaussian copula fitted to the 311 real samples and combined them with the real data to create a new dataset. Using contingency tables, we developed a heatmap by applying the formula in Equation (3) to generate scores; this heatmap is displayed in Figure 6. A score of 1 implies that the contingency table was identical between the two datasets, whereas a score of 0 indicates that the two datasets were as distinct as possible. Our analysis revealed an average similarity of 0.94 (Figure 6).

Figure 6: Real Vs Synthetic Data Distribution Heatmap (Liverpool Data).

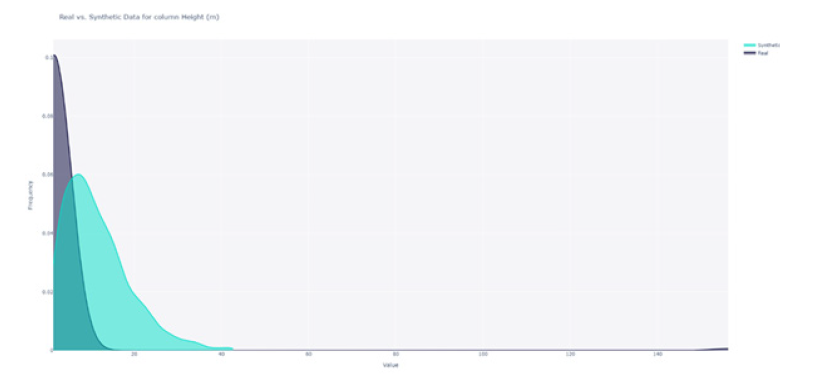
We compared the shape of the distributions for each feature; for instance, the distributions for the “Height” feature are illustrated in Figure 5. We observed that the distributions were dissimilar. To calculate similarity scores, we employed the KS statistic for numerical features and Total Variation Distance for Boolean features. These scores are summarised in Figure 8. We found that the distributions of “Height” and “Weight” were not similar; however, the distributions of the remaining features exhibited similarity. With an average similarity of 0.75, we concluded that the data distributions were, on average similar. The distributions of all categorical features were accurately captured, but two of the continuous features were not (Figure 7,8).

Figure 7: Height Distribution Shape Comparison (Liverpool).

Figure 8: Feature Distribution Shape Comparison Between Real and Synthetic Data (Liverpool).

Models

We evaluated four standard classification models to predict the response variables; Logistic regression (LR), Support Vector Machines (SVM), Random Forest (RF), and Gradient Boosting (GB) as they employ distinct methods data separation and provide unique insights.

Logistic regression enables us to determine the likelihood of each class occurring. It offers straightforward interpretability of the model’s coefficients, allowing us conduct statistical tests on these coefficients to discern which features significantly impact the response variable’s value. While logistic regression adopts a more statistical approach by maximising the conditional likelihood of the training data, SVMs take a more geometric approach, maximising the distance between the hyperplanes that separate the data. We fitted both logistic regression and SVMs to compare the performance of these approaches.

In contrast to SVMs and logistic regression, which attempt to separate the data using a single decision boundary, random forest employ decision trees that partition the decision space into smaller regions using multiple decision boundaries.

The performance of these varies depending on the nature of the data’s separability. Consequently, we fitted all three models and compared their accuracies to assess the useability of the synthetic data.

Logistic Regression

Let 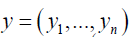to be the general vector of response variables and let 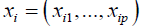be the corresponding vector of features for patient i. We defined the function:

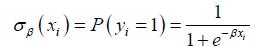
as be the probability of patient i developing the condition corresponding to y, where 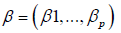are some weights. The prediction function is then defined to be:

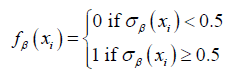
We determined the optimal weights by solving the optimisation problem:

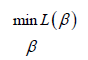
where, for logistic regression, the loss function L took the form:

Finally, we incorporated regularisation terms λ to prevent overfitting, which facilitated capturing the underlying distribution of the data without the proposed model to become overly specific to the training data. This approach helped mitigate any potential biases.

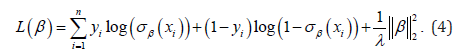
SVMs

Next, we examined Support Vector Machines. We slightly redefined our response variables from binary {0,1} to binary {-1,1}. For instance, suppose 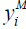represents the binary response for a patient developing a mental health condition; then 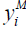is defined as:

For SVMs, the prediction function takes the form:

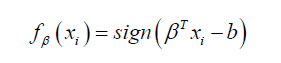
Where 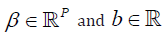are some weights. We considered the hinge loss function, defined as:

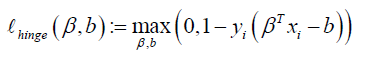
The function 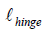is 0 when 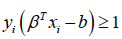, which occurs when 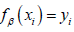or in other words, when we have made a correct prediction. Conversely, when 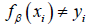, we would incur some penalty. Therefore, for SVMs, the loss function, L takes the form:

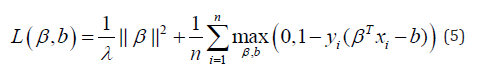
where λ is a parameter controlling the impact the of regularisation term. Similar to logistic regression, this term manages a trade-off between capturing the distribution of the entire population and overfitting to the training data.

Random Forest

The next model we fitted is the random forest predictor. These random forests classify data points through an ensemble of decision trees. The decision trees operate by separating the predictor space by a series of linear boundaries. As before, we let 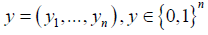be our set of response variables with corresponding feature vectors where each To build our random forest we followed the procedure:

For b =1,..., B :

Sample, with replacement, 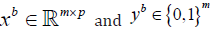from x and y respectively.

Fit k decision trees, to dataset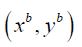

When making predictions on unseen data, the model took the majority vote across all trees.

Gradient Boosting

Finally, we fit Gradient Boosting models to the data which shares some similarities with Random Forest. Similarly, it is an ensemble model, producing a prediction from the ensemble of many weaker predictive decision tree models with the difference that trees are trained sequentially. Random Forest, on the other hand, constructs trees independently.

For all experiments, we run 5-fold cross-validation to test our models. The data were split into a training set and test set before the synthetic data were generated. This allowed us to avoid data leakage, giving a fair comparison between models trained on real-world data and those trained on synthetic data. To further ensure a fair test, the synthetic data were generated before any imputation was done.

All models contain at least one hyper-parameter, and we make use of grid searches to identify the optimal value of these. The result of the best performing model is then presented.

We make use of two measures of performance, the classification accuracy, recording the percentage of correctly classified instances in the test set and the AUC score, which gives an indication of how well the model can distinguish between classes.

Manchester Data

At each fold, the real-world training set contained 80% of the observations (approximately 80 observations), the test set contained 20% (approximately 20 observations) and the synthetic training data contained 1000 generated samples.

Logistic Regression

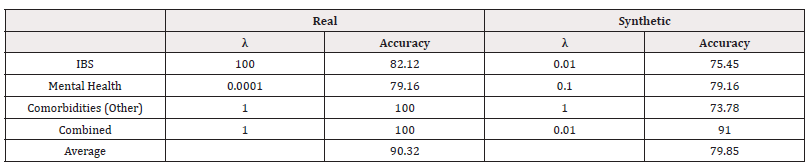
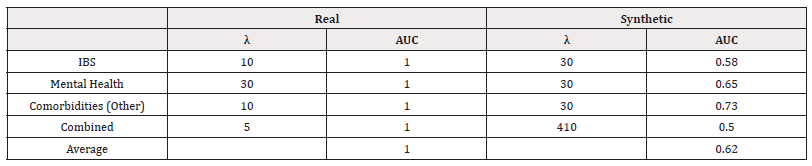
We used scikit-learn to fit logistic regression models of the form in equation (4). We performed a grid search to investigate the optimal value of λ. The accuracies of the best-performing λ for each response variable can be found in Table 7. We also record the Area Under the Receiver Operating Characteristic Curve (AUC) in table 8 (Table 7,8).

Table 7: Logistic Regression Accuracy Comparison Across Real and Synthetic Data.

Table 8: Logistic Regression AUC Comparison Across Real and Synthetic Data.

We can see that for all response variables, in terms of accuracy, the models performed as well as or slightly worse when trained on synthetic data. In terms of AUC, we see the models trained on synthetic data perform worse. The values indicate some poor performance in distinguishing classes.

SVM

We used Scikit-learn’s svm. SVC to train and test SVMs of the form in equation (5) on our data. Scikit-learn is a popular and well-tested choice for SVMs that has shown high performance on a variety of types of datasets.

Similarly, a grid search was performed to find the optimal λ. Table 9 shows the accuracies of the best-performing value of λ for each response. From the accuracy scores, we can see a mixture of performances across both methods. For Mental Health, we see the model trained on synthetic data perform better, however, for the other response variables, we see it perform worse (Table 9).

Table 9: SVM comparison with synthetic data.

Random Forest

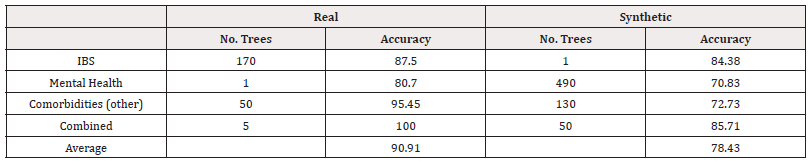
We fitted random forest models to the data. The CV accuracies are summarised in Table 9. Using a grid search, we investigated 1,5,10,20,30,…,500 trees, the accuracy results of the best-performing models are summarised in table 10 with best performing AUC presented in table 11. From both measures of performance, we see the models trained on synthetic data perform worse. The AUC scores in particular suggest poor performance in distinguishing classes (Table 10,11).

Table 10: Random Forest Accuracy Comparison with Synthetic Data.

Table 11: Random Forest AUC Comparison with Synthetic Data.

Gradient Boosting

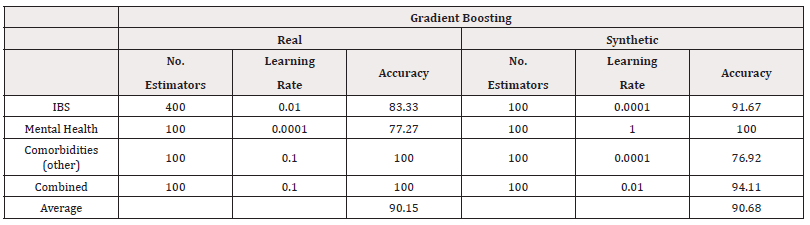
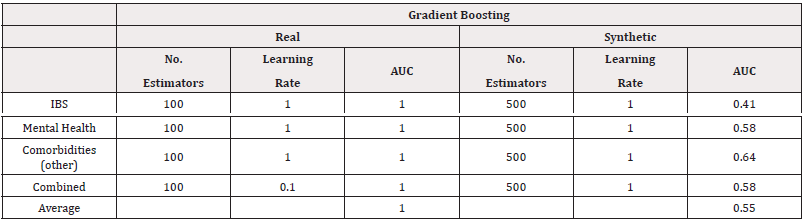
Finally, we fitted Gradient Boost models to the data. Using a grid search, we investigated the optimal combination of number of estimators in the values 100,200,…,500 and learning rate in the values 10^-4,…,10⁰ The results of the best-performing combinations are summarised in table 12. In terms of classification accuracy, we see the synthetic data out-perform the real-world data in the case of predicting Mental Health and IBS. However, the corresponding AUC, as shown in table 13, scores suggest poor performance in distinguishing classes (Table 12,13).

Table 12: Gradient Boosting Accuracy Comparison.

Table 13: Gradient Boosting AUC Comparison.

Upon examining the average accuracies of all our models in Tables 14 and 15, we can draw some conclusions about the performance of the models trained on synthetic data compared to those trained on real data. It is evident that models trained on real-world data performed better than those trained on synthetic data in most cases. However, the performance of the models trained on synthetic data are not significantly worse, suggesting that we don’t compromise a large amount of accuracy. The AUC scores, in some places, suggest a significant compromise in the model’s ability to distinguish classes.

Table 14: Random Forest Model Comparison.

Table 15: Solver AUC Comparison on Manchester Data.

Solver Comparison

In conclusion, the use of synthetic data proves to be a promising approach to training machine learning models when real data is limited or unavailable. The models trained on synthetic data in this study were not always able to out-perform those trained on real data, but they show the ability to retain high levels of accuracy. Many experiments show a classification accuracy of 100%. This is unlikely to happen in reality and suggests that the sample size is too small to make concrete conclusions in some cases. However, some of the findings support the adoption of synthetic data generation methods as a viable alternative to real data in machine learning applications since the loss in accuracy is minimal, and in some cases slightly improves (Tables 14,15).

Sensitivity Analysis

To assess our model’s sensitivity, we introduced random noise to the data and measured the impact on model accuracy. We randomly selected 1% of points in each dataset and replaced their values. Table 16 summarises the accuracy of the new models and the relative percentage change in accuracy (Table 16).

Table 16: Sensitivity Analysis for Models on Manchester Data.

Table 11 reveals that the accuracy of the model was impacted in some instances. The logistic regression model trained on synthetic data was affected by more than 1.7% while the accuracy of its real-world trained counterpart was only changed by 0.19%. Neither dataset shows a consistency to how the models were affected.

Liverpool Results

A similar 5-fold approach was taken to train models on the Liverpool dataset. At each fold, the real-world training set contained 80% of the observations (approximately 271 observations), the test set contained 20% (approximately 67 observations) and the synthetic training data contained 1000 generated samples.

Logistic Regression

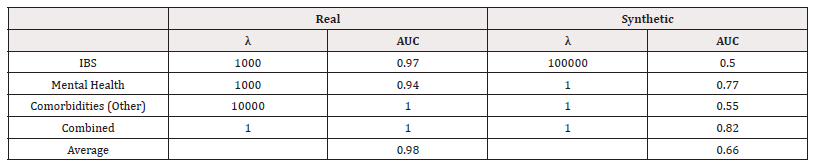
We used scikit-learn to fit logistic regression models of the form in equation (4). We performed a grid search to investigate the optimal value of λ. The accuracies of the best-performing λ for each response variable can be found in Table 17. We also record the Area Under the Receiver Operating Characteristic Curve (AUC) as shown in table 18 (Table 17,18).

Table 17: Logistic Regression Accuracy Comparison.

Table 18: Logistic Regression AUC Comparison.

We see that in all cases of real-world data, the accuracy is recorded at 100%. This is perhaps a consequence of a small sample size. Across all response variables, we see the models trained on synthetic data perform slightly worse. However, the accuracy is not largely compromised.

SVM

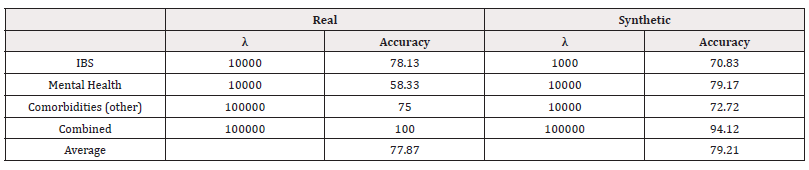
In the same method as in the Manchester data, we train SVMs and compare the accuracy for various values of λ. The best performing models are summarised in table 19.

Table 19: Logistic Regression Accuracy Comparison.

We can see from table 19, that the model trained on synthetic data performed the same or slightly worse than their real-world counter parts. Again supporting the idea that synthetic data may be used as a substitute for real-world data without compromising much accuracy.

Random Forest

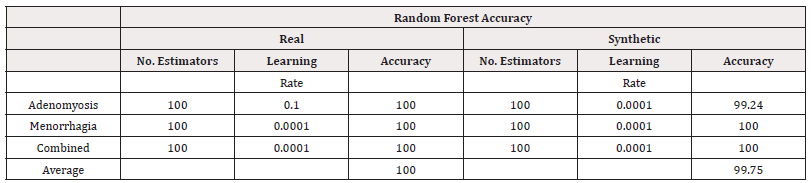
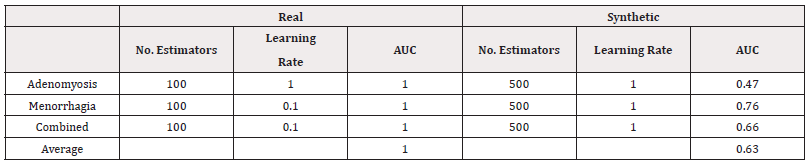
Similarly to the Manchester data, we fitted random forest models, using a grid search to investigate 1,5,10,20,30,…,500 trees. The results of the best-performing models are summarised in table 20 with accuracy scores and table 21 with AUC scores. From both measures of performance, we see the models trained on synthetic data perform worse. The AUC scores in particular suggest some poor performance in distinguishing classes such as for predicting Adenomyosis. However, the results for predicting Menorrhagia support the use of synthetic data, with minimal loss in accuracy and AUC (Table 20,21).

Table 20: Random Forest Accuracy Comparison.

Table 21: Random Forest AUC Comparison.

Gradient Boosting

Finally, we investigated using Gradient Boost models, again using a grid search to investigate the optimal combination of number of estimators in the values 100, 200,…,500 and learning rate in the values 10^-4,…,10⁰

The results of the best-performing combinations are summarised in table 22 for accuracy and table 23 for AUC. The accuracy of the synthetically trained models remain consistent or slightly worse than their real-world counterpart, supporting the use synthetic data without a large loss in accuracy. The AUC scores, however, suggest a larger compromise in distinguishing classes (Tables 22,23).

Table 22: Gradient Boosting Accuracy Comparison.

Table 23: Gradient Boosting AUC Comparison.

Solver Comparison

To summarise, the average accuracies of all models are presented in Table 24, along with their AUC scores in table 25. Overall, the models trained on real-world data performed better. However, the accuracy measures suggest that the use of synthetic data does not significantly impact accuracy performance, while the AUC scores suggest a more significant impact to the ability to distinguish classes (Tables 24,25).

Table 24: Solver Accuracy Comparison on Liverpool Data.

Table 25: Solver AUC Comparison on Liverpool Data.

Sensitivity Analysis

To test the sensitivity of our models we added random noise to the data and measured its impact on model accuracy. By sampling from a unform distribution, we randomly selected 1% of points in each dataset to introduce noise. The values at these points were replaced by random samples from a uniform distribution over the feature’s possible values. Table 26 displays the accuracy of the new models and their relative percentage change in accuracy (Table 26).

Table 26: Sensitivity Analysis on Liverpool Data.

From Table 26, we can observe that the performance of the SVM and Random Forest models experienced minimal change. However, the logistic regression model trained on synthetic data showed a somewhat significant change in accuracy, indicating some sensitivity to perturbations in the data. This suggests that for logistic regression, it is crucial for the synthetic data’s distribution to closely resemble the real data, as the models are sensitive to small variations (Table 27).

Table 27: Comparison of all Models.

Table 27 compares the model accuracies across both datasets. We observed that the models trained on the Liverpool dataset consistently out-perform those trained on the Manchester dataset, for both real and synthetic data.

The two datasets documented different attributes of individuals and contained varying numbers of features and observations. The Liverpool dataset had a larger number of both features and observations, and our method performed well in both datasets. These results support the idea that our method can be applied to a diverse range of datasets. The experiments have also demonstrated the effectiveness our method is with both continuous and categorical data. From the distribution analysis of the Liverpool synthetic data, we observed that our method’s performance was weakest on two continuous features.

Throughout the experiments, we showed that synthetic data performed similarly or slightly worse than those trained on real data. Since all models were tested on real data, this evidence supports the argument that synthetic data can be used as a replacement for real data with minimal compromise on accuracy. However, in some cases, we see a significant compromise in AUC score.

Discussion

Multimorbidity is a growing concern within the global population, particularly for those with chronic conditions like endometriosis, where treatment options are limited. Predicting multimorbidity is challenging among endometriosis patients due to late diagnoses. Therefore, employing machine learning methods to use key features to predict the possibility of multimorbidity is valuable for healthcare services, patients and clinicians. Our findings suggest that the method could be replicated for other complex women’s health conditions such as polycystic ovary syndrome, gestational diabetes or fibroids. 

Our findings indicate that the real-world dataset contained one variable as a significant indicator for developing multimorbidity and highlighted the usefulness of synthetic data for future research, especially in cases with higher rates of missing data. Synthetic data can also provide more detailed information regarding the relationships between these variables, as they could be considered significant indicators. These indicators can be used to differentiate between samples with symptoms and those with disease sequalae that would influence the clinical decision-making process, particularly for patients requiring excision surgery. With a larger sample size and better representation of the overall population, synthetic data has the potential to provide more detailed information about the significance of each feature.

Previous research used methods such as pairwise comparisons to assess diseases in pairs and combined results where appropriate with similar diseases. This technique may have a higher error rate, as complex chronic diseases do not follow a one-size fits-all approach. Whilst the pairwise class of techniques could demonstrate co-occurrence of frequencies and predicted frequencies dissimilar, they can still show a correlation, as indicated by Hidalgo and colleagues’ disease network that represented nodes and edges [6]. This is akin to a network meta-analysis approach. A limitation with this approach in disease prediction could be the lack of temporal data in the resulting network nodes, necessitating an additional analysis such as a correlation evaluation [6]. This also means that data with missing data points may be entirely deleted, impacting the final analysis and any subsequent conclusions. Correlation analyses would enable researchers and clinicians to understand the spread of the diseases based on the links shown within the network that can be modelled over time [6]. Jensen and colleagues demonstrated a similar temporal network approach, showing that a pairwise method can be combined with a correlation analysis over time [7]. Giannoula and colleagues used this approach to reveal disease clusters using a time warping along with a pairwise method to mine multimorbidity patterns and phenotyping with extensive data points [8]. In comparison, our combined approach of machine learning on a synchronised dataset can provide better multimorbidity prediction.

Another class of models used to predict multimorbidity is probabilistic methods, which focus on the relationships among diseases rather than a pairwise approach. Strauss and colleagues employed this method to model a small real-world dataset from the UK evaluating multimorbidity cluster trajectories. Individual patients were grouped in clusters based on the number of chronic conditions detected within their healthcare record over a specific period. These clusters were divided into four main categories, including the presence or absence of chronic problems in the number of comorbidities. However, this approach did not consider patients with undiagnosed symptoms aligned with chronic conditions, which is a common observation in real-world data.

The distribution of the synthetic data captures the true distribution of the real-world data but can have an arbitrary larger sample size, indicating that synthetic data has the potential to provide valuable insight for healthcare services To address the increasing and complex healthcare demands of a growing population, effective clinical service design is crucial for healthcare sustainability., Moreover, our results show that synthetic data accurately represents the real data and so can be used in place of the real data in cases where the real data contains sensitive or private information that cannot be shared. The accuracy measures of our models support the hypothesis that the use of synthetic data does not affect the performance of the prediction models used in this analysis.

Limitations

The model performance will need to be tested on more complex and larger datasets to ensure that a digital clinical trial can be conducted to optimise the model performance.

Conclusion

Our study created an exploratory machine learning model that can predict multimorbidity among endometriosis women using real-world and synthetic data. Before experimenting with the models developed using the real-world dataset, a quality assessment test was conducted by comparing the synthetic and real-world datasets. Distribution and similarity plots suggested that the synthetic data did indeed follow the same distribution as the real-world data. Therefore, synthetic data generation shows great promise, especially for conducting high- quality clinical epidemiology and clinical trials that could devise better precision treatments for endometriosis and, possibly prevent multimorbidity.

Declarations

Conflicts of Interest

PP has received a research grant from Novo Nordisk, Janssen Cilag, and other, educational from the Queen Mary University of London, other from John Wiley & Sons, outside the submitted work.

All other authors report no conflict of interest. The views expressed are those of the authors and not necessarily those of the NHS, the National Institute for Health Research, the Department of Health and Social Care or the Academic institutions.

Availability of Data and Material

The authors will consider sharing the dataset gathered upon receipt of reasonable requests.

Code Availability

The authors will consider sharing the dataset gathered upon receipt of reasonable requests.

Author Contributions

FEINMAN is part of the ELEMI program developed and conceptualised by GD. GD and PP conceptualised and developed work package 1 of the FEINMAN project. GD devised the use of synthetic data to better asses’ chronic diseases. GD devised the hypothesis for using synthetic data modelled on clinical symptoms to develop optimal prediction models. GD, AZ and PP furthered the study protocol. GD developed the method and furthered this with PP, AZ, DB, JQS, HC, DKP and AS. GD, DB, PP and AZ designed and executed the analysis plan. All authors critically appraised, commented and agreed on the final manuscript. All authors approved the final manuscript.

References

• Delanerolle G, Ramakrishnan R, Hapangama D, Zeng Y, Shetty A, et al. (2021) A systematic review and meta-analysis of the Endometriosis and Mental-Health Sequelae; The ELEMI Project. Womens Health (Lond).
• Alimohammadian M, Majidi A, Yaseri M, Ahmadi B, Islami F, et al. (2017) Multimorbidity as an important issue among women: results of a gender difference investigation in a large population-based cross-sectional study in West Asia. BMJ open 7(5): e013548.
• Tripp Reimer T, Williams JK, Gardner SE, Rakel B, Herr K, et al. (2020) An integrated model of multimorbidity and symptom science. Nursing outlook 68(4): 430-439.
• Oni T, McGrath N, BeLue R, Roderick P, Colagiuri S, et al. (2014) Chronic diseases and multi-morbidity-a conceptual modification to the WHO ICCC model for countries in health transition. BMC public health 14(1): 1-7.
• Delanerolle GK, Shetty S, Raymont V (2021) A perspective: use of machine learning models to predict the risk of multimorbidity. LOJ Medical Sciences 5(5).
• Hassaine A, Salimi Khorshidi G, Canoy D, Rahimi K (2020) Untangling the complexity of multimorbidity with machine learning. Mechanisms of ageing and development 190: 111325.
• Jensen AB, Moseley PL, Oprea TI, Ellesøe SG, Eriksson R, et al. (2014) Temporal disease trajectories condensed from population-wide registry data covering 6.2 million patients. Nature communications 5(1): 4022.
• Giannoula A, Gutierrez Sacristán A, Bravo Á, Sanz F, Furlong LI (2018) Identifying temporal patterns in patient disease trajectories using dynamic time warping: A population-based study. Scientific reports 8(1): 1-4.