Research Article 
 Creative Commons, CC-BY
Creative Commons, CC-BY
Useful Generalization of the Inverse Lomax Distribution: Statistical Properties and Application to Lifetime Data
*Corresponding author: Obubu Maxwell, Department of Statistics, Nnamdi Azikiwe University, Awka, Nigeria
Received: November 15, 2019; Published: November 26, 2019;
DOI: 10.34297/AJBSR.2019.06.001040
Abstract
A four-parameter compound continuous distribution for modeling lifetime data known as the Odd Generalized Exponentiated Inverse Lomax distribution was proposed in this study. Basic Structural properties were derived in minute details. Simulation studies was carried out to investigate the behavior of the proposed distribution, from which the maximum likelihood estimates for the true parameters, including the bias and root mean square error (RMSE) were obtained. The proposed model was applied to the strengths of glass fibres dataset and the result compared to other existing distribution.
Keywords: Odd generalized exponentiated family, Inverse lomax distribution, Moments, Reliability function, Hazard function, Continuous distribution
Introduction
Various distributions have been proposed to serve as models for
wide applications on data from different real-life situations through
the extension of existing distribution. This has been achieved in
various ways. The Lomax distribution also called “Pareto type II”
is a special case of the generalized beta distribution of the second
kind [1], and can be seen in many application areas, such as actuarial
science, economics, biological sciences, engineering, lifetime
and reliability modeling and so on [2]. This heavy-duty distribution
is considered useful as an alternative distribution to survival
problems and life-testing in engineering and survival analysis [3].
Inverse Lomax distribution is a member of the inverted family of
distributions and discovered to be very flexible in analyzing situations
with a realized non-monotonic failure rate [4].If a random
variable Χ has a Lomax distribution, then 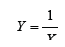 has an inverse
Lomax Distribution. Thus, a random variable X is said to have an In
verted Lomax distribution if the corresponding probability density
function and cumulative density function are given by [5]:
has an inverse
Lomax Distribution. Thus, a random variable X is said to have an In
verted Lomax distribution if the corresponding probability density
function and cumulative density function are given by [5]:
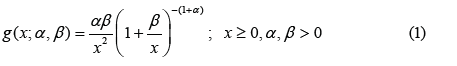
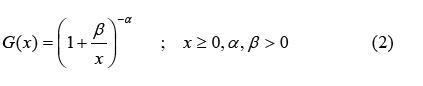
In literature exist several families of distribution and the references to them are listed in [6, 7]. In the course of this study, the Odd Generalized Exponential family of distribution developed by 8 having probability density and cumulative distribution function given by;
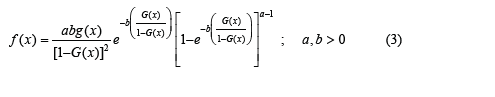

was used to extend the Inverse Lomax distribution. The goal is to derive a continuous compound distribution that would be robust and tractable than the Inverse Lomax distribution. The rest of the article is structured as follows: In section 2, we derive the cumulative distribution function, probability density function, reliability function, odd function, hazard function, reverse hazard function, and cumulative hazard function of the Odd Generalized Exponentiated Inverse Lomax distribution, and present their respective plots for different values of the parameter. In minute details, we establish the structural properties, which include the asymptotic behavior, moments, quantile function, median, Skewness and kurtosis, in section 3. In section 4, we determined the order statistics and the estimate of the unknown parameter using maximum likelihood estimation techniques. Application to two different lifetime dataset and a conclusion is made in section 5.
The Odd Generalized Exponentiated Inverse Lomax (OGE-IL) distribution
A four parameter Odd Generalized Exponentiated Inverse Lomax distribution was investigated in this section. Obtained by substituting equation (2) into (4), the cumulative distribution function of the OGE-IL distribution is given by;
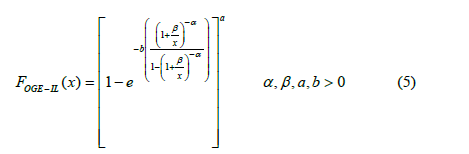
The corresponding probability density function is given by;
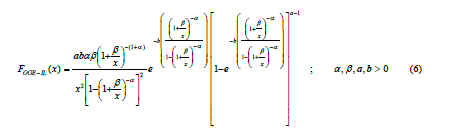
The reliability function is given by;

The failure rate function/hazard function is given by;
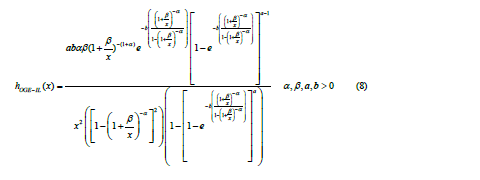
The reverse hazard function is given by;
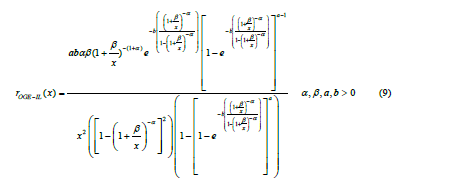
The cumulative hazard function is given by;
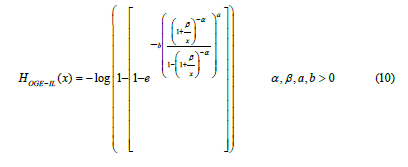
And the odd function is given by;
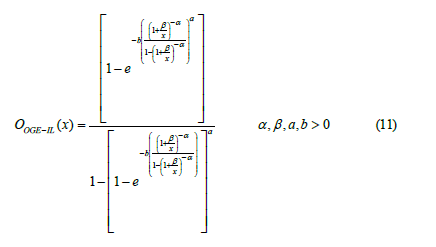
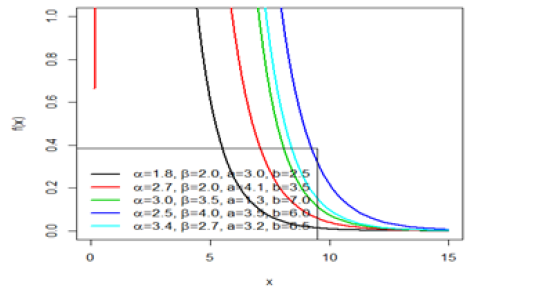
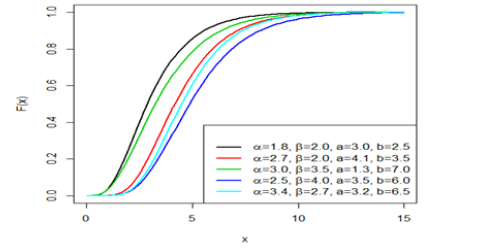
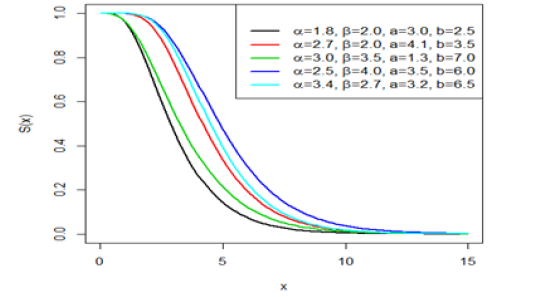
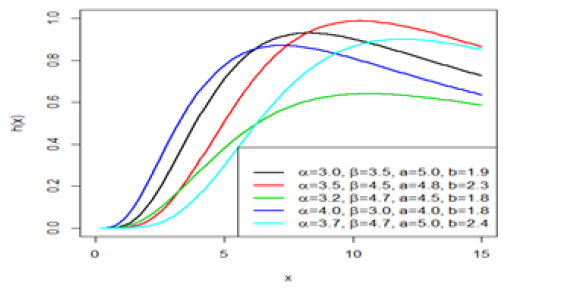
The respective plots of the probability density function, cumulative distribution function, reliability function, and the hazard functions for different parameter values are represented in(Figure 1), (Figure 2), (Figure 3)
Structural Properties of the Odd Generalized Exponentiated Inverse Lomax (OGE-IL) distribution
In this section we derive some of the basic theoretical/structural properties of the OGE-IL distribution, such as; its asymptotic behavior, quantile, median, Skewness and kurtosis of the Odd Generalized Exponentiated Inverse Lomax distribution.
Asymptotic Behavior of the OGE-IL Distribution
We examine the behavior of the OGE-IL distribution in equation (6) as x→0 and as x→∞ and in equation (10) as i.e. x→∞
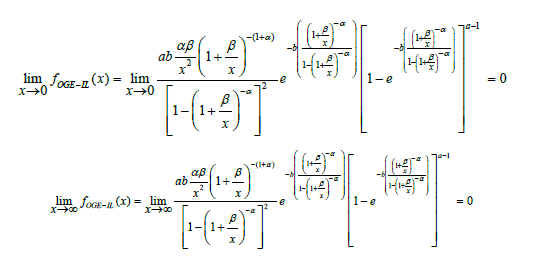
Thus showing that the Odd Generalized Exponentiated Inverse Lomax distribution is unimodal i.e. it has only one mode
We can also deduce that for the OGE-IL Distribution, 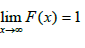 i.e.
i.e.

Thus, indicating that the OGE-IL distribution has a proper probability density function.
Quantile function and Median
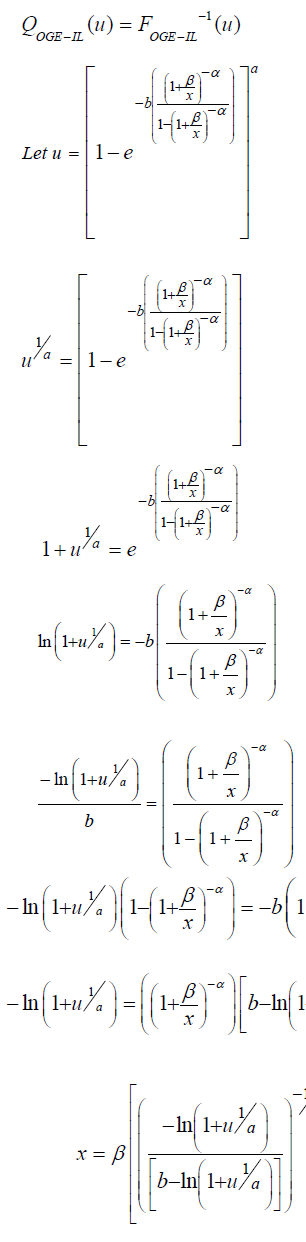
The Quantile function of the Odd Generalized Exponentiated Inverse Lomax distribution is;
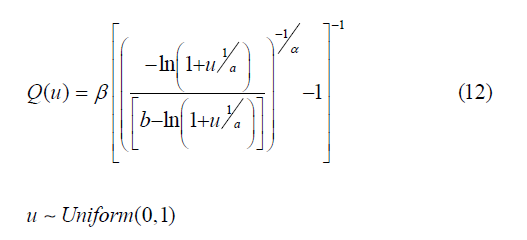
The median of the Odd Generalize Exponentiated Inverse Lomax distribution can be gotten by placing u as 0.5 in equation (12) above, we obtain
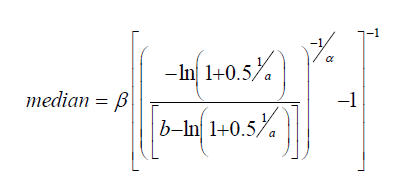
Skewness and kurtosis
According to Kenney and Keeping [9], 9, the Bowely Quartile Skewness is given as;
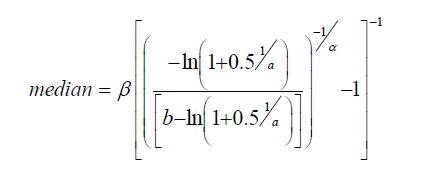
Moors quantile-based Kurtosis by Moors [10], 10 is given as;
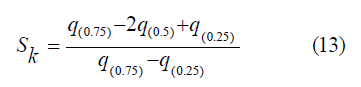
Moment
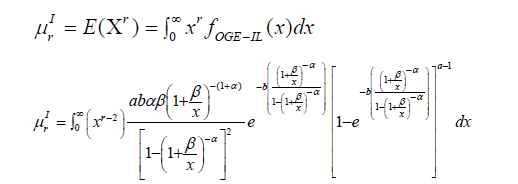
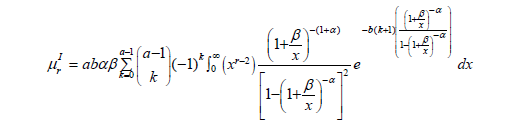
Using binomial expansion and solving through, we obtained an expression for the moment as;
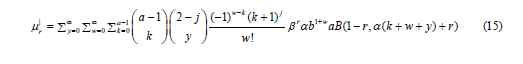
Order Statistics
Consider random sample denoted by 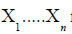 from the densities
of the Odd Generalized Exponentiated Inverse Lomax distribution.
Then,
from the densities
of the Odd Generalized Exponentiated Inverse Lomax distribution.
Then,
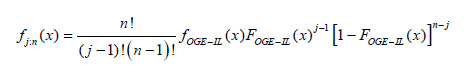
The pdf of the jth order statistics for the OGE-IL distribution is given as;
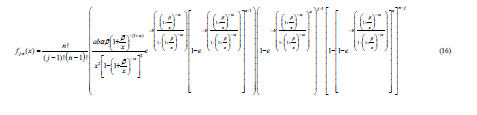
The minimum order statistics for the OGE-IL distribution is given as;

And the maximum order statistics for the OGE-IL distribution is given as;
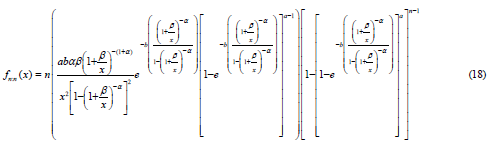
Parameter Estimation
Using maximum likelihood estimation techniques, let 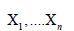 indicate a random sample of the complete OGE-ILD data, and then
the sample’s likelihood function is given as;
indicate a random sample of the complete OGE-ILD data, and then
the sample’s likelihood function is given as;
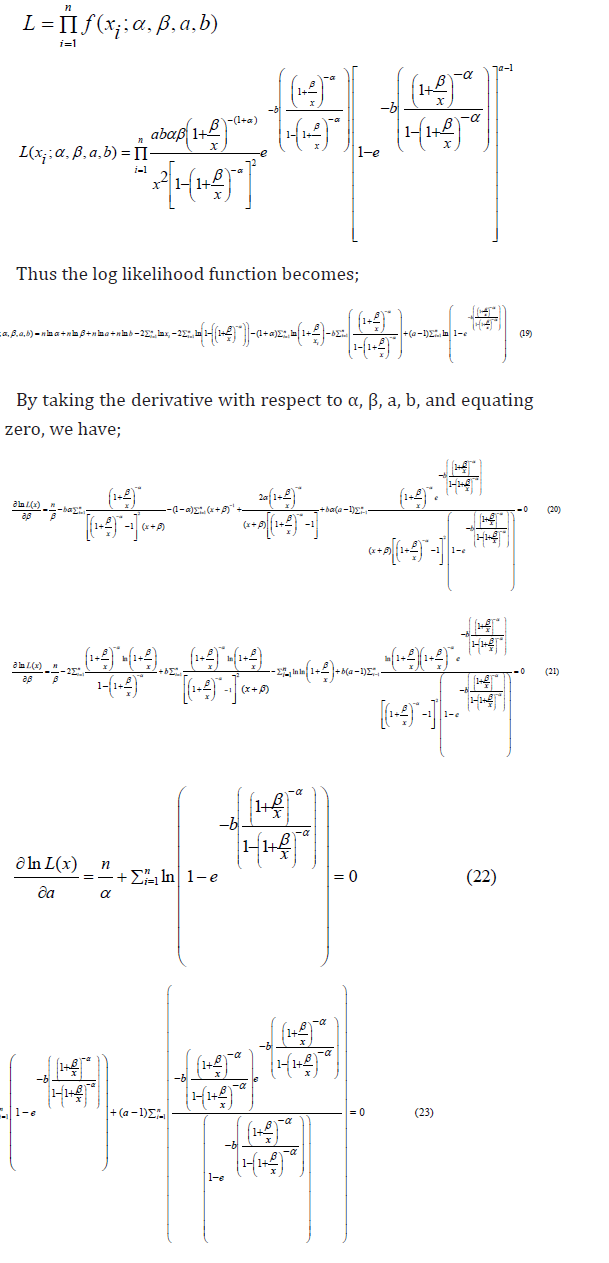
The parameters of the OGE-IL distribution is obtained by solving equation 20-24.
Simulation
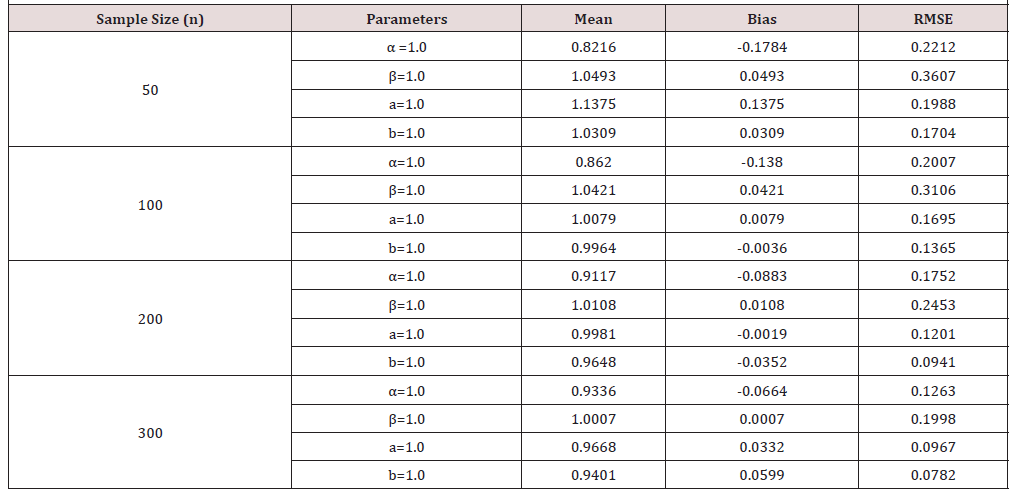
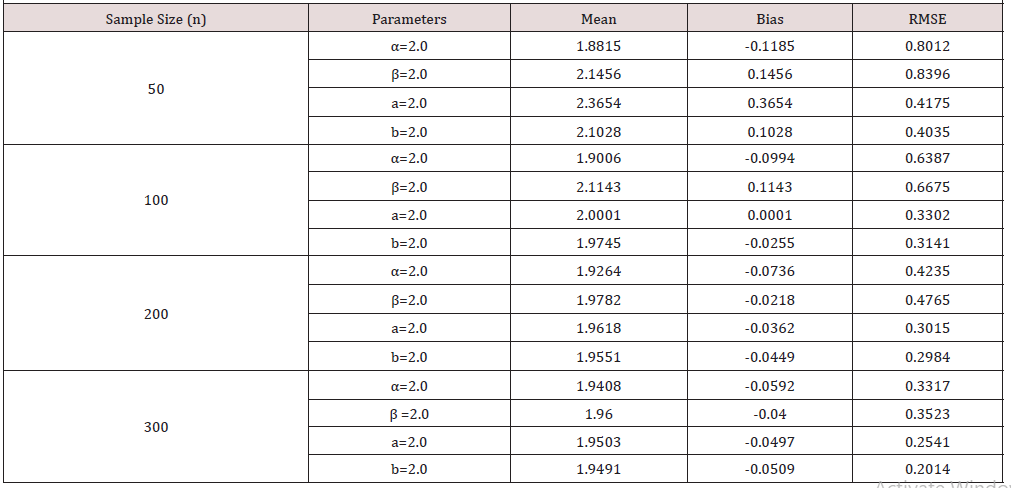
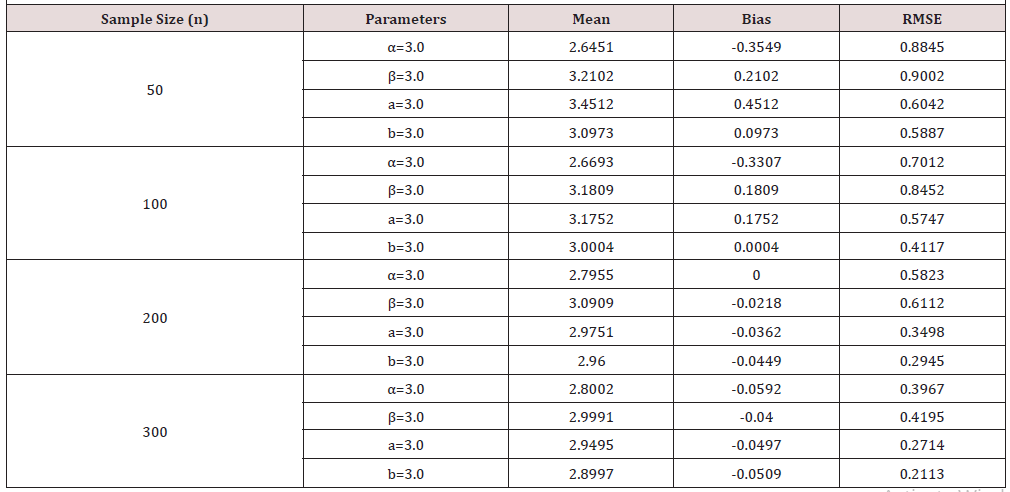
In simulation studies using R software, the behavior of the OGE-IL distribution parameters was investigated. Data sets from the OGE-IL distribution were generated with replication number m=1000, random samples were selected in sizes 50, 100, 200, and 300. The simulation was performed with different true parameter values for four different cases. The selected true parameter values are, α=0.5, β=0.5, a=0.5, and b=0.5; α=1.0, β=1.0, a=1.0, and b=1.0; α=2.0, β=2.0, a=2.0, and b=2.0; α=3.0, β=3.0, a=3.0, and b=3.0 for the first, second, third, and fourth cases, respectively. Maximum likelihood estimates for the true parameters, including the Bias and Root Mean Square Error (RMSE) were obtained. The results of the simulation study are displayed in (Table 1), (Table 2), (Table 3), (Table 4)below.
Tables 1-4 clearly indicate that RMSE decreases when the sample size increases for all selected parameter values. In addition, the variations of the predictions are closer to the actual parameter values, with the increase in the sample size decreasing overall bias. Thus, the estimates tend approaches the true parameter value, as the sample size increases.
Application
The Odd Generalized Exponentiated Inverse Lomax distribution was applied to a real-life dataset and its performance was compared to the Odd Generalized Exponentiated Exponential Distribution (OGE-E) [10, 11, 12], and the Exponential Exponentiated Distribution. The most suitable selection criteria were based on the values of the Log-likelihood, and, Akaike Information Criterion (AIC),
Data I: Strengths of Glass Fibres Dataset
The dataset obtained from Smith and Naylor [13, 14, 15, 16] represents the strengths of 1.5 cm glass fibres, measured at the National Physical Laboratory, England. The observations are as follows;
0.55, 0.93, 1.25, 1.36, 1.49, 1.52, 1.58, 1.61, 1.64, 1.68, 1.73, 1.81, 2.00, 0.74, 1.04, 1.27, 1.39, 1.49, 1.53, 1.59, 1.61, 1.66, 1.68, 1.76, 1.82, 2.01, 0.77, 1.11, 1.28, 1.42, 1.50, 1.54, 1.60, 1.62, 1.66, 1.69, 1.76, 1.84, 2.24, 0.81, 1.13, 1.29, 1.48, 1.50, 1.55, 1.61, 1.62, 1.66, 1.70, 1.77, 1.84, 0.84, 1.24, 1.30, 1.48, 1.51, 1.55, 1.61, 1.63, 1.67, 1.70, 1.78, 1.89.(Table 5), (Table 5)
Conclusion
Using the Odd Generalized Exponential family of distribution, we have successfully extended the Inverse Lomax distribution from a two parameter to a four-parameter distribution. Densities and theoretical characteristics for the proposed OGE-IL distribution have been derived. Simulation studies reveal that the root mean square error decreases for the selected parameter values when the sample size increases. The proposed distribution was applied to a lifetime dataset and compared to other existing distribution which it outperformed based on log-likelihood and AIC values.
Acknowledgement
None
Conflict of Interest
None
References
- Kleiber C, Kotz S (2003) Statistical size distributions in economics and actuarial sciences. John Wiley, Sons Inc, Hoboken, New Jersey.
- B Al Zahrani, M Al Sobhi (2013) On parameters estimation of Lomax distribution under general progressive censoring. Journal of Quality and Survival Engineering 2013: 7.
- A Hassan, A Al Ghamdi (2009) Optimum step stress accelerated life testing for Lomax distribution. Journal of Applied Sciences Research 5: 2153-2164.
- SK Singh, U Singh, D Kumar (2012) Bayes estimators of the survival function and parameters of inverted exponential distribution using informative and non-informative priors. Journal of Statistical computation and simulation 83(12): 2258-2269.
- Yadav AS, Singh SK, Singh U (2016) Bayesian estimation of lomax distribution under type-ii hybrid censored data using lindley’s approximation method. Int Journal of data science 2(4): 352-368.
- Maxwell O, Friday AI, Chukwudike NC, Francis Runyi, Offorha, et al. (2019) A theoretical analysis of the generalized exponentiated inverse Lomax distribution. Biom Biostat Int J 8(1): 17-22.
- Tahir MH, Cordeiro GM, Alizadeh M, Mansoor M, Zubair M, et al. (2015) The Odd Generalized Exponential Family of Distributions with Applications. Journal of Statistical Distributions and Applications 2: 1-28.
- Kenney J, Keeping E (1962) Mathematics of Statistics, Princeton, 1.
- Moors JJA (1998) A quantile alternative for kurtosis. Journal of the Royal Statistical Society 37(1): 25-32.
- Sudhansu S Maiti, Sukanta Pramanik (2015) Odd Generalized Exponentiated Exponential Distribution. Journal of Data Science 13: 733-754.
- Smith RL, Naylor JC (1987) A comparison of maximum likelihood and Bayesian estimators for the three-parameter Weibull distribution. Applied Statistics 36(3): 358-369.
- Maxwell O, Chukwu AU, Oyamakin OS, Khaheel MA (2019) The Marshall-Olkin Inverse Lomax Distribution (MO-ILD) with application on cancer stem cell. Journal of Advances in Mathematics and Computer Science 33(4): 1-12.
- Obubu Maxwell, Samuel Oluwafemi Oyamakin, Eghwerido Joseph Th (2018) The Gompertz Length Biased Exponential Distribution and its application to Uncensored Data. Curr Tre Biosta & Biometr 1(3): 52-57.
- Obubu Maxwell, Oluwafemi Samuel Oyamakin, Angela Chukwu Unna, Adeleke Akinrinade Kayode, Yusuf Olufemi Olusola (2019) On Making an Informed Decision between Four Exponential-based Continuous Compound Distributions. Journal of Advances in Applied Mathematics 4(2): 75-81.
- Obubu Maxwell, Oluwafemi Samuel Oyamakin, Angela Unna Chukwu, Yusuf Olufemi Olusola, Adeleke Akinrinade Kayode (2019) New Generalization of Length Biased Exponential Distribution with Applications. Journal of Advances in Applied Mathematics 4(2): 82-88.
- Obubu M, Nwokike CC, Offorha BC, Olayemi JI, Eghwerido JT (2019) Modeling lifetime data with the generalized exponentiated inverse Lomax distribution. Curr Tre Biosta & Biometr 1(3): 58-61.






 We use cookies to ensure you get the best experience on our website.
We use cookies to ensure you get the best experience on our website.