Ecotoxicology of Altered Fractal Organization in Cells

Introduction

The continuous release of existing and new/exotic chemicals in the biosphere raises concerns for the sustainability of ecosystems. Ecotoxicology is broadly defined as the study of impacts of environmental contaminants to ecosystems (population and community) and organisms. This discipline is relatively new and is confronted to the daunting task of the understanding of toxicity of chemicals and their mixtures in various species of the food chain from bacteria, yeast, cyano/bacteria, algae, the diverse group of invertebrates (worms, micro crustacean, mollusks) and vertebrates. The continuous progression of our technology contributes to the production of new and exotic chemicals that could find their way in various ecosystems with unknown long-term impacts. It is estimated that 84 000 chemicals exist although not all of them are actually marketed (National Academy of Science, 2014). The Society of Chemical Manufactures indicates that at least 25 000 chemicals are produced/used in the commerce [1]. In addition to the “usual” contaminants released in aquatic ecosystems mostly from municipal discharges (i.e., heavy metals, polyaromatic hydrocarbons, pesticides, flame retardants, pesticides), exotic/emerging chemicals such as (new) pharmaceuticals, personal care products, electronics (rare earths for technological devices) and products derived from nanotechnology are also being released in the environment from which long-term effects on ecosystem are not well understood at the present time [2]. The safe and durable management of these substances requires a minimal understanding of their hazards not only individually but in mixtures found in the environment. Hazard assessment requires dose-responses investigations i.e., to determine the dose (concentration) that could lead to harmful effects in a given exposure time frame, and the understanding of the mode of action for prediction. Products from nanotechnology have grown exponentially in the last decades and they are found in many applications as drug vectors, imaging agents, microelectronics, solar energy conversion, fuel additives, paints/dyes and waste remediation technologies. Nanotechnology industry represents between 15-55 billion US dollars market producing in the order of million tons per year of nano products [3]. A corollary to nanoparticle contamination is the production of plastic nanoparticles (NPs) from the degradation of plastic waste. The exponential production of plastic materials has lead to major plastic waste problems and they are now found in nearly all ecosystems of the planet [4]. Indeed, plastic materials are currently found everywhere in the planet even in remote places such as the poles and deep sea abyss. These products can degrade into smaller microplastics and nanoplastics (1-100 nm). Plastic and other NPs are readily internalized in cells [5,6]. These NPs could therefore contaminate the space where essential life-sustaining biochemical processes are at play involving enzymes, membranes and protein networks. A recent study revealed that the infusion of just one plastic tea bag released over 14 billion of plastic NPs finding their way in the drinker’s digestive tract [7]. This raises the question whether plastic NPs reaching the intracellular environment could produce effects resulting from the contamination of the space domain where biochemical reactions are at play.

The cytoplasm is a crowded environment composed of protein networks, enzymes and membranes interfaces. The enzyme lactate dehydrogenase (LDH) could bind to filamentous actin forming an organized structural unit for energy production in low oxygen environments embedded in acting and myosin networks in cells [8]. The estimated protein concentration in the cytoplasm is in the order of 200-400 mg/ml, which can severely limit diffusion of substrates or metabolites. It is anticipated that the addition of other nanosize polymers from nanotechnology could increase again the crowding of the cytoplasm initiating harmful biophysical effects. The understanding on the potential toxic consequences of spatial crowding of local enzymes space domain is thus needed to support risk assessment evaluation of products derived from nanotechnology and plastics.

The space environment of the protein and enzyme networks is organized as fractals similar to a random percolation cluster. A fractal is classically defined as the geometric form reproduced at different scales (scale invariant). Examples of fractals in nature are presented in Figures 1A-C and a percolation cluster is shown in Figure 1D. The repetition of a given form or pattern in space at different scales follow a power law rule: N ~ scalefD where N is the number of pattern or form, fD the fractal dimension and scale. The fD is always smaller than the normal Euclidian dimension (D=3 or 2 for surface), which is a measure of space fragmentation or the dimensionality of space. In crowded environments, enzymes could interact with each other to optimize reaction rates exceeding the constraint of restricted diffusion in crowded intracellular environments [9]. For example, the sequential conversion of fumarate to malate to oxaloacetate to citrate is catalyzed by fumarase, malate dehydrogenase and citrate synthase respectively. These enzymes form temporary (quinternary) structures for optimal reaction rates, which can be isolated using gentle separation and isolation techniques such as gel filtration [10]. These functional units, sometimes coined as metabolons or fluxons, are formed to optimize reaction rates in the fractal organization of the cytoplasm. The tight organisation of these enzymes clusters are supposed to favour channelling of the substrates and products for optimized reaction rates. Thus, the evaluation of enzyme activity in tissue extracts could depend on the fractal organization of protein network and cytoskeleton. In the ecotoxicological context, the evaluation of enzyme activities are often used to diagnose the activation of detoxication, defence or repair mechanisms and health status in organisms exposed to xenobiotics. For example, the evaluation of superoxide dismutase or glutathione S-transferase activities for the elimination of electron radicals and conjugation of polar organic xenobiotics for elimination respectively are often studied in ecotoxicology. These activities are usually determined in subcellular fractions, which includes complex fractal protein networks, albeit diluted in the enzyme assay medium. In the context of NPs or other macrocospic polymers, their impacts on the spatial organization of enzyme activities have yet to be examined.

Figure 1: Fractals in nature and percolation clusters. Examples of natural fractals: a cauliflower A: fiber organization of silk, B: protein networks in cells, C: a random percolation cluster, D: simulating the protein/enzyme organization of the cytoplasm.

Enzyme Behaviour in Fractal Environments

Enzyme kinetics are classically determined in steady state conditions i.e., the initial linear increase in product formation in time is followed in the presence of saturating amounts of substrates. The maintain a constant rate in time, saturating amounts of substrates (maximal velocity or V_Max), usually 5 to 10 times the enzyme affinity constant (K_M) are used. This approach works when “ideal” conditions are met i.e., the enzyme is at least partially purified and diluted in saturated amounts of substrates and cofactors in buffered media where the mass action principle applies. However, enzymes activities are most of the times measured in crowded and complex fractions (supernatants) of cell homogenates. Cellular proteins and enzymes are organized in a fractal manner where the substrates percolate through a complex maze of lattices of proteins (cytoskeletons) as depicted in Figure 1D before reaching the enzyme reaction site [11]. The influence of fractal environments on enzyme reactions have been extensively studied previously by [12,13]. In these conditions, the principle of mass action no longer exists and the fractal organization of space near the enzymes leads to 2 major consequences. The first consequence consists in increased reaction rates than expected at low substrate concentration followed by a decrease in enzyme activity as the concentration increases giving a sigmoidal shape instead of the parabolic shape of the reaction rates versus substrate concentration plot (Figure 2A). This can be explained by the observation that low concentrations of substrates are locally increased in the fractal where the fractal dimension -fD is reduced. As the substrate concentration increases, a traffic-jamming effect decreases enzyme activity than expected by the classical model. The second consequence is that the enzyme kinetic constants (V_Max and K_M) are no longer constants and change in time on a log-log scale (Figure 2B). In this respect, the term constants should be replaced by the term coefficients instead. In fractal environment of proteins, enzyme activity decreases over time with a significant slope h on a log-log scale. Hence in ecotoxicological studies, enzyme activities are determined at high concentration of substrates (jamming effects) and the reaction rates are determined at various time intervals (time influence of enzyme coefficients). The fractal properties of the cytoplasm might influence enzyme activities in the following manner: high concentration of substrate will tend to decrease enzyme reaction rates and depending on the time interval from which the reaction speeds are obtained, the kinetics coefficients (reaction rate) could change. Experiments with various enzymes (LDH, malate dehydrogenase, glutathione S-transferase) measured in homogenate extracts displayed these fractal behaviour [5]. Thus, means to determine the fractal dimension (fD) and other spatial properties would be of value especially when testing for the effects of NPs or other complex polymers that could alter the space organization of the enzyme’s environment. The fractal organization of intracellular space could also influence the oscillatory changes often observed at the biochemical level in cells [14]. Cells could be viewed as scale-invariant (fractal) multioscillator resulting from the complex interrelationships between biochemical processes occurring at the same time in cells. For example, mitochondria are well known oscillator in Ca, citrate and NADH levels [15]. These recurring oscillatory biochemical changes in cells could be altered by changes in the fractal organization of the cytoplasm following a power decay behaviour in the frequency and amplitudes [18]. A consequence of the fractal nature of the space organization of oscillatory changes is the inverse relationship between amplitudes intensity and frequency i.e., increased amplitudes in the changes are found at lower frequencies and inversely (Figure 2C).

Fractal and Spectral Dimensions Analysis of Enzyme Reaction Rates

The fractal dimension fD of complex response patterns could be determined by various methodologies [17]. The rescaled range analysis and the Fourier transformation method for nonlinear and periodic changes in the data were the most reliable to determine the fD. The rescaled range analysis also called the Hurst exponent method is based on the dispersion of the data (scaled with the standard deviation) over time. The disappearance of the substrate (or the formation of product) is followed at each time increments following the relationship: (Max-Min values)/standard deviation = timeH where the H exponent is easily calculated from the log transformation of the equation: log[(Max-Min)/standard deviation)] = H log(t) + log constant. The H value is related to the fD simply by fD=1/H. An H value of 0.5 corresponds to white noise (Brownian motion) and fD=2 corresponding to the normal unrestricted Euclidian dimension. H values> 0.5 indicates that a long term memory effect occurs and reduces the dimension hence the term fractal, while values H<0.5 indicates an oscillatory signal (a succession of high/low changes over time). For oscillatory changes, the Fourier transformation method is the preferred approach to calculate the fD. It is based on the fractal distribution of frequency changes in the following manner: A2 ~ 1/fβ where A is the amplitude, f the frequency and β the fractal exponent. The fractal exponent can be easily calculated from the log transformation: 2log(A) = -β log (f) + log C. The fractal exponent is related to the fD as follows: fD=(3-β)/2 and also to the H exponent: β =2H-1. The square amplitude are obtained by Fourier transformation when generating the periodogram (squares amplitudes for each frequency). Thus, a decrease in the fD will produce more important high amplitude changes but a low frequencies.

The spectral dimension (sD) is another aspect of fractal space but is related to the fD: fD>sD>D (Euclidian). The sD is more related to the topological properties of the crowded space than the local geometric properties of space with the fD. The sD is obtained from the change in enzyme kinetics coefficients over time as shown in Figure 2B. The sD is related to the random walk paradigm in a maze like percolation structure as explained below. In Figure 2B, the slope h is related to the spectral dimension sD by the following h = 1-(sD/2). In unrestricted space, the slope is non-significant (h=0) and the sD corresponds to the Euclidian space of 2 indicating that the enzyme coefficients remain unchanged in time as found in the classical case of uncrowned environments where the principle of mass action applies. The sD is a property of the fractal associated to the random walker problem in a percolation cluster: N(t) ~ t-sD/2 ~1/tsD/2 (Figure 1D). The number of times the walker returns to its point of departure N(t) is proportion to time raised to –sD/2. Thus, if the sD is reduced, it will take less time to the walker (substrate) to return to its point of origin (enzyme) i.e., the enzyme will be visited by the substrate more often. Conversely, if the complexity of the fractal is increased by the percolation structure, the sD will be higher and decreased the number of times the enzyme is visited by the substrate (the speed will be lower). The sD could be viewed as the spreading of the walker in the surrounding space. In the case when h is not significant from 0, sD tends to 2 corresponding to the normal Euclidian space.

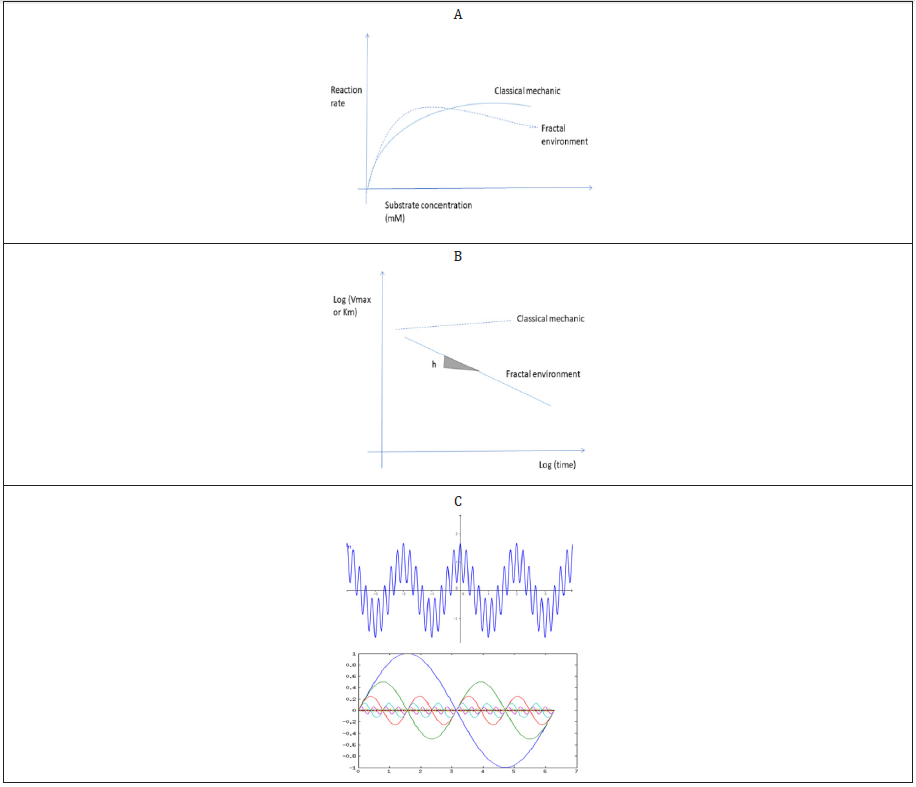
Figure 2: Fractal behaviour of enzyme reactions and oscillators. Crowding effects increase enzyme reaction rates at low substrate concentration followed by a decrease in activity as the concentration increases A: Time dependency effects of enzyme coefficients V_Max or K_M over time, B: Fractal behaviour of sine waves observed in biology, C: where large (small) amplitudes are expressed by low (high) frequencies.

The sD is related to the fD using the following relationship: sD=2fD/wD where wD is the fractal walk which is another fundamental property of fractals [12]. The wD value can also be calculated from sD and fD and is related to distance covered over time: r2=t2/wD where r is the distance covered. Thus, wD is related to the distance covered by the randow walker by opposition to the sD, which is related to the number of times the enzyme is visited in time. When wD decreases, the distance covered is also increased.

Perspectives

Given that the dimension properties (fD, sD and wD) of the fractal space organization could change enzyme activities in complex environments, the contamination of NPs and polymers in proteins and enzymes networks could produce changes in metabolic activity just by changing the fractal properties of the local enzyme environment. In this sense, a local change in the enzyme environment could have broad impacts on enzyme function. For example, the fumarate-malate dehydrogenase-citrate synthase sD of the cluster was increased by neutral polystyrene NPs in vitro and in mussels exposed to NPs and to a municipal effluent, which are suspected source of plastic NPs in the environment [17]. Other studies under way also show that polystyrene NPs could also change the fD of LDH reaction. These studies therefore suggest that measuring enzyme activity under the classical assumptions could lead to misleading results. Enzyme activities obtained in steady state conditions could be “adjusted” for local effects of fractals based on the fD or sD. Because these changes follow a power law approach, enzyme activities are changed in a similar fashion for local effects of the fractal. For the fD, we have v_fD=v^2/fD where v_fD is the enzyme activity adjusted local effects of fD and v is the reaction rate obtained in the classical way (steady-state conditions). The speed of reaction will increase as the fD decreases because the reduced dimension will increase the apparent concentration locally and increase the initial enzyme rates. This satisfy the conditions that when the fD tends to D=2, v_fD=v¹. For the sD, the speed of reaction could be adjusted by the same way: v_sD=v^2/sD. This satisfy the classical situation when sD tends to 2, v_sD=v¹. If the reaction rates decrease in time, the slope h is negative and sD will increase and decrease the reaction rates because the substrates will take more time to reach the enzyme. Conversely, if the slope h is positive, the sD will decrease and increase the reaction rates because the substrate takes less time to visit the enzyme. For example, in a tunnel-like environment of membrane pore, the sD=1 [18,19], which will increase the speed of reaction because the enzyme will be visited by the substrate more often in time. Conversely, in a percolation structure with 59% of space occupied, the sD=1.33, which will lower the speed of reaction because it take more time to the substrate to visit the enzyme. The influence of the spatial organization of enzymes needs to be integrated with enzyme assays determined in the classical way, which do not reflect the behaviour of enzymes in crowded environments in cells. These approaches should provide a more comprehensive interpretation of enzyme activities and metabolism especially in situations where polymers and NPs could influence the spatial properties where these processes are at play.

References

• (2014) SOCMA (Society of Chemical Manufacturers and Affiliates). Myth versus fact about chemicals in commerce.
• Holeton C, Chambers PA, Grace L (2011) Waste water release and its impacts on Canadian Waters. Can J Fish Aquat Sci 68: 1836-1859.
• Inshakova E, Inshakov O (2017) World market for nanomaterials: structure and trends. MATEC Web of Conferences 129: 02013.
• Rhodes CJ (2018) Plastic pollution and potential solutions. 2018 Sci Prog 101(3): 207-260.
• Auclair J, Gagné F (2020) The influence of polystyrene nanoparticles on enzyme clusters of fumarate, malate dehydrogenase and citrate synthase: a fractal analysis study. Lett Appl Nano Bio Sci 9: 981-987.
• Chae Y, An YJ (2017) Effects of micro- and nanoplastics on aquatic ecosystems: Current research trends and perspectives. Mar Pollut Bull 124 : 624-632.
• Hernandez LM, Xu EG, Larsson HCE, Tahara R, Maisuria VB, Tufenkji N (2019) Plastic Tea bags Release Billions of Microparticles and Nanoparticles into Tea. Environ Sci Technol 53(21): 12300-12310.
• Arnold H, Henning R, Pette (1971) Quantitative Comparison of the Binding of Various Glycolytic Enzymes to F‐Actin and the Interaction of Aldolase with G‐Actine. Europ J Biochem 22(1): 121-126.
• Aon MA, Cortassa S (1994) On the fractal nature of cytoplasm. FEBS Letters 344: 1-4.
• Beeckmans S, Kanarek L (1981) Demonstration of Physical Interactions between Consecutive Enzymes of the Citric Acid Cycle and of the Aspartate-Malate Shuttle A Study Involving Fumarase, Malate Dehydrogenase, Citrate Synthase and Aspartate Amino transferase Eur J Biochem 117: 525-537
• Sharma A, Shinde UP, BD Kulkarni (1990) Effect of fractal nature on enzyme reactions Biotechnology Letters 12: 737-742.
• Kopelman R (1988) Fractal reaction kinetics. Science 24(4873):1620-1626.
• Savageau MA (1995) Michaelis-Menten mechanism reconsidered: implications of fractal kinetics. J Theor Biol 176(1): 115-124.
• Lloyd D, Murray DB, Aon MA, Cortassa S, Roussel MR, Beckmann M, Poole RK (2018) Temporal metabolic partitioning of the yeast and protist cellular networks: the cell is a global scale-invariant (fractal or self-similar) multioscillator J Biomed Opt 24(5): 1-17.
• MacDonald MJ, Fahien LA, Buss JD, Hasan NM, Fallon MJ, Kendrick MA (2003) Citrate Oscillates in Liver and Pancreatic Beta Cell Mitochondria and in INS-1 Insulinoma Cells The J Biol Chem 278(51): 51894-51900.
• Schepers HE, HGM van Beek J, Bassingthwaighte JB (2002) Four Methods to Estimate the Fractal Dimension from Self-Affine Signals. IEEE Eng Med Biol Mag 11(2): 57-64.
• Auclair J, Peyrot C, Wilkinson KJ, F Gagné (2020) Biophysical effects of polystyrene nanoparticles on Elliptio complanata Environ Sci Poll Res In press p. 1-10.
• Kopelman R (1986) Rate Processes on Fractals: Theory, Simulations, and Experiments. J Stat Phys 42: 185-200.
• Board on Population Health and Puvblic Health practice (2014) Identifying and Reducing Environmental Health Risks of Chemicals in Our Society: Workshop Summary. Roundtable on Environmental Health Sciences, Research, and Medicine; Institute of Medicine. Washington (DC): National Academies Press, USA.