About Some Applications Multistep Methods with Constant Coefficients to Investigation of Some Biological Problems

Introduction

Noted that many problems from biology were fundamentally studied by Vito Volterra. Model for investigation of these problems compiled using ODEs, Volterra integral and Volterra integro-differential equations. One of the popular methods for solving these tasks is multistep methods with constant coefficients. As is known, one of the basic conceptions in the investigation and application of Multistep Methods with the constant coefficients is its stability. The conception stability for Multistep Method has been defined in two forms. One of these definitions is given by using “ε and δ ” language, which has wide applied in the convergence of numerical sequences. The second definition is related by using stable polynomials and that by some authors has called as the “root condition”. In mostly the second definition has been used in the application of Multistep Methods to solve some problems, such as the initial - value problem for both differential and integra - differential equations of Volterra type. And that also has use in solving of the Volterra integral equations. Here by the comparison of these definition have defined some advantages and disadvantages of them. And has given the way for application of the stable multistep methods to solve of the both Volterra integral and integra - differential equations. The conception of “stability” for the multistep methods with constant coefficients is related with the application of multistep methods to solve initial - value problem for ODE. Therefore, here also to consider the investigation of the conception “stability”. Let us for this began from the following classical problem:

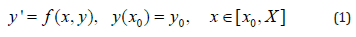
Suppose that the function f (x, y) is continues to totality of arguments and has defined in some cloused domain 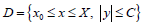And, it has continuously partial derivatives to some integer p in the same domain. It follows that the initial - value problem for ODE has the unique solution on the subsegment 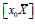, where 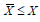Let us suppose that the problem (1) has the unique solution y(x) , which is define on the segment [x0X].

As is known the problem (1) has been investigated by many known scientists such as Newton, et al. Some of them have investigated the construction of numerical methods and their application to solve problems (1) and have considered investigation of Symmetric methods. The first direct method for solving problem (1) was constructed by Euler. The Euler method was developed by Adams and Runge in the results of which appears the multistep and one step methods. By the generalization of these methods the specialists have constructed the class of one step and multistep methods (see for example [1-11]). As was noted above the conception of “stability” is related to the investigation of multistep methods. So as the linear part of one step methods satisfies the condition of stability. Therefore, here as an object of research, were taking the multistep methods with constant coefficients, which can be presented as the following form:

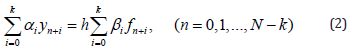
Here ym is the approximately value of the solution y(x) of problem (1) at the point 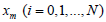But corresponding exact value of the solution of the problem (1) usually is denoted by the 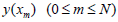The mesh point xm - is determined in the form 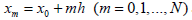. From here receive that 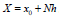. And 0 < h - is the step size, which is divided the segment 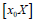to N equal parts. The method (2) has been investigated by many authors (see for example [12-21]).

On the Classification of the Conseptions of Stability

Let us note that method (2) in [12] has investigated by the definition of “stability” using the “ε and δ ” language. It is not difficult to understand that for the investigation of the convergence of the method (2), it is needed to find some concept for boundedness all the errors that are obtained when using this method. In the work [13] have define some condition for limitation of all the errors arises in application of the method (2). For this let us to consider the following definition:

Definition 1. For the limitation of the summarization of all the errors emerging in using of the method (2), the roots of the following polynomial 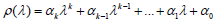must be in the unit circle on the boundary of which are not multiply roots. This conception in [14] and [15] has been taken as the definition of the stability for the multistep methods. In [15] Bakhvalov has investigated the method of (2) for the case βk = 0 = and prove that if the method (2) is stable and has the degree of p , then there exist methods of type (2) having the degree p ≤ k for k ≤10 , but methods with degree p = k +1 are unstable. The conception degree for the method (2) can be given as following form:

Definition 2. The integer variable p is degree of the method (2), if the following is (see for example [15]) take place:

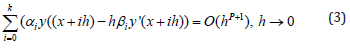
Method (2) fundamentally investigated by Dahlquist. The results obtained by him are use as the Dahlquits law or Dahlquist barer (see for example [14-19]). One of the Dahlquist law can be given as the following form:

Theorem. If in the case αk ≠ 0 and βk = 0, the method (2) is stable and has the degree of p , then the following takes place: p ≤ k .

There exist stable methods with the degree Pmax = k for all the k > 0 .

If αk ≠ 0 and βk ≠ 0 and method of (2) is stable then Dahlquist’s barer can be written as: p ≤ 2[k / 2]+ 2 , there is a stable method with the degree pmax = 2[k / 2]+ 2 for all the k > 0 . As follows from above mentioned, Dahlquist receive more general results than the Bakhvalov and he prove that for all the values of k , there exists stable explicit methods with the degree Pmax = k. Dahlquist also receives some condition imposed on the coefficients of the method (2) in the case when method (2) is convergence. These conditions can be presented in the following form:

a) The coefficients αi, βi ( i = 0,1,...,k ) are the real numbers, moreover αk ≠ 0.

b) The characteristic polynomials

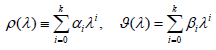
have no common factor different from the constant.

c) p ≥1 and ϑ(1) ≠ 0 are takes place.

By considering the condition C, for the degree of stable methods of type (2) receive the following estimation: 1≤ p ≤ k for explicit and for others 1≤ p ≤ 2[k / 2]+ 2 . If consider that for the explicit stable methods of type (2) the candition p ≤ k is hold, then receive that the condition p > k is hold for the implicit stable methods. As it follows from here, the implicit stable methods are more exact than the explicit methods. But in the application of implicit methods arise some diffucults. To demonostration this, let us consider to following (under the assumption, αê = 1):

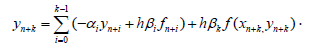
It is follows from here that for the finding the value yn+k, it is nessary to solve nonlinear equation. For this aim one can suggest using some iteration methods. As is known the simple iteration method can be prezented as:

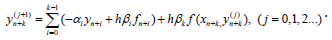
If 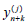is known, then by using this method one can fined the value 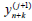. For the calculation of 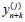can been used corresponding explicit method in the result of which receive predictor-corrector method. This method is fundamentally investigated in [19] and the convergence of the proposed methods are proved.

From this estimation receive that for solving some problems with the higher order of accuracy it is necessary to construct the stable methods with the degree p > 2[k / 2]+ 2 . For this aim some authors proposed to use the following multistep second derivative methods (see for example [20-23]):

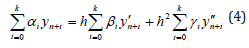
This method in general form has investigated in [22], but in [21] has investigated the convergence of the general form of the method (4) by using “ε and δ” languech. Noted that by using values of the higher derivatives of functions involved in the Taylor expanson in the construction of numerical methods for solving problems (1) suggested by him Euler.

By comparison method (2) and (4) receive that, these methods can be written as the following form respectively:

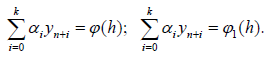
Thus, receive that behavior of the solution of the non-homogenous equation directly dependence on the value of the coefficients αi(i = 0,1,...,k ). It follows that the conception of “stability” for methods (2) and (4) can be defined in the same way. As is known in application of the method (4) to solve the problem (1) are arise some difficulties related with the calculation of the values 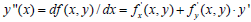. Therefor some authors for the construction of the stable methods with the high order of accuracy proposed to use the forward-jumping or advanced and hybrid methods. For the illustration of noted, let us to consider the following forward-jumping method (see for example [22]):

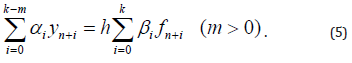
As is known, the advanced methods were constructed by Kowell. But advantages and disadvantages of this method in more general form investigated in [22] and constructed method to eliminate the main disadvantages of these methods. Note that these can be considered better, as in these methods are used information about of the required functions at the previous and at the next points. It is not dificulte to prove that the advanced methods can be prezented only as the implicit methods. In formally this method can been received from the method (2) in the case 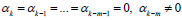. But by the condition of A receive that αk ≠ 0. It is following that method (5) is the independent object for investigation. Noted that if method (5) is stable then exists methods with the degree p = k + m+1 for the k ≥ 3m. But if method (5) is instable, then p ≤ 2k −m is holds. Methods with the maximal degree p = 2k −m is unique. But these properties for the method of (2) can been written as: p ≤ 2k or max p = 2k . Noted that method with degree p = 2k is single.

If will be compare methods (2) and (5), then receive that the maximal value for the stable methods of type (2) dependents from the properties of k . But maximal value for the stable methods of type (4) independent from the properties of k . And now let us consider comparison of the order of accuracy for the method (2) and (4). If method (4) is stable, then there exist the methods with the degree max p = 2k + 2 . Thus, receive that the stable methods of type (2) and (4) with the maximal degree have different properties. Let us to consider the following forward-jumping method, this can receive from the method (4) as the partial case:

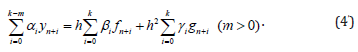
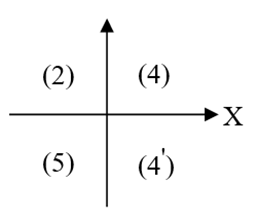
As is known if this method is stable, then following is holds: p ≤ 2k + m+1 for k = 2 j and k −m = 2r −1 (m ≥ 3k) , but in other cases p ≤ 2k + m+ 2 (Figure 1).

Let us compares these results by using x y plane. From here receive that the maximum value for the stable methods of type (4) and (5) do not depend from the property of k and m , but to contrary the maximum value for receiving stable methods from the methods (2) and (4’) depends from the parity of k and m . Thus, got that dependence the maximum value of the degree for stable methods receiving from the above-mentioned methods of the parity of k and m are located symmetrically to starting point of the coordinate system. Noted that if in the method (4) to put γi = 0 (i = 0,1,...,k ), then receive that the degree of stable methods satisfies the condition p ≤ 2[k / 2]+ 2 and there exists the stable methods with the degree p = 2[k / 2]+ 2 for all the value of k .

Figure 1:

Thus receive that the relation between of the degree p and order k for the methods (2) and for the method (4) in the case γ i = 0 (i = 0,1,..., k) are the same. But in the case βi = 0 ( i = 0,1,...,k ) the conceptions of stability and the degree for the method (4) are define in others form. If the following is holds:

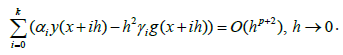
Then the integer value p is called as the degree for the method (4) in the case βi = 0 ( i = 0,1,...,k ).

By taking into account the above-described properties of the methods of type (4), that has investigated in general form in the [22]. Thus, receive that the methods (2), (5) and method (4) in the case βi = 0 ( i = 0,1,...,k ) are independent object for investigation. But there are some connections between of them. For this aim let us to difine direct relation between of the method (2) and the following:

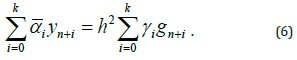
By using the shift operator E y(x) = y(x + h) , equality (6), can been written as following:

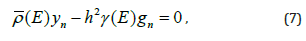
here polynomial 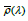and γ (λ ) define as

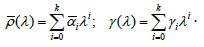
If in the equality of (7) to pass limit, for the h tends to zero ( h→0 ) then receive that 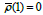. This is a necessary condition for convergence of the method (6). But in future will show that ρ '(1) = 0 . By using the condition ρ (1) = 0 the equality (7) can be written as following:

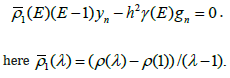
Let us this equality to write in the following form:

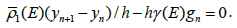
If here to pass limit for the h→0 , then receive:

here x = x0 + nh fixed point.

In the equality of (8), let us use the definition.

y '(x) = z(x) , then from here receive:

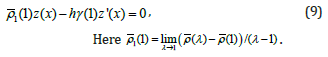
If in the equality of (9) to pass limit for the h→0 , then receive: .

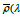It is clear that .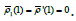

Thus receive 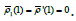, it is to say that λ =1 is the double root for the polynomial 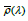. And this condition is necessary for convergence of the method (6). Those, receive that the conception of “stability” for the method of type (6) can been define as following:

Definition. The method (6) is stable, if the roots of the polynomial 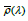Liye in the unit circle on the boundary of which there is not multiple roots, without double root λ =1. If compare method (2) with the method (9), then receive that they are the same. It follows that the maximal value for the degree must be same for these methods. As is known the implicit methods are more accurate than the others. But in the application, to solve the practical problems arises some difficulties which was related with the finding of the solution of nonlinear algebraic equations. As have noted above, for this aim one can use predictor-corrector methods which have been constructed specially for using implicit and forward - jumping methods (see [19]).

It follows noted that predictor-corrector methods are constructed for using the implicit and forward - jumping methods having the different properties. Applications of the forward - jumping or advanced methods are more use information about the solution of the investigated problem at the previous and at the next mesh - points.

Thus, receive that the forward - jumping methods are used the more information about the solution of the investigated problem. Therefor the results received by using these methods can be taken as sufficiently available or these methods can be taken as efficient.

By the comparison of above-described methods receive that the maximal value for the degree of stable methods can been define by the equality pmax = 2k + 2 , which is satisfies for the degree of the method (4). For the construction stable methods with the degree p > 2k + 2 some authors proposed to use the hybrid methods (see for example [23-34]), which in simple form can be written as:

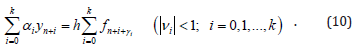
It is known that methods with the fractional step size were always considered better than the others. For example, the following midpoint rool:

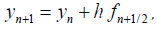
which is explicit and can be received from the method (10), as the partial case. Noted that this method has the degree p = 2 . As is known from the method (2) for the k =1 one can be receive explicit method with the degree pmax =1 and implicit method with the degree pmax = 2 . It is not difficult to prove that following stable method:

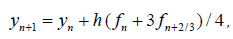
has the degree p = 3 and is also can be receive from the method (10) as partial case.

As was noted above the conception “stability” and “degree” for the method (10) will be defined by the above proposed way. Now let’s consider finding the coefficients of the method (10).

About One Way to Determine the Values of The Coefficients of Multistep Method (10)

By the comparison of the methods (2), (3)-(6) receive that the more interesting methods are the stable methods with the higher degrees. And, have proven that in among of these methods the most accurate is the method (4), the maximal value of the degree, for which is equal to pmax = 2k + 2 . As is known, in the application of these methods to solving nonlinear problems arises some difficulties. By considering this, some specialists proposed to use hybrid methods. Therefore, let us investigate the method (10). For this aim one can use the method of undermined coefficients. For the construction methods of type (10) to consider the following Teylor series:

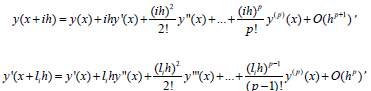
Here õ fixed point and denote as õ = x0 + nh and li = i + vi ( 0,1,2,...,k )

By using this expansion in the equality of (10) receive the following:

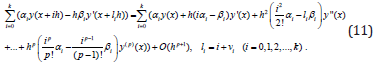
For the finding the maximal value of the degree of the method (10), let us suppous that method (10) has a degree of p . In this case receive the following:

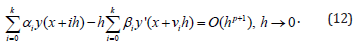
For the finding some relation between of the integer values p and k in the equality of (11) consider the equality of (12). In this case for the holding the equality of (12) receive that the following must be hold:

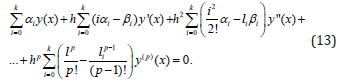
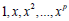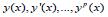It is known that the system or for the 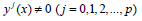are independent. Therefor from the equality of (13) receive that for the holding the equality (12), satisfying following condition the coefficients 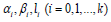is necessary and sufficient:

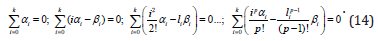
These prove that to, the method (10) to have the degree of p , satisfying its coefficients the system of algebraic equation of (14) is necessary and sufficient. This system is a nonlinear algebraic equation. As is known to find the exact solution of nonlinear system of algebraic equation is available, but not always. Therefore, in basically the scientists for solving of the system (14) are used approximate methods. For example, the case k =1. In this case from the system (14) receive the following:

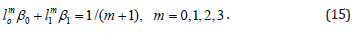
It is not difficult to prove that the solution of the nonlinear system of (15) is unique. And the method of type (10), which is corresponding to this unique solution can be written as following:

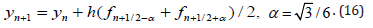
This method stable and has the degree p = 4 . Noted that in the case k = 2 , there is stable method of type (10) with the degree p = 6 . And now let us define the maximal value for the degree of the method (10). It is evident that in the nonlinear system of (14) the amount of the equation equals to p +1, but the amount of the unknowns equals to 3k + 3. It follows that for the p ≤ 3k + 2 , system (14) may have a solution. But the stable method does not correspond to all the solutions of the system (14). If the polynomial ρ (λ ) has the following form

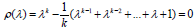or 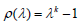then the roots of the ρ (λ ) satisfies the condition: 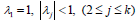or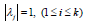

For this polynomial the condition 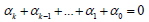is hold. Therefor in this case receive that in the system of (14) will be 2k + 2 unknowns and p-equations. From here it follows that the system for the condition p ≤ 2k + 2 can has any solution. One can be constructing the stable methods of type (10) with the degree p = 2k + 2 for the value k ≥ 3. Noted that method (10) is seems to classical Gauss method. From here receive that method (10) is more general than the Gauss method. It is follows from here that by choosing the coefficients one can be constructed methods with the degree p ≤ 2k + 2 . But for the sake of objectivity remark that in application of hybrid methods to solve some problems arises difficulties related with the computing of the values 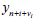for all the 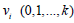. For correction of this disadvantages of hybrid methods, here have proposed to use the predictor-corrector methods.

For construction more exact numerical methods, let us consider the construction methods with the new properties on the intersection of the methods (2) and (10). For this let us to consider the following multistep methods, which has received by using the methods (2) and (10):

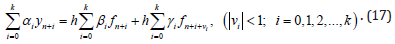
These methods can be written more general form as following:

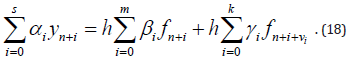
It is evident that in the case s = m = k methods (17) and (18) are one and the same. In the case s < max(m, k) the method (11) will be forward-jumping method, but in the case s > max(m, k) from the (18) receive the explicit methods. For simplicity, here to investigate the method (17). It is not difficult to prove that for the determine the coefficients 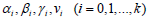can been received the nonlinear system, which is like nonlinear system (14) of algebraic equations. For the construction the concret methods of type (17), let us to consider following system of algebraic equations:

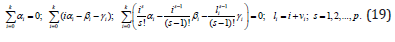
From the nonlinear system of (19) it follows the nonlinear system of (14), as the partial case. Therefore, here to consider the investigation nonlinear system (19). In this system the amount of the equations equal p +1, but the amount of the unknowns is equal to 4k + 4 . In the case p ≤ 4k + 2 the system can have the solution. Noted that in the case γi = 0 ( i = 0,1,2,...,k ) or νi = 0 ( i = 0,1, 2,...,k ), from the method of (17) it follows the method (2), and in this case from the system (19) receive the linear system of algebraic equation, which has a unique solution for the value max p = 2k . But by constructing a method of a certain accuracy, will be shown the exactness stable methods of type (19) with the degree p ≤ 3k + 3. As is known in usually for solving of the system (19) are used some mathematical programs, for example Mathcad-2015. In the result of which one can be received the solution of system (19) in the case p ≤ 4k + 2 .

The results obtained by the application of these methods in solving of some model problems usually are not available. One can be constructed some problem in solving of which the methods with degree p = 0 gives some available results. But it is not following from here, that this method can be applied to solving of the problem (1). As was noted above in solving the system of algebraic equation by using the Mathcad program receive solution with the some errors. Therefor these methods must be verified by the known model problems. And here by considering above described have recommended to use the stable methods of type (17), with the degree p ≤ 3k + 3.

For example let us to consider the following methods:

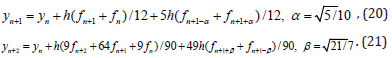
The method (20) is stable and has the degree p = 6 , which receive from the method (17) in the case ê =1, but the stable method (21) received from the method (10) for the ê = 2 and has the degree p = 8 . In this case one can be constructed stable method with the degree p = 9 , but that will not be satisfies Gauss node point condition. Methods (20) and (21) can be taken as symmetric, so as the points and coefficients of these methods satisfies the Gauss conditions.

By comparison of above proposed methods, receive that method of (17) is more accurate than the others, but application that to solve some problems it is arises some difficulties related with the finding the value yn+k , which is also participated under the function of f (x, y) . The second difficulties in application of the method (17) related with the computing of the values of the function y(x) at hybrid points. For example, in the application of the method (16) it is arises the necessary to calculation the values of yn+1/2±α . For using these methods, here have recommended to construct the predictor - corrector methods. But for the finding the values yn+1/2±α one can be proposed some methods specially constructed for computing of the value yn+1/2±α. But in sometimes the hybrid pointes by users can be choose as the rational number. In this case methods will not be more exact, but that can be applied to solving of the some problems in simple form. For the illustration of this result, let us to consider the following methods:

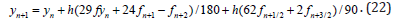
This method belongs to the class of forword-jumring or advanced methods. And the order for which equal two ( k = 2 ), but the value of degree for method (22) equal to five ( p = 5 ). As was noted above in the case k = 2 , one can be constructed stable methods with the degree 5 < p ≤ 9 . But in this case it is necessary to calculate the values of the solution of investigated problem at the irrational points. Noted that in using of method (22) are not arises above mentioned difficulties. In the case γi = 0 or vi = 0 ( i = 0,1,2,...,k ) also are not arise the necessary calculation the values of the function at the hybrid points (usually hybrid points are given by using the irrational numbers). Thus, receive that using rational points in the construction of the numeral methods can be taking as desirable.

Some Advantages of Symmetric Methods

There is such an idea that all Galaxies in the Universe are located symmetrically in relation to each other. The same ideas hold for the planets as well as other celestial bodies. It is no coincidence that in applied sciences highly appreciate the work devoted to the study of symmetric problems. Considering the above described, here also decided to investigate the construction and application of some symmetric methods to solve problems that are being studied here. For receiving some information about the symmetric multistep methods one can used the work [16]. For the sake of objectivity, noted that some of Gauss method can be taken as symmetric (see for example [35-39]).

Bernishteyn has investigated the Gauss and Chebishev methods and fined some symmetric methods. Noted that the symmetric methods are constructed for the case, when the amount of Gauss points are odd. In our case the value of the order for the finite-difference equation of (10) must be even, because the amount of the mesh-point equal to k +1. But these methods can be constructed in the case, when - k is odd. In this case the amount of Gauss points will be even. For the simplicity let us consider compazision symmetric methods of type (2), which has investigated by Dahlquist. For example, let us to consider the case k =1. In this case one can be constructed, the following methods:

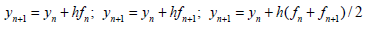
By Dahlquist law receive that trapezoidal method is not symmetric, for which k =1 and pmax = 2 . Definition of the symmetric methods given by Dahlquist can be presented as follows:

Definition 4. The stable multistep method with the maximum degree pmax = k + 2 called as symmetric if the following take place: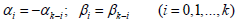

Let us noted that there are other definitions for symmetric methods given by the different authors. Among them, the best (in terms of application) is the definition given by Dahlquist. And now let us to consider the case k = 2 . As is known in this case the stable method with the maximum degree can be written as the follows:

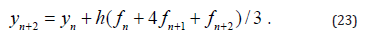
This method called as the Simpson’s method with the degree p = 4 . Noted that this method is symmetric according to Dahlquist’s laws. It is obvious that this Simpsons method is symmetric in relation to point of xn+1. Noted that methods Trapezoidal and Simpson have the maximum degree. And degree for these methods gets maximum value, namely pmax = 2k ( k =1 for and k = 2 ). Some authors take the midpoint rool, as the expleast symmetric method which is stable and has the degree max p = k . As is known if method (2) is stable in the case 0 βk = 0, then p ≤ k holds. Noted that there are methods, which scientists and specialists have taken as symmetrical. For example the following midpoint method:

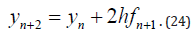
The coefficients of this method are satisfies of the Dahlquist law for the symmetrical methods. But the relation between of the order k and the degree of p suggested by Dahlquist is not satisfies. Noted that by using other Dahlquist result for the maximal value of the explicit methods, receive that the degree of method (24) has the maximum value pmax = k , so that it is explicit. Thus receive that the method (24), also has the maximum degree. And the local trancation error of the method (24) has an expansion in odd power begins from 3 (three). Therefore, by using Richardson’s extrapolitions or some similar method, one can increase the exactness of the values calculating by the named methods, considering the expantion of the local trancation error of the method (24). Noted that the coefficients of the method (24) satisfy the properties of Gauss quadrature methods. Thus have shown that the symmetric methods are more interesting that the others. And now let us consider the constraction of symmetrical methods and define some advantages of these methods. As is known, in solving some problems by using the numerical methods get some values, but to determine its reliability presents some difficulties. Some scientists for this propose to use the predictor-corrector methods, Richardson ekstrapolition, bilateral methods and others. For solving the named problem, here proposed to use symmetrical method, which can be defined as:

Definition 5. The multistep methods are called symmetrical if the exact values of the solution of considering problem to be located between of the values calculated by these methods.

To illustrate the benefits of symmetric methods, let us consider the following Euler’s methods:

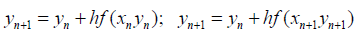
One of which is explicit and the other is implicit. As is known the local traction error for the Euler’s method can be presented as follows:

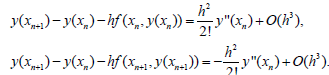
It is not hard to define that the exact values of the solution at the mesh point n 1 x + will be located between of the values calculated by the Euler’s methods. By using these properties of the Euler’s methods one can be constructed more exact methods. For example, by using these methods one can construct the trapezoidal rule. As was noted above the midpoint rule has some advantages, that can be prezented as one step and also as the two step method as following:

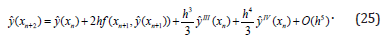
This method is explicit, and its degree receive the maximum value max p = 2 . As was noted above, method of (23) satisfies the condition of symmetric method given by Dahlquist. And now to consider the following method:

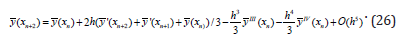
Noted that the methods (25) and (26) has the degree p = 2 . But the method constructed by using the following linear combination of these methods y(x) = ( yˆ(x) + y(x)) / 2 will has the degree p = 4 . In the result of this operation receive the known Simpson’s method having the following form.

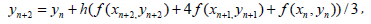
here has used the equality of y '(x) = f (x, y) .

Let us noted that the methods by which have constructed Simpson’s method were stable. But now let us consider construction methods with high accuracy by using predictor and corrector methods of the bilateral types.

For this aim let us consider to following predictor and corrector methods:

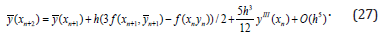
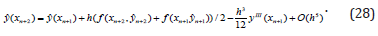
It is not difficult to understand that if calculate the value yn+2 by the linear combination 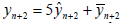, then receive that the value yn+2 more exact, than the values 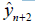and 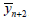, so as the method for calculation of the value yn+2, can be presented in the following form:

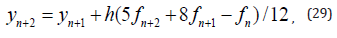
which is stable and has the degree p = 3 .

Let us note that the local trancation error for the method (28) has written at the mesh point xn+1, but for the method (27) the local trancation error has written at the mesh point n x . Therefor method (29) constructed by using (27) and (28) has the degree p = 3 . It is known that in the case k = 2 , method with the maximum degree is the Simpson’s method. Thus, have proven that by using the local trancation error, one can be conctructed more accurate methods. In this case arises the natural question about that by using above discriped way, how much can the accuracy of the method be increased? To determine this let us to consider the following prezentation of the local trancation error of multistep methods:

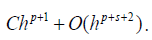
In the work [40] have proven that if the considering method is stable, then p + s ≤ 2[k / 2]+ 2 . But by using some schemes, one can increase the accuracy of the calculated values of the solution of the considering problem (see for example [40]). Noted that in this case the accuracy of the method is not increases. Increases only the accuracy of the calculating values of the solution considering problem. Thus, have proven that the using symmetrical or bilateral methods in solving applied problems is desirable. Let us note that the bilateral formula and the bilateral methods are different concepts. For example, let us to consider Euler’s methods, which can present as following:

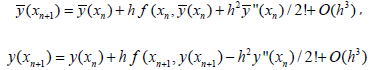
These formulas can be taken as bilateral formulas. For the bilateral methods the following should take place:

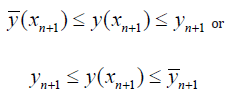
It follows that the construction of bilateral methods requires a special approach (see [41]).

For illustration of the results receiving here, in the following section have applied some of methods constructed here to solve model problem.

Numerical Results

Here, have considered to comparison of some multistep methods and for the define of advantages of these methods have used the conception of stability and degree for the multistep methods of advanced and hybrid types. And also, have shown the advantages of the bilateral methods and also of the advantages of the symmetrical methods.

Let us consider to solving of the following example:

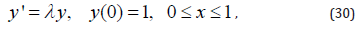
the exact solution for which can be presented by the function: y(x) = exp(λ x) .

To solve the problem (30), here have used the methods (16) and (21). The receiving results by using these methods for the values λ = ±1,± 5,±10 and for the h = 0.1; 0.2; 0.05 have tabulated in the Table 1- Table 6.

Table 1: Results receiving by the method (16) for the h = 0.05 .

Note*: By using the tabulated here results, receive that, the results, which have received for the values λ = −1 and λ = −5 can be taking as the better.

Noted that method (16) has degree p = 4, but the method of (21) has the degree p = 8 . By considering this information about of these methods in solving of the example began to increase the value of λ . For the values λ > 0 the solution of the example is increases, but for the values λ < 0 the solution of this example if decreases. Therefor in using of more exact method the step-size have increased, but for the method with low precision vice versa, the value of step-size has decreased. And now let us consider to application the method of (16) to solve example (30) and tabulated that in the following tables (Tables 1-6).

Table 2: Results receiving by the method (16) for the λ = ±10 .

Note*: It is not difficult by using above-described results that results receiving for λ = −5 and λ = −10 are better.

Table 3: Results receiving by the method (16) for the h = 0.1 .

Note*: According to the results of table 3, receive that getting results on negative λ is always the best.

Table 4: Results receiving by the method (21) for the h = 0.1 .

Table 5: Results receiving by the method (21) for the h = 0.2 .

Table 6: Results receiving by the method (21) for the λ = ±10 .

It is not difficult to define that from the results tabulated in Tables 4-6 it follows that results receiving on negative λ are the best. Here have compared some results using an unconventional way. To increase the accuracy of the calculated values, wanted to use halfsum of these values. In some cases, get a better result, but in general did not get o good results. As is known, if use a symmetrical methods, then get the best results according to the specified scheme. For example for the Euler’s methods, which can be represented in the following form:

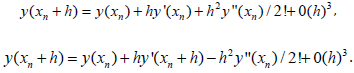
It can be easily shown that by the help of these symmetric methods it is possible constructed a bilateral methods. Noted that for this aim, here can be recommending the following hybrid methods:

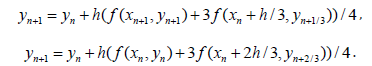
These methods usually give the best results [42-51].

Conclusion

Here, have described some of the results obtained in the field of stability of Multistep Methods. And also, tried to give on objective correction in development of the on the conception of “stability” for multistep methods with constant coefficients. It is not hard to understand that to describe the development of the numerical methods intended to solve of the initial value problem for ODEs and by comparison the results receiving the maximum value of accuracy of some numerical stable methods to define their advantages and disadvantages is not easy. Noted that by the construction of the concrete stable hybrid methods with degree p = 8 for k = 2 , prove existence of the stable hybrid methods of type (17) with the degree p = 2k + 2 . But by the construction of method (29) have shown the existence stable hybrid methods with the degree p = 3k + 3 . There are many works devoted to the investigation of hybrid methods. Here have investigated the linear hybrid methods more general form, therefore, has considered to finding the coefficients of the investigated hybrid methods. To determine reliable values of the solution of the investigated problem, here offer to use the symmetric or bilateral methods. For this aim has described the construction of bilateral methods and to increase the accuracy of the values of the solution investigated problem, which has calculated by using bilateral symmetric methods. Noted that the construction of bilateral methods is needed to define the local trancaton error and determinate of the signs of the coefficients k β for implicit and βk, βk+1,... for the advanced (forward-jumping) methods (see for example [22]).

Acknowledgments

The authors wishes to express their thanks to academicians Telman Aliyev and Ali Abbasov for their suggestion to investigate the computational aspects of our problem and for their frequent valuable suggestion. This work was supported by the Azerbai Science Foundation Grant No AEF-MCG- 2022-1(42)-12/10/4-M-10 (for Vagif Ibrahimov). The authors wish also to thank the anonymous reviewers for their careful reading of the manuscript and their fruitful comments and suggestions.

Conflict of Interest

There is no conflict of interest in this work.

References

• Volterra V, Theory of Functionals and of integral and integra-differential equations. Dover publications pp. 304.
• Voter V (1976) Mathematical theory struggle for existence M. Naka pp. 288.
• Polish Chuk EM, Volterra V, L Naka (1977) pp. 113.
• Murray JD (1977) Lectures on nonlinear differential equation models in biology, Clarendon press. Oxford pp.401.
• M Ivanova, V Ibrahimov (2023) The application of Hybrid methods to solve some problems of mathematical biology, American journal of Biomedical Science and Research pp. 793-799.
• Gupta G K (1979) A polynomial representation of hybrid methods for solving ODEs. Mathematics of comp 33(148): 1251-1256.
• Mamedov Ya D (1974) Approximate methods for solving ODE. Baku pp. 175.
• G Yu Mehdiyev, V Ibrahimov, M Ivanova (2013) On Research of Hybrid Methods. Numerical Analysis and Its Applications. Numerical Analysis and Its Applications Springer pp. 395-402.
• Verzhibitskiy VM (2001) Numerical methods graduate school. Moscow pp. 382.
• Galina Mehdiyev, Vagif Ibrahimov, Mehriban Ivanova (2014, 2016) General theory of the application of multistep methods to calculation of the energy of signals, Wireless Communications. Networking and Applications: Proceedings of WCNA pp.1047-1056.
• Atkinson K E (1997) Numerical solution of integral equations of the second kind. Cambridge University Press pp. 552.
• G Yu Mehdiyev, V Ibrahimov, M Ivanova (2012) Application of the hybrid method with constant coefficients to solving the integra-differential equations of first order. AIP Conference Proceedings pp. 506-510.
• Burden R, Douglas F (2001) Numerical analysis. Cengage Learning pp. 850.
• Butcher IC (2008) Numerical methods for ODEs. John Wiley@Sons, Ltd 463 p.
• G Yu Mehdiyev, V Ibrahimov, M Ivanova (2012) On the construction test equations and its Applying to solving Volterra integral equation, Mathematical methods for information science and economics. Montreux pp.109-114.
• Godunov SK, Rabbinic (1962) Introduction to the theory of difference Schemes. Moscow, Femmages.
• Shura Bura M R (1952) Error estimates for numerical integration of ordinary differential equations, Pirkle. Mate and mech 5: 575-588.
• Mukhin IS (1952) By the accumulation of errors in the numerical integration of differential-differential equations. Primate and mech 6: 752-756.
• Bacalao NS (1955) Some remarks on the question of numerical integration of differential equation by the finite-difference method. Academy of Science report USSA N3 pp. 805-808.
• MN Ivanova (2006) One the multistep method of numerical solution for Volterra integral equation. Trans Natl Accad Sci Azeeb Ser Phys Tech Math pp.95-104.
• Ahlquist G (1956) Convergence and stability in the numerical integration of ordinary differential equations. Math Scand 4: 33-53.
• Henrici P (1962) Discrete variable methods in ODG. John Wiley and Sons Inc.
• G Mehdiyev, V Ibrahimov, M Ivanova (2012) On one application of hybrid methods for solving Volterra integral equations. World Academy of Science, Engineering.
• Ibrahimov VR (1984) Convergence of the predictor-corrector methods. Applied Mathematics NRB Sofia pp.187-197.
• Ahlquist G (1959) Stability and error bounds in the numerical integration of ODEs, 85s. Stockholm. Tenaska Forskolin’s Handlanger 130: 195-987.
• Kobza J (1975) Second derivative methods of Adams type. Appliance Mathematic Ky 20: 389-405.
• Ibrahimov VR (1990) On a relation between degree and order for the stable advanced formula. Journal computational mathematics and mathematical Physics 7:1045-1056.
• Mehdiyev G Yu, Ivanova MN, Ibrahimov VR (2012) An application of the hybrid methods to the numerical solution of ordinary differential equations of second order. Vatnik Kanu, ser math mech 4(75): 46-54.
• Butcher JC (1965) A modified multistep method for the numerical integration of ordinary differential equations. J Assoc Compute Math 12: 124-135.
• G Mehdiyev, M Ivanova, V Ibrahimov (2016) An Application of Mathematical Methods for Solving of Scientific Problems. British Journal of Applied Science & Technology 1-15.
• Gear C (1965) Hybrid methods for initial value problems in ordinary differential equations, SIAM. I Number Anal 2: 69-86.
• Heggie IO, Okumura SA, Socolow AB, Yakupov MA (2010) On generalized 2-step continuous linear multistep, method of hybrid type for the integration of second order ODEs. Archives of Applied Research 2(6): 362-372.
• Ibrahimov VR, Ivanova MN (2021) On construction of multistep methods of the hybrid types and their application to solve integral equation with variable boundaries. Symmetry 13: 1087.
• Ibrahimov VR, Mehdiyev G Yu, Xiao Guang Xue, Mohammed Akbar, Samad Neasham, et al. (2021) Novel symmetric numerical methods for solving symmetric mathematical problems. International journal of Circuits, system and signal processing 15: 1545-1557.
• G Mehdiyev, M Ivanova, VR Ibrahimov (2008) On an application of the finite-difference method, News BSU (2): 73-78.
• (2012) Simos TE Optimizing a hybrid two-step method for the numerical solution of the Schrödinger equation and related problems with respect to phase-lag. J Appl Math pp.17.
• Simos TE, Tessituras C (2018) Fitted modifications of classical Runge-Kuttab pairs of orders 5(4). Math Meth Appl Sci 41: 4549-4559.
• Anastasi ZA, Simos TE (2005) An optimized Runge-Kuttab method for the solution of orbital problems. Journal of Computational and Applied Mathematics 175(1): 1-9.
• Ibrahimov, G Mehdiyev, M Ivanova (2022) On The Construction of Symmetrical Methods and Step by Step Method for Their Application to Solving Initial-Value Problem for ODEs. Proceedings of International Conference on Engineering, Science and Technology, 13-16 out 59.
• Abdulghani RI, Akinfenwa OA, Okumura AA (2017) Simpson type trigonometrically fitted block scheme for numerical integration of oscillatory problems. UJMST 5: 25-36.
• Ibrahimov, G Mehdiyev, M Ivanova (2022) Construction of Some Algorithm for Calculation of Definite Integrals by Using Advanced and Hybrid Methods. Proceedings of International Conference on Engineering, Science and Technology, 13-16 out 84.
• Ridwan Lahi Inyanda Abdulghani, Shipping Wen, Yuling Feng, Ning Tang (2021) Adapted block hybrid method for the numerical solution of Duffing equation and related problems. BIMS mathematics 6(12): 14013-14034.
• Tie Fang, Chonglin Liu, Chah-Wen Hsu (2019) Theodore Simos, Charalambous Tessituras, Explicit hybrid six-step, six order, fully symmetric methods for solving. Mathematical Methods in the applied Sciences 1-10.
• Monona’s Th, Calorizator Z, Hagino Rams, Simos TE (2015) A new approach on the construction of trigonometrically fitted two step hybrid methods. Proceedings of Intern. Conf on Numerical Analysis and Applied Mathematics, AIP Conf Proc 1648: 810009-1-810009-6.
• Mehdiyev G, Ibrahimov V, Ivanova V (2015) General theory of the application of multistep methods to calculation of the energy of signals. Lecture Notes in Electrical Engineering 348: 1047-1056.
• VR Ibrahimov, MN Ivanova, The New Way to Solve Physical Problems Described by Ode Of The Second Order With The Special Structure. Seas Transactions on Systems.
• Ernst Hairier (2006) Symmetric linear multistep methods. Numerical Mathematics 46: 515-524.
• Hairier E, Lubick C (2004) Symmetric multistep methods over long times, Number. math pp.97699-723.
• Ibrahimov VR (1990) On some properties of Richardson’s extrapolation, Infeudations. USSR 12: 2170-2173.
• Quinlan GD, Tremaine S (1990) Symmetric multistep methods for the numerical integration of planetary orbits. Astronomy 100: 1694-1700.
• Ibrahimov VR (1984) About a way to construct bilateral methods. Applied mathematics pp.199-207.