DFT Study About Adsorption of a C₁₄ Carbon Ring on An Organochlorinated DDE Compound

The aim in this case is to get a DFT study on the interaction between a C₁₄ activated carbon ring and an organochlorinated DDE (Dichlorodiphenyldichloroethylene) compound for its possible adsorption, in order to increase DDE compound. The latter is a metabolite of DDT (Dichlorodiphenyltrichloroethane) pesticide, with negative environmental effects causing diseases in human beings. DDE as DDT degradation loses its insecticidal action but is still harmful to health accumulating it in the fatty tissue of living organisms such as humans. In view of this, the World Health Organization (WHO) classified it as a persistent organochlorine compound based on the danger or degree of toxicity from one or multiple exposures in a relatively short period of time [1]. Consequently, it is necessary to analyze alternative models allowing to remove this pollutant to minimize its effect.

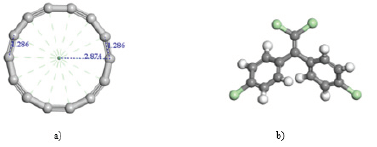
DDE (Dichlorodiphenyldichloroethylene) C₁₄H8C4, is a product of degradation of the DDT [2], and the most important chlorinated hydrocarbon insecticide ever marketed, was widely and extensively used in the 1940`s and 1950`s to control insects for protection of both agriculture and human health. It is the most stable metabolite of the organochlorine insecticide and has been identified as having estrogenic activity [3]. For removal of DDE, an economical and simple method is adsorption [4]. Adsorption is a process in which the atoms on a solid surface, attract and retain molecules from other compounds [5]. It is necessary to make contributions to help the search of materials improvement to reduce this toxic compound [6]. This research has focused in the interaction between carbyne type (-C≡C-…-C≡C-) C₁₄ ring structure, and DDE (2, 2 - bis (p - clorofenil) - 1, 1 – dicloroetileno), (Figure 1), showing characteristics allowing adsorption phenomenon to appear.

Figure 1: a) Rings C₁₄ actived carbon b). DDE

One of the carbon properties is that with atoms of the same element, it is possible to give place to different allotropic forms of car- bon materials: graphite, graphene, diamond, nanotubes, fullerenes, nanofoam and carbyne type rings by to mention some [7]. They are differentiated by the way in which the carbon atoms are structurally arranged, hence the chemical, physical and mechanical properties of each material arise. For this reason, both theoretical and experimental, a variety of studies have been carried out on how carbon structure geometry impacts in the properties of each material [8]. The adsorption as carbon property, is a process by which the atoms on a solid surface, attract and retain molecules of other compounds. These attraction forces are known as “Van Der Waals” forces (physisorption) [9]. Therefore, given that this is a phenomenon occurring on the surface, the greater the surface area available on a solid, the better adsorbent can be

On the interaction of DDE molecule with C₁₄ carbon ring, reactivity properties of each one of them were estimated: chemical potential, chemical hardness and electrophilic index, considering the molecular orbitales HOMO and LUMO for the adsorption analysis by applying geometry optimization [1 ],11]. In addition, the GAP is also calculated using HOMO-LUMO energies [12]. Geometry optimization is an iterative procedure that tries to locate a minimum of energy by varying lengths and angles up to equilibrium state where the molecular structures are stable [13]. When atoms and molecules approach each other, intermolecular forces begin to emerge. At very short distances these are repulsion forces; however, as the separation increases, they change to be of attraction. These forces generate a well of asymmetric potential similar to that of Lennard- Jones, which shows the position of the minimum potential energy, indicating equilibrium distance and bond force magnitude of the potential well [14].

To calculate reactivity indexes by means of the formulas proposed by Koopmans [15], the HOMO and LUMO energies of each C₁₄ and DDE molecules have been obtained. HOMO (the highest occupied molecular orbital), is the occupied OM of greater energy and the first empty molecular orbital is the LUMO (the lowest unoccupied molecular orbital) which is of lower energy. The reactivity between two molecules increases according to the extent that the HOMO of one of them and the LUMO of the other are closer [16].

In the Density Functional Theory (DFT), the energy can be expressed in terms of electrons number N, and the external potential V, which provides a series of mathematical expressions that form a set of global and local quantities that allow to quantify the reactivity concept [17]. To study reactivity indexes of molecules, the following descriptors are calculated: Chemical potential μ which measures the tendency of electrons to escape from the electronic cloud, chemical hardness η global ownership of the system that measures the resistance imposed by this to the change of its electronic distribution [18]. Similarly, the electronegativity χ is calculated, a property that measures tendency of electrons to remain in balance system [19].

Fukui indexes are local reactivity indexes giving us information on the atoms of the molecule that have a greater tendency to lose or accept an electron, those who are more likely to suffer a nucleophilicity or electrophilicity attack [20]. These indexes represent the sensitivity of the chemical potential μ due to the change of electronic density when the number of electrons changes [21]. The electrophilicity ω is associated with the energy of the lowest unoccupied molecular orbital (LUMO) and measures reactivity towards a donor reagent. The nucleophilicity N is associated with the highest energy molecular orbital (HOMO) and measures reactivity towards an acceptor receptor [22]. The electrophilicity ω scale allowed the classification of organic molecules as strong electrophiles with ω>1.5 eV, moderate electrophiles with 0.8 <ω<1.5 eV and marginal electrophiles with ω < 0.8 eV [23].

Electronic density and electrostatic potential are important aspects in the reactivity, as shown on C₁₄ and DDE molecules as these are generated by DMol3 software, respectively; becoming in a useful application to predict reactivity of molecules on each point of the space. It allows to visualize the regions of the space towards which particles are attracted either positively or negatively (regions of either positive or negative electrostatic potential) [24].

In the analysis of the ground state for electronic structures on model systems, a variational procedure is used; in which the functional of the electronic energy is minimized with respect to the electronic density by means of Density Functional Theory DFT [25] on Dmol3 developed by Delley [26], who used to achieve modeling and geometry optimizations, and the calculation of equilibrium distances and dissociation energy. For all electron calculations, a correlation functional proposed by Perdew-Wang in 1991 [27] using Generalized Gradient Approximations (GGA-PW91 level of theory), non-restricted spin, self-consistent field (SFC) with DND basis functions equivalent to 6-31G* basis [28].

The reactivity indexes for a system of N-electrons with total energy E and external potential V(r) are defined as the first and second derivative of E regarding N with the following expressions [29]:

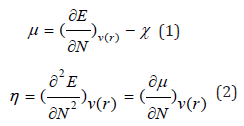
The equations 1 and 2, for μ and η respectively, are numerically determined by approximations based on finite differences of three points, as shown in the following expressions 3 and 4 [30], using the energies E_LUMO and E_HOMO for GAP (ELUMO - EHOMO) calculation [31]. The softness S is the inverse of η chemical hardness, and constitutes a useful concept on the prediction of chemical reactivity [32], as shown in the following expressions:

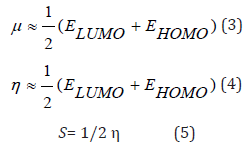
The electrophilicity index [33] is calculated by the expression:

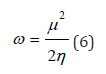
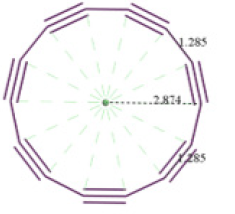
It is modeled a closed structure of 14 carbon atoms, to which a geometry optimization is carried out. This allowed to obtain a uniform ring type of 14 carbon atoms with alternating single- and triple-bonds, and bond length of 1.285 Å, as shown in (Figure 2), also with an approximate radius of 2.874 Å, a binding energy of -3830.310 kcal/mol, approximate perimeter of 18.027±0.023 Å, and an area of 25.949Å^2.

Figure 2: C₁₄ carbon atoms ring structure.

Table 1: Reactivity parameters the C₁₄.

Figure 3: HOMO-LUMO C₁₄.

In (Figure 3), it is represented the molecular orbital borders HOMO and LUMO of structure showing blue lobes positive and yellows lobes negative. Energies EHOMO and ELUMO of each structure, as well as the energy difference between HOMO and LUMO (or energy GAP), are shown in (Table 1). A large GAP energy difference corresponding to stable and low reactive systems (> 5eV ) is considered insulating, while with a small difference (< 0.5eV ) hopefully the system is not stable and highly reactive, and it is considered as conductor. In this structure the value is 2.759eV ,then it can be considered as a semiconductor [27] as in (Table 1) where the whole parameters are shown.

Figure 4: Electronic density and electrostatic potential.

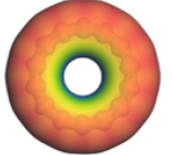
The electrostatic potential maps on (Figure 4) allow to visualize how electrons are distributed in carbyne molecules, the red color indicates regions where electronic density is higher, while blue regions indicate lower electronic population. The intermediate states follow the order of the rainbow from the center up to the external border, according to a greater or lower presence of electrons, and thus the green and yellow colors close to the center border of the structure indicate a homogeneous electronic balance. Carbon atoms only possessing the same electronegativity should give an almost homogeneous electronic distribution, and there is no preferential place where electrons be circulating, but our map tells us that the external part of carbyne structure has major electronic density.

Figure 5: a) 80-81-HOMO-LUMO (dot mode), b) 80-81-HOMO-LUMO c) Electrostatic Potential.

Table 2: Reactivity parameters of C₁₄ H8 Cl4.

Likewise, the HOMO and LUMO energies of DDE are calculated as shown in (Figure 5) indicating the zones of greater reactivity. HOMO energy -4.445 eV and LUMO energy -4.363 eV (Table 2).

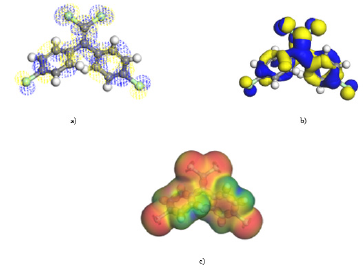
With the active zones of each analyzed structure, a reference is given about in which way DDE is accommodated, and the carbon structure can be put it in a mode, that may be estimated in a sustained way that some type of adsorption exists between the two molecules. (Figure 6) shows the way in which the carbon structure with a DDE molecule is placed, and (Figure 6b) exhibits the final state of minimum energy, after achieving geometry optimization by means of SCF calculations.

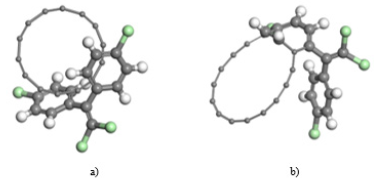
Figure 6: a) Initial structure of carbon and DDE molecules, b) Final structure after SCF geometry optimization.

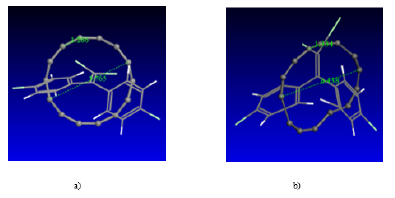
Figure 7: a) Initial structure of carbon and DDE molecules, b) Final structure after geometry optimization.

Interactions are also made by placing the DDE inside the carbyne ring as shown in (Figure 7). Geometry optimization is obtained and what observed is that only the carbyne ring is deformed.

Using molecular modeling with DFT methodology in this work, it was observed adsorption capacity of C₁₄ activated carbon, which is to depend on the orientation to be placed with respect to DDE molecules. When the HOMO and LUMO of these molecules are overlapped in some region, adsorption is achieved. With the map of the electrostatic potential it could be observed that in the structure of the carbyne, the part having more electronic density is the external part, hence when placing the DDE molecule inside of the ring there was no adsorption phenomenon, only a deformed ring. The part with the most electronic DDE density is where the hydrogens are, then we put them outside the ring and DDE is added into the external part of the carbon structure.

For the prediction of reactivity, it is important to know the reactive sites of the molecular system to visualize specific parts where the adsorption phenomenon was given. DFT as a quantum theory based on electronic density, was useful in calculating the reactivity indexes to justify why and how the interactions among the molecules C₁₄ and C₁₄H₈C_l4 occur. The chemical potential μ calculated in each molecule shows us the tendency of electrons escaping from a system in equilibrium, so that the electrons flow from the regions of high chemical potential towards regions of low potential , μ_(C₁₄ )=-4.816 eV and μ_(C₁₄H₈C_l4)=-3.554eV, which tells us that there is a low and high potential, thus there would be the possibility of a molecule yielding or accepting electrons respectively. With regard to the resistance to modify the electronic distribution of each molecule, called η hardness, the following values were obtained η_(C₁₄ )=1.379 eV and η_(C₁₄H₈C_l4)= 1.809eV, which indicates that the DDE is more stable than the C₁₄, the electrophilicity ω tells us when the system is subjected to a electrophilic attack, where the electrons involved come from the HOMO. The values of ω_ (C₁₄) =8.4 eV and ω_(C₁₄H₈C_l4) = 3.464 eV show that they are strong electrophilic, since they are in the range of ω>1.5 eV, stressing that C₁₄ have the highest value, and it is more likely to attract electrons. The electrophilicity ω is related with electronic affinity as they both measure the ability to accept electrons, but the electrophilicity ω measures the energy decrease due to the maximum electron flow between donor and acceptor. These intrinsic properties of the molecules indicate the availability that an adsorption may exist. The adsorption allows a new molecule to be formed, so that the DDE (C₁₄H₈C_l4) grows to C28H8Cl4 upon adsorption of the C₁₄ carbon ring. This growth helps the human beings to eliminate it, since otherwise it can go to be stored in the fatty tissue with possible consequences to some disease.

• Yáñez L, OrtizPérez D, Batres LE, Borja-Aburto VH, Díaz-Barriga F (2002) Levels of dichlorodiphenyltrichloroethane and deltamethrin in humans and environmental samples in malarious areas of Mexico. Environ Res 88(3): 174-181.
• L Shen, F Wania (2005) Compilation, evaluation, and selection of physical-chemical property data for organochlorine pesticides. J Chem Eng Data 50(3): 742-768.
• J Kim, Q Sun, Y Yue, K Sup Yoon, KY Whang, et al. (2016) 4,4′-Dichlorodiphenyltrichloroethane (DDT) and 4,4′-dichlorodiphenyldichloroethylene (DDE) promote adipogenesis in 3T3-L1 adipocyte cell culture. Pesticide Biochemistry and Physiology 131: 40-45.
• JL Figueiredo, MFR Pereira, MMA Freitas, JJM Órfão (1999) Modification of the surface chemistry of activated carbons, Carbon 37(9): 1379-1389.
• D Duff, S Ross, D Vaughan (1988) Adsorption from solution. An experiment to illustrate the Langmuir adsorption isotherm. Journal of Chemical Education 65(9): 815-816.
• Battu RS, Singh PP, Joia BS, Karla RL (1989) Contamination of stored food and feed commodities from use of HCH and DDT inmalaria control. Sci Total Environ 78: 173-178.
• X Bourrat (1998) Design and control of structure of advanced carbon materials for enhanced performance, Kluwer Academic Publishers, Netherlands, p. 43-64.
• Lillo MAdlC (1999) Fibras de carbón y carbones activado: Caracterización y aplicaciones en separación y almacenamiento de gases in Química Inorgánica, Universidad de Alicante, Alicante, pp. 232.
• Peter W Atkins, Ronald S Friedman (2005) Molecular Quantum Mechanics. (4th edn), Oxford University Press, p. 72-80.
• JC Kotz, P Treichel, GC Weaver (2006) Chemistry & Chemical Reactivity. 6th Edition,408.
• J Wiley, Sons (1976) Fleming Frontier Orbitals and Organic Chemical Reactions.
• TM Krygowski (1993) Crystallographic studies of inter- and intramolecular interactions reflected in aromatic character of pi.- electron systems. J Chem Inf Comput Sci 33(1): 70-78.
• HB Schlegel (1982) Optimization of Equilibrium Geometries and Transition Structures. Adv Chem Phys 67: 249.
• JP Hansen, L Verlet (1969) Phase Transition of the Lennard-Jones System. L Phys Rev V184 N1.
• J Moncada, G Morán (2008) Quim Nova, 31:1255.
• RG Pearson (1986) Ionization potentials and electron affinities in aqueous solution. J Am Chem Soc 108(20): 6109-6114.
• RG Parr, Y Weitao (1989) Density-Funtional Theory of Atoms and Molecules. Oxford University Press, UK.
• Robert G Parr, László v Szentpály, Shubin Liu (1999) Electrophilicity Index. J Am Chem Soc 121(9): 1922-1924.
• RG Parr, RG Pearson (1983) Absolute Hardness: Companion Parameter to Absolute Electronegativity, Journal of the American Chemical Society, 105(26): 7512-7516.
• Fukui K (1982) The Role of Frontier Orbitals in Chemical Reactions. Angew Chem Int Ed Engl 21(11): 801-876.
• P Pérez, LR Domingo, A Aizman, R Contreras (2009) The Electrophilicity Index in Organic Chemistry.In Theoretical Aspects of Chemical19: 139- 201.
• Robert G Parr, László v bSzentpály, Shubin Liu (1999) Electrophilicity Index. J Am Chem Soc 121(9): 1922-1924.
• Domingo LR, Aurell MJ, Pérez P, Contreras R (2002) Quantitative characterization of the global electrophilicity power of common diene/ dienophile pairs in Diels-Alder reactions. Tetrahedron, 58: 4417-4423.
• Vivas Reyes, Ricardo, Zapata, Jhon (2008) Estudio teórico de la reactividad de las conformaciones y configuraciones de los ácidos grasos omega-3 a través de descriptores moleculares de reactividad utilizando la Teoría del Funcional de la Densidad (DFT). Rev Colomb Quim 37(2): 145-160.
• Sierralta A, Lisboa O, Rodriguez L (2005) Density functional theory calculation for H4citation_volume dissociation on MoS2 and NiMoS cluster models. J Mol Structure 729: 91-97.
• B Delley (1990) An all‐electron numerical method for solving the local density functional for polyatomic molecules. J Chem Phys 92: 508.
• John P Perdew, Kieron Burke, Matthias Ernzerhof (1997) Generalized Gradient Approximation Made Simple. Phys Rev Lett 77: 1396.
• J Baker, A Kessi, B Delley (1996) The Generation and Use of Internal Coordinates in Geometry Optimization. J Chem Phys 105(1): 192-212.
• Maynard AT, Huang M, Rice WG, Covell DG (1998) Reactivity of the HIV- 1 nucleocapsid protein p7 zinc finger domains from the perspective of density-functional theory. Proc Natl Acad Sci 95(20): 11578-11583.
• JI Martinez Araya, D Salgado Moran, J Glossman (2013) Computational Nanochemistry Report on the Oxicams Conceptual DFT and Chemical Reactivity. Chem 1: 9.
• RG Parr, RA Donnelly, M Levy, E Palke (1978) Electronegativity: The density functional viewpoint. The Journal of Chemical Physics 68: 3801.
• PW Ayers, RG Parr (2000) Variational Principles for Describing Chemical Reactions: The Fukui Function and Chemical Hardness Revisited. J Am Chem Soc 122(9): 2010- 2018.
• JL Gazquez, Andres Cedillo, Alberto Vela (2007) Electrodonating and electroaccepting powers. J Phys Chem A 111(10): 1966-1970.