Computational Cybernetics of Epidemic Disease Propagation: Vertical Transmission and Attraction Domain Dynamics*

Introduction

Innovated developments of bio-medical cybernetics [1-3] as systems biology science, that is, as an intersection of systems science and of mathematical biology [4], have been successfully extended to the study of various phenomena in human communities including the spread dynamics of epidemic diseases propagation. Literature [5-7] showed that rather useful algorithmic systemic models and simulation results have been obtained that have shed a novel insight and more axiomatic rather than hypothesis knowledge in systems biology. Thus, exploring the epidemics/pandemics phenomenal constitute very important research not area only in life sciences of biology and medicine but also in mathematics, physics and bioengineering nowadays. Many reported research works, referenced in the article, have demonstrated systems biology should be considered hence understood as a rightful holistic intersection of methods of computational cybernetics and mathematical biology with systems and control sciences. In, studies of the spread dynamics in epidemic diseases propagation, their asymptotic behaviour and the feasibility of extinction and/or persistence via domain(s) of attraction (DoA) governing spread dynamics, with centrality issue of stability at their heart essence.

This review research and its previous results [8-10], are confined on classes of epidemic models susceptible-infectious-removed and susceptible-infectious-removed-susceptible (SIR and SIRS) first explored in [5,6,11,12]. For, public health issues are becoming more and more important in society [3,13]. Epidemics refer to a disease that spreads extensively and rapidly by infection and affecting many individuals in an area or a population at the same time. Some examples are the SARS in 2002 or the swine flu and more recently Covid-19 and other infection spreads [9,14].

Traditionally [15] mathematical modelling of the temporal evolution of an epidemics/pandemic make use of deterministic and stochastic differential equations [16,17]. However this approach has some serious drawbacks in that it neglects the local character of the spreading process, it does not include variable susceptibility of individuals, and cannot capture and handle notorious boundary and initial conditions, thus other mathematical and computational methods are needed as well. Cellular automata [18-21] can overcome these drawbacks and have been used by several researches as an efficient alternative method to study epidemics spread propagation. In particular, Wolfram [21] argued in the cellular automata (CA) were originally introduced by R. Ulam and J. von Neumann in 1950s with the aim to develop and establish models of biological self-reproduction [22]. Also, Wolfram [21] pointed out in soon F. Amoroso, R. Fredkin and J. Cooper have proposed a simpler replicator algorithm based on parity or modulo-two rules based on von Neumann’s ideas. Only then Wolfram developed his computation theory of cellular automata. On these grounds independently Fuentes and co-authors [18] in and Willox and co-authors [22] in developed further and established the axiomatic theory of the CA-modelling epidemic spread and its applications. In those studies, by relevant applications the CA were proven to represent simple and yet computational cybernetic model capable to emulate complex physical, biological or environmental phenomena. Nonetheless, first concept and notion of a cell had appeared in conjunction with the set-theoretic operation of set partition [20].

A much more difficult problem and delicate too appeared explorations in the dynamics of epidemic propagation and estimation of the domain-of-attraction [2]. Although these explorations on domain-of-attraction (DoA) are based on classes of SIR and SIRS epidemic models, the assumption of varying-size population and constant immigration is prerequisite. Furthermore, assumption that both the disease-free equilibrium and the endemic equilibrium do exist is also needed. These problems have been explored by appropriate techniques of computer simulations using the especially derived mathematical models and computing algorithms. In particular, the DoA of epidemic model dynamics was widely estimated by using sum-of-squares (SoS) optimization approach. This estimation study for SIRS epidemic models has been carried out by using sum-of-squares optimization methodology.

The actual computations were performed by employing the ‘SeDuMi’ semi-definite optimization platform due to Henrion and Lasserre [23]. The viability of all these ideas has been confirmed by the successful application to theoretical SIRS models. The obtained computer simulation results enabled the proposed optimization approaches for analysing SIR and SIRS epidemic models with respect to domain-of-attraction to be compared with results of more traditional Lyapunov [24] theory, based LMI approach. The respective advantages and disadvantages appear well revealed hence provide valuable information for analysing the diseases spread infection mechanisms, and thus possibly forecast the future trends of infectious diseases. It is believed that these findings can help to assess the effectiveness of prevention and treatment as well as of managing programs.

The estimation of domain of attraction (DoA) for large-scale interconnected systems [25], that is, region(s) in state space where system dynamics is asymptotically stable, have been explored by many researchers due to its importance in both theoretical studies and practical applications. For, it is an essential research topic for the stability analysis of hybrid and nonlinear systems as well as in optimization methods. The study of the DoA for the epidemic disease model is thus important since it can give guidance how to forecast or determine the developmental trend of epidemic infections and therefore adequate help to societies. The solution can be used to describe the spread characteristics of infectious diseases, predict the status of infection and evaluate the efficiency of the control strategies for infection spread.

Among more recent studies Brauer and Castillo-Chavez [4] applied stability analysis theory to find the equilibrium for the SIRS epidemic model. In their respective works, Li and Jin [26], Tang and Li [27], and Li and Ma [28], the global asymptotic stability of both disease-free equilibrium and a possible endemic equilibrium have been analyzed. The local stability analysis and optimal vaccination of a class SIR model was investigated in [29]. The local stability of the equilibrium for SIRS and SEIRS models had been considered in [30] under the assumption that the incidence rate was given. Hahn [31] has proved that the estimation of the domain of attraction for nonlinear dynamical systems based on Lyapunov stability theory [32] can be translated into an optimization problem and then solved using optimization methods [31]. Thus in order to analyze the epidemic model not only qualitatively but also quantitatively, many scholars paid special attention to certain optimization problems involved.

An optimization approach for finding the DoA of a class SIR models, based on the moment theory, is presented in [33]. Further, Matallana, et al. [34] computed the DOA in epidemiological models with constant removal rates of infected individuals. In addition, Makinde [35] has contributed a domain decomposition approach to a SIR epidemic model with constant vaccination strategy. A translation of the severely constrained optimization problems into Linear Matrix Inequality (LMI) problems based on the moment theory is given in Lassere [36,37]. This method has been linked with the choice of a Lyaponv function thus yielded a LF-LMI technique. In addition, Lassare [36] managed to expand the robust optimization approach into the hard polynomial programming problems. Also, Hachico and Tibken [38] gave an algorithm for solving the optimization problems for estimation of DoA via employing LMI techniques. It was further innovated by Hachico [39] in which he yielded expedient computational time thus important and valuable improvement.

The Sum-of-squares optimization method (SoS) [40-42,14] and [43-45,30] via employing the LMI technique to mathematical biology was introduced Chesi [40] and further extended in Chesi, et al. [41] and Chesi [14,42]. The power of the SoS method stems from the fact that SoS problems result in semi-definite programs (SDP), which are solved efficiently in polynomial system models. Furthermore, it was re-elaborated in considerable depth for the purpose of computing the polynomial Lyapunov functions for nonlinear systems in Jarvis-Wloszek’s [46] doctoral dissertation. In turn, many researchers exploited the SoS method to provide lower bounds on the largest estimation of the DoA using convex LMI optimization techniques. A certain new development of SoS optimization was given in Prajna, et al. [47]. Another analysis technique for the stability region with SoS programming was proposed by Tan and Packard [48]. The local stability analysis by combined usage of simulations and sum-of-squares programming was given in work by Topcu and Packard [49]. Novel developments of the SoS optimization in control applications have been given in [9,10] and in [8,13].

A natural follow up of these results is that the optimization problem of the DoA for a given class of systems has gained research interests among systems and control scientists, because it appeared a rather important problem in the field of mathematical and systems biology. Moreover, it appeared to include considerably involved issues of computational cybernetics in a systems control problem setting. This paper is one of those studies dedicated to the estimation of DoA for a class of three-dimensional SIRS epidemic model for varying-size population with constant immigration. Also, in the present setting, the death factor in the conditions, which was first exploited ny Lan, et al. [30], is included into consideration. In view of the problem complexity and the need for computational efficiency, a novel sum-of-squares optimization for analysing the epidemic model and estimating the DoA is proposed. It was shown that an invariant subset of domain of attraction can be successfully computed and even enlarged to its feasible probabilistic boundaries.

Further this paper is organized as follows. Section II reviews the preliminaries and the background knowledge on general SIRS epidemic model dynamics as well as analyzes the local stability of the given system dynamics. The methodological technique of using the CA approach in order to study the effect of the vertical transmission on the epidemic propagation is developed in sections III and IV. In the established model, individuals are assumed to be distributed in the cellular space such that each cell stands for an individual of the population it is aimed at. Three classes of population are studied and simulation results given: susceptible, infected and recovered. Further, the model also has been extended to include the effect of the vaccination of some parts of the population on epidemic propagation. Thus, it can serve as a basis for the development of algorithms to simulate real epidemics based on real data, which is subject of future research. In Section V, the novel estimation of the DoA for the SIRS epidemic model dynamics using SOS optimization algorithm is presented. In Section VI, a illustrative example and its numerical simulations are given to demonstrate the effectiveness and feasibility of the proposed method, and issues of domains of attraction for future research indicated. Concluding remarks are presented in Section VII.

On SIRS Theoretic Models and Preliminaries

Following X Mao [16] and works [19,50,30,36] a fairly general class of epidemic models is described by means of the following stochastic differential equation [37] with general nonlinear incidence coefficients:

Notice quantities and symbols in both (1) and (3) denote: variables S(t), I(t), R(t) represent number of death rates of susceptible, infectious, and removed at time t , respectively; A is the requirement rate of the total population, μ is the natural death rate, γ is the recovery rate of infected individuals, and α is the disease related death of infected individuals; δ is the rate of loosing immunity for removed individuals; f(S,I,R) and g(S,I,R) represent unknown nonlinear incidence events.

A Note on the Class of SIRS Epidemic Models

The following deterministic and simplified SIRS epidemic model can be derived from Eqs. (1a)

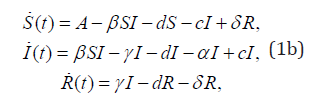
where quantity β represents the bilinear infection rate. Now, respectively, death rates of susceptible, infectious, and removed/recovered at time t represented as S(t), I(t), R(t) are the state variables of epidemic dynamics. Symbol α is the population input rate constant. Constants d and γ denote the coefficient of the natural recovery and mortality rates of the population. Quantity c denotes the susceptibility rate (not immune) and δ is the immunity loss ratio of the restoration people in units of time. Further, the size of total population at time t may be denoted by N, with N=S+I+R. In turn, it should be also noted that N’=A– N – I.

Suppose quantity R₀ = (β A)/(d(α +β + d + c)) describes the basic reproduction number, which determines whether the disease dies out or remains alive. Then the global asymptotic stability of the disease-free equilibrium and the endemic equilibrium implied by the SIRS epidemic model dynamics can be analyzed and established. Let denote P₁(A/d,0,0) the disease-free equilibrium and P₂(p₁,p₂,p₃) the endemic equilibrium where:

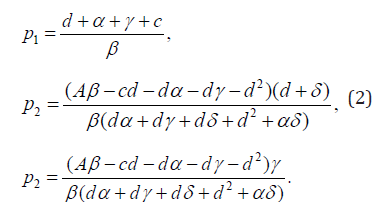
It is natural to assume the population numbers to tend to the constant A/d, and when N>A/d then it follows N'< 0 too. Thus, all solutions will either lie or tend in a regional area, which may be denoted as follows:

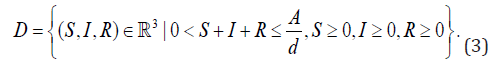
Lemma 1 [5]. If R₀ < 1, the unique equilibrium point of the SIRS model P (A / d, 0, 0) is globally asymptotically stable. If R₀ > 1 , the endemic equilibrium P₂(p₁,p₂,p₃) is locally asymptotically stable but P₁ is not stable.

Remark 1. When R₀ < 1, regardless of the initial number of patients, the disease will not develop and will gradually disappear in the group (the point P(A/d,0,0) is the disease-free equilibrium point). When R₀ >1, the disease will expand, and the stability number of the susceptible individuals and the illness individuals can be expressed, respectively, as follows:

In thus developed process of epidemic diseases the point P₂(p₁,p₂,p₃) is the endemic equilibrium point.

A Note On Sum-of-Squares Optimization Method

A multivariate polynomial p(x) = p(x₁ , x₂ ,..., x_n) is a sum of squares, if there exist polynomials f_i(x),i = 1,...,m such that

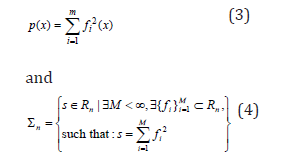
is the set of SoS in n variables. The existence of an SoS decomposition can be shown to be equivalent to the existence of a positive semi-definite matrix Q, such that:

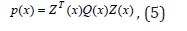
where Z(x) is the vector of monomials of degree less than or equal to deg(p)/2. The decomposition (3) can be easily converted into (4) and vice versa. This equivalence makes SoS decomposition computable using semi-definite programming, since finding a symmetric matrix Q subject to the affine constraint (4) is nothing but a solvable semi-definite programming problem. Sum-of-squares program is a convex optimization problem as follows:

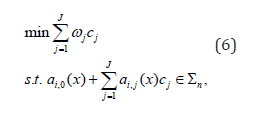
where c_j are scalar real-valued decision variables, ω_jare given real numbers, and a_i,j(x) are given polynomials (with fixed coefficients).

Remark 2. Some known SoS optimization problems can be solved using the computing toolbox SOSTOOLS [47], which is free, and by means of the MATLAB third-party toolbox the sum-of-squares programming tasks.

On Cellular Automata Theory

The cellular automata (CA) represent a category of finite state dynamical systems [20,51] in which space and time are represented by discrete finite sets (concept of cells emerged from set partition operation). The cells are arranged in the form of a regular set lattice structure and each must have a finite number of states. These states are updated synchronously according to a specified local rule of interaction. At each step, each cell computes its own new state from that of its close neighbours [32,52]. Thus, the laws of such a system are local and uniform. Though the CA, even starting from a complete disorder, their irreversible evolution is capable of spontaneously generating ordered structure. For example, a simple two-state, one-dimensional cellular automaton will consist of a line of cells, each of which can take either value 0 or 1. Using a local rule (usually deterministic), the values are updated synchronously in discrete time steps for all cells. With a K-state automaton, each cell can take any of the integer values between 0 and K −1. In general, the rule governing the evolution of the cell automaton will encompass m sites up to a finite distance raway. Such cellular automaton is called a K-state, m-site neighbourhood CA [21,22].

Similarly, as the one-dimensional CA, a two-dimensional cellular automaton consists of a uniform grid, with each grid taking on a finite set of possible values, which are updated in discrete time steps according to a deterministic rule involving a local neighbourhood of the grid around it. Let L be a regular set lattice (i.e. cells are the elements of L), with S is a finite set of states, s₀∈S, and s₀ is the initial state. Let N be a finite set (of size n = N ) of neighbourhood indices such that ∀r∈L , ∀c∈N such that r + c∈L, and let function f : Sn →S be state transition function. Then, the quintuplet C = {L,N,S,f,s} defines and is called a cellular automaton. An association configuration C_t:L→S of time t is a set function that associates a state with each cell of the lattice L . The role effect of the transition function f is to change the configuration of celullar automaton C_t at time t into the new configuration C_t+1 time t+1 according to the rule:

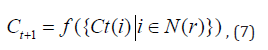
where N(r) denotes the set of neighbours of cell r,

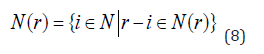
As the CA is needed in order to simulate a real-world process and search for solution to real-world problem, the next step is to conclude and define the crucial set-theoretic issues. Namely, the choice or construction of: the lattice geometry, neighbourhood size, boundary conditions, initial conditions, set of states, and the transition rule [21,22].

The lattice geometry consists of the lattice dimension and lattice shape. It is supposed the grounds where the epidemic is spreading stands for the cellular space of the CA, and it is partitioned into identical square areas, each representing one cell of the CA. Then neighbourhood in which cells can interact is matter of choice according to envisaged spread environment. The neighbourhood is usually described by specifying the set of cells that neighbour a given cell inside the CA.

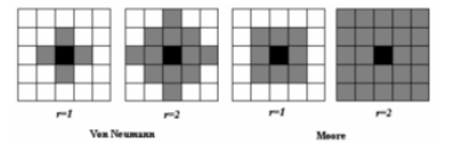
For a square lattice, two types of neighbourhood are typically used. The first choice is the generalized Von Neumann neighbourhood of radius r [22]:

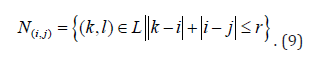
The second one is the Moore neighbourhood of radius[22]:. (10)

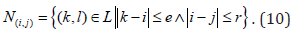
Both are depicted in Figure 1 for values of the radius r=1 and r=2 of the neighbourhood.

Figure 1: On definitions of the neighbourhood in cellular automata.

Constructing of Proposed Models and Computer Simulation Results

In this section, the mathematical model based on cellular automata for simulating the spread of an epidemic disease having the characteristic feature of vertical transmission. The individuals are assumed to be distributed within the cellular space such that each cell stands for an individual of the entire population.

Constructing of Cellular Automata Models

The cellular space is considered to be large enough to ensure that spreading of the epidemic affects only to the central region of the state process space. The Moore [52] neighbourhood and radius r=1 have been used in developing the CA-based model. The main features of the epidemic and the environment where it is spreading can be summarized as follows:

(i) The epidemic is not immigration or emigration, natural death and birth is considered, with b is birth rate and d is natural death rate.

(ii) The population distribution is inhomogeneous, the total population of the cellular space is M0 at the initial time t₀ , and the population at arbitrary time tis M₀

(iii) It is suppose that the way of infection is the contact between the infected individual and the healthy individual; the involved incidence rate is β.

(iv) We consider the characteristic of vertical transmission. The individual can reproduce posterity every time. The proportion of the infected babies is p_I.

(v) The death rate of infected is α,the recovery rate of infected is γ.

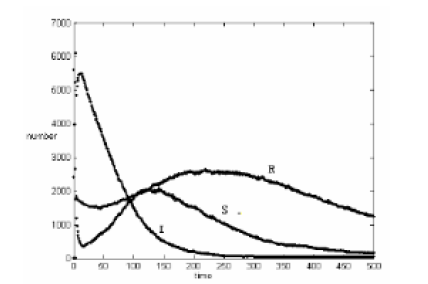
The algorithm-systemic structure of this kind of epidemic diseases model is shown in Figure 2 with its two computational configuration schemes illustrated in Figures 3 & 4. Notice however, the epidemic evolutions as observed at the time  which were computed by the constructed CA with the transition rule [10,40], these are presented in Figures 5 & 6. Therefore, these figures shed more light into the computational insights thus into the computational discrete-event dynamics the CA-based epidemic models.

Figure 2: Algorithm-systemic model structure of the epidemic diseases characterized by vertical transmission and contract.

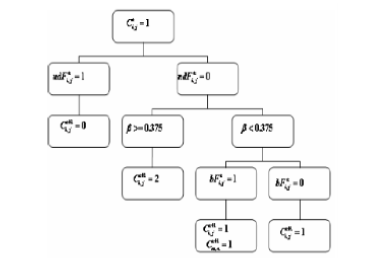
Figure 3: Status C^t=1_i,j at time t +1 of the computational configuration exploring phenomena vertical transmission and contract epidemic from when it was , C^t_i,j = 1 .

Figure 4: Status C^t=1_i,j at time t +1 of the computational configuration exploring phenomena vertical transmission and contract epidemic from when it was , C^t_i,j = 0 .

Figure 5: Evolution of the infected population number, deathrate of infective population is 0.25.

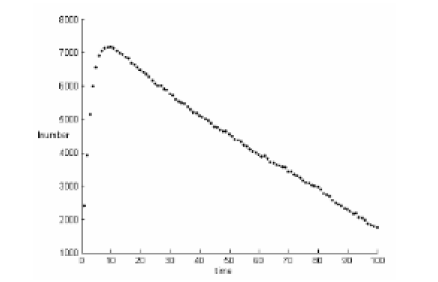
Figure 6: Evolution of the susceptive population number when death-rate of infective population is 0.25.

Here for an arbitrary cell state there is adopted: s_ij⋅s_ij=1 and represents empty state; while s_ij=1 represents state of susceptive individual; s_ij=2 represents a infected one; and s_ij=3 represents state of a recovered individual. Then the configuration of time t in the CA-based model is described by instantaneous automaton state:

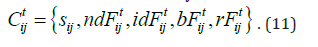
Here ndF^t_ij represent a flag called the "natural death flag". The value of this flag indicates whether the individual located in the cell (i,j) has reached natural death at time t. If ndF^t_ij=1, the individual located in the cell is natural death at time .

Also, the following indications and meanings should be noted further:

If nF_ij=0, the individual located in the cell (i,j)is not in natural death at time .

if_ij is a flag called the "infectious death flag". The value of this flag indicates the infectious individual located in the cell (i,j) is infectious death at time t.

bF_ij is a flag called the "birth flag". The value of this flag indicates the individual located in the cell (i, j) will generate offspring at time t.

rF_ijis a flag called the "recover flag". The value of this flag indicated the infectious individual located in the cell is (i, j) recovered at time t.

Computer simulations results

The cellular space of the CA based model the simulations was formed by a two-dimensional array of 100x100 cells. The proportion of population is 80%. For the sake of simplicity, it was assumed to use the following artificially chosen parameters: d = 0.006, b=0.012, γ = 0.3. These simulation results are depicted below.

When α= 0.25, if the number of recovered states is zero, the epidemic will outbreak at time t = 3 as simulations show in Figures 5 & 6.

Finally, when p_I=0.80, the epidemic reaches the inherent steady state at the instant of 300 time-units as Figure 9 demonstrates. It should be noted however, it takes a considerably long time of propagation spread until this steady state is being reached and established as equilibrium state.

Figure 7: Evolution of the susceptive population number when death-rate of the infective population is 0.01.

Figure 8: Evolution of the infected population number, death-rate of infective population is 0.01.

Figure 9: Evolution of the SIR population number with the vaccination accomplished before the epidemic.

DoA Estimation For SIRS Epidemic Dynamics

First certain definition and a lemma are introduced in here; also, see [5,41,12,3,39,45].

Definition 1. Consider the following nonlinear system

where 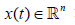represents the state vector of the system and f(x) is a polynomial function of the state vector. Let 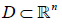be a domain containing the equilibrium state point x = 0 of the system (6). Let be a continuous function. If the allowing condition is satisfied,

then the system (6) is locally asymptotically stable in equilibrium at origin x = 0, and denotes 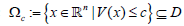is the positively invariant region.

Lemma 2 [8]. If there exists the continuous, differentiable and positive definite function , satisfying

the solution of the system (6) for all x(0)∈ D can be obtained, and , 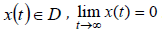. D is the subset of the DoA of (6).

If the Lyapunov conditions for local asymptotic stability are sought for, then construction of the SOS programming is needed in order to prove the fixed point stability. Additionally, this technique can be used to find and maximize the size of certain invariant subsets of its region of attraction. According to Lemma 1, the system (6) is locally asymptotically stable in P₂(p₁,p₂,p₃), so we can estimate the DoA of SIRS epidemic model based on SOS optimization.

First, let suppose that x = S + p₁ , y = I + p₂ , z = R + p₃, and then the equivalent model can be constructed as

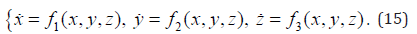
In order to expand the set D, we define a region 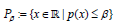, which contains the state variables and maximizes β, satisfying 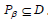. In this way, the DoA problem is transformed into the optimization problem (16).

Let assume constructing the equivalent constraints for x ≠ 0 at cases l₁ (x) ≠ 0 , l₂ (x) ≠ 0 , l₁,l₂ ∈Σ_n where Σ_n is some functional space of real-valued parameters. Then optimization scheme described with (16) is transformed as related to condition of empty set ∅ .

It should be noted, it is possible to get for problem (17) the constrained condition of SoS optimization which is simplified through Psatz Theorem and Generalized S-procedure [30,35,36]:

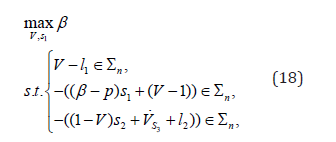
where l₁ , l₂ ∈Σ_n , s₁ , s₂ , s₃ ∈Σ_>n.

Remark 3. Problem (18) is a bilinear programming problem hence it can be compute by using SOSTOOLS and PENBMI [47] that are used for solving the bilinear SDP problems. The set domain of attraction 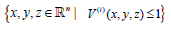along with Lyapunov functions V⁽ⁱ⁾(x, y, z) (the LF) can be computed according to (18); here i is the number of iterations that may be needed.

DoA Case Study Example: Simulation Results/ and Comparison Analysis

An illustrative example is explored in this section via fixing coefficients to certain numerical values, computer simulations and a comparison discussion.

Model for a numerical case study

A numerical case-study is constructed by assuming values , α = β = γ =δ = c = d = 1/ 2 , A = 4, and then R₀ = 2 > 1 [8,9]. The obtained system model has the form of the following systems of differential equations:

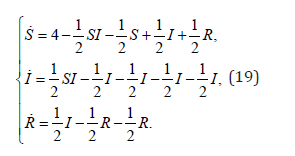
Let assume suitable fixed values 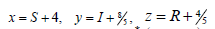hence . The latter can be transformed into P*₂(0,0,0). Then the system model can be represented in the following form:

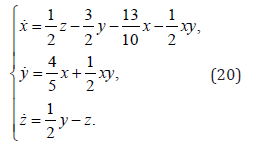
The condition of the domain of attraction for (20) satisfies:

x ≥ −4, y ≥ −8 / 5, z ≥ −4 / 5

Next, suppose the highest degree values in variables and quantities in V, l₁,l₂ , and s₁,s₂,s₃ can be defined by assuming the relevant constant as presented below:

Then the Lyapunov function  [12] can be computed employing SoS optimization technique by using SOSTOOLS box [2], and it found as follows:

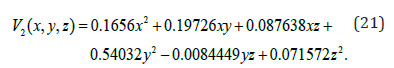
Thus the actual attraction domain of system 19 (13) can be computed as a set defined by model:

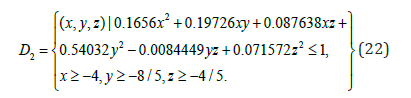
Further Discussion and Comparison

With reference to the LF-LMI optimization based on moment theory and the SOS optimization approaches when applied to the estimation of DOA for the epidemic model may be establishes as in the sequel.

Firstly, let Lyapunov function V₁ = V₁(x y z) be chosen as follows:

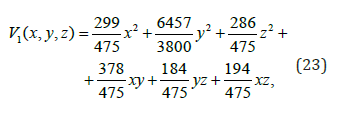
Then the region DoA of system (13) can be computed by using GloptiPoly-Box of Henrion and Lassere [43]. It was found as the following subset:

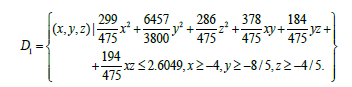
As the now domain of attraction obtained is an irregular sphere, in this case application software Mathematica is used to obtain the simulation results of the DoA for the SIRS epidemic model based on both the Lyapunov function (LF) and the SoS optimization theories. Those results are depicted in Figure 10.

Remark 4. Equations 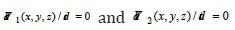give stability region boundary of the SIRS epidemic model.

Figure 10: Enlarged relative to previous DoA of SIRS model based on Lyapunov theory and SoS optimization methods [4].

Figure 11 illustrates the analysis of the obtained DoA by means of those two optimization approaches. It is readily seen from both figures that the DoA obtained by the approach argued for in this study is larger than that domain of attraction using the randomly selected Lyapunov function of LMI approach. Simulation result demonstrates enlarged DoA using SoS optimization is found in compared with Lyapunov theory approach. It is an issue for future research to what extent it may a viable enlarged DoA could be found to expand.

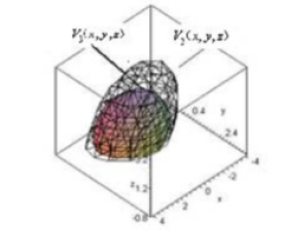
Figure 11: Enlarged inner domain relative to the previous DoA of SIRS epidemic model based on LMI optimization with moment theory and SoS optimization [4].

It should be noted that Li, et al. [28] also gave an LMI optimization approach to investigate the estimation of DoA of a class of SIRS models using LF-LMI approach based on moment theory [46]. Their technique produced the DoA of SIRS model as determined by V₃ = V₃(x y z) in Figure 11. The concluding simulation results of DoA for SIRS epidemic model using the LF-LMI with moment theory optimization and the SoS optimization methods are depicted in Figure 11.

Remark 5. The internal ellipsoid is the three-dimensional map of the domain of attraction of the SIRS model computed via the moment theory [11,46]. And the outside grid three-dimensional map is computed by means of the SOS optimization algorithm [8,9,2].

In fact, Figure 10 illustrates a kind of comparison analysis of the computable DoA by the two optimization approaches by more details. Due to preselected Lyapunov function using the LMI method with the momentum theory, the algorithm appears static. The SoS optimization technique however provides a dynamic iterative solving algorithm for optimum Lyapunov function choice. Thus, operationally the algorithm is dynamic too. It can be seen from Figure 11 furthermore the enlargement of the domain of attraction of SIRS model using SoS optimization, as compared to that of LF-LMI optimization based on moment theory, is obtained too and at the same time higher accuracy is achieved. Though precision appeared relatively low when high-dimension systems (n ≥ 3) are dealt with. Thus, the SoS optimization algorithm is worth for investigating the high-dimensional systems (n ≥ 3), because the DoA found can be even larger. Though, the computing speed becomes rather slow.

Concluding Remarks and Future Research

The CA-theory based computational model for the epidemic having characteristic feature of vertical transmission and contract has been built. It is based on the proposed two-dimensional cellular model that can be considered as an alternative SIR-type model of epidemic propagation.

It is characterized by the several innovated features, which are assumed as an essential background features of this technique. First of those innovated features is the assumption the total amount of population in the cellular space is not constant. Second, the local transition function is simple and only several epidemiological and environmental parameters are involved. And thirdly, the time of the stable steady state of epidemic spread with vertical transmission characteristic and contact is also computed. The proposed CA model is believed to be a proper basis for future investigation of the underlying phenomena of the dynamics of real-world epidemics because the vaccination effect has been considered.

The DoA of a class of SIRS epidemic dynamic models, which has been shown rather useful in real-world applications, has been investigated by using both SOS optimization and LF-LMI approaches. The computation was performed by using the semi-definite optimization tool ‘SeDuMi’. The viability of all these ideas is confirmed by considerable success in applying it to the typical theoretic model. In addition, numerical and simulation results of the proposed SoS optimization approach were compared with those of the Lyapunov-function LMI technique. Thes ellipsoid shape of DoA is realistic reasonably while the computational burden is drastically reduced (compared to the pure Lyapunov ‘blind search’). A task for the future research on DoA is to explore the recent result on DoA estimation for large-scale nonlinear systems [25].

In fact, the analysis introduced in this paper played an important role in investigating the outcome predicted by disease model. It has been shown to provide valuable information for analyzing the spread mechanisms of infection and diseases, and also for forecasting the future trends of infectious diseases. It can help to assess the effectiveness of prevention, treatment and control programs, such as education, health, vaccination, quarantine, and other activities of social responsibility. Further, it is believed both approaches are applicable in other epidemic models beyond the SIRS, which is a topic for future research [13,22,43,53-56]. Yet it remains to be explored to which extent the findings of this paper are indeed relevant for analyzing real-world accidents of epidemic/pandemic diseases spreads.

Acknowledgement

The authors acknowledge contributions by the former Ph.D. researchers C.-L. Chang, X. Chen, C. Li, at NEU of Shenyang, and V. M. Ojleska, at Saints C&MU in Skopje, to computing algorithms and simulations to investigate epidemic/pandemic dynamics and spreads propagation.

Funding

This research has been supported by National Natural Science Foundation of P.R. China to College of Information Science in Shenyang, and in part by Fond for Science of Doctoral School FEIT, Saints Cyril & Methodius University in Skopje, R. N. Macedonia.

References

• (2023) General Assembly of North Carolina. Session 2015. Session Law 2015-245, House Bill 372: An Act to Transform and Reorganize North Carolina’s Medicaid and NC Choice Programs.
• (2021) NC Medicaid Managed Care. North Carolina Department of Health and Human Services.
• Keast SL, Skrepnek G, Nesser N (2016) State Medicaid Programs Bring Managed Care Tenets to Fee for Service. J Manag Care Spec Pharm 22(2):145-148.
• (2023) NC Medicaid Enrollment Reports. North Carolina Department of Health and Human Services.
• Allen EH, Johnston EM, Courtot B, Caraveo CA, Gonzalez D, et al. (2022) North Carolina Medicaid’s Transition to Risk-Based Managed Care. Urban Institute.
• Aijaz M, Song PH, Winslow HC, Jackson J, Lewis VA, et al. (2022) Continuity through Disruption: Beneficiary Engagement Strategies during the Transition to Medicaid Managed Care in North Carolina. Academy Health Annual Research Meeting.
• Allen EH, Johnston EM, Courtot B, Caraveo CA, Gonzalez D, et al. (2022) North Carolina Medicaid’s Transition to Risk-Based Managed Care. Urban Institute.
• Zimmer RP, Hanchate AD, Palakshappa D, Sheena McNeill, Charlotte I. Crotts, et al. (2023) Perceptions of North Carolina’s Medicaid Transformation: A Qualitative Study. North Carolina Medical Journal 85(6).
• Katella K (2021) Our pandemic Year-A COVID-19 Timeline. Yale Medicine.
• (2024) Mayo Clinic. Engaging Black and African American Populations.
• Henry Akintobi T, Jacobs T, Sabbs D, Holden K, Braithwaite R, et al. (2020) Community Engagement of African Americans in the Era of COVID-19: Considerations, Challenges, Implications, and Recommendations for Public Health. Prev Chronic Dis 17: E83.
• Berg S (2020) 7 ways to improve Black health-in mind and body.
• Cramer ME, Lazoritz S, Shaffer K, Palm D, Ford AL (2018) Community Advisory Board Members’ Perspectives Regarding Opportunities and Challenges of Research Collaboration. West J Nurs Res 40(7): 1032-1048.
• Newman SD, Andrews JO, Magwood GS, Jenkins C, Cox MJ, et al. (2011) Community advisory boards in community-based participatory research: a synthesis of best processes. Prev Chronic Dis 8(3): A70.
• Wilson C (2018) Grassroots Community outreach and engagement.
• (2024) North Carolina's Transformation to Medicaid Managed Care. North Carolina Department of Health and Human Services.
• (2023) View health plans. North Carolina Department of Health and Human Services.
• (2023) Questions and Answers about Medicaid Expansion. North Carolina Department of Health and Human Services.
• Mbe KA (2017) Culturally Competent Health Education in African Americans’ Faith-based Communities for Better Health Outcomes: A Literature Review. McNair Research Journal SJSU 13.
• Linnan LA, Ferguson YO (2007) Beauty Salons. A Promising Health Promotion Setting for Reaching and Promoting Health Among African American Women. Health Educ Behav 34(3): 517-530.
• Brewer LC, Williams DR (2019) We've Come This Far by Faith: The Role of the Black Church in Public Health. Am J Public Health. 109(3): 385-386.
• Hays K, Aranda MP (2016) Faith-based mental health interventions with African Americans: A review. Research on Social Work Practice 26(7): 777-789.
• Markens S, Fox SA, Taub B, Gilbert ML (2002) Role of Black churches in health promotion programs: lessons from the Los Angeles Mammography Promotion in Churches Program. Am J Public Health. 92(5): 805-810.
• Moore T (1991) The African American church: A source of empowerment, mutual help, and social change. Prevention in Human Services, 10(1): 147-167.
• Pratt CC, McGuigan WM, Katzev AR (2000) Measuring program outcomes: Using retrospective pretest methodology. American Journal of Evaluation 21(3): 341-349.
• Gouldthorpe O Leary JL, Israel GD (2013) Capturing Change: Comparing Pretest-Posttest and Retrospective Evaluation Methods. 2013(1).
• Dalumpines L (2011) Objective types of test: Guidelines for writing completion questions and true-false questions.
• Treser M (2015) True/False Questions: Getting Them Right. Elearning Industry.
• Davis GC, Baral R, Strayer T, Serrano EL (2018) Using pre-and post-survey instruments in interventions: determining the random response benchmark and its implications for measuring effectiveness. Public Health Nutr 21(6): 1043-1047.
• (2024) The definitive place to explore US public data. DATA USA.
• (2023) Questions and Answers about Medicaid Expansion. North Carolina Department of Health and Human Services.
• (2023) When Can I Switch Health Plans. NC Medicaid Ombudsman.
• (2023) Managed Care. Medicare.gov.
• (2023) NC Medicaid Managed Care FAQs. UNC Health.
• Engel Smith L (2021) NC Medicaid managed care information blitz did not reach all enrollees. North Carolina Health News.
• Zimmer RP, Hanchate AD, Palakshappa D, et al. (2023) Perceptions of North Carolina’s Medicaid Transformation: A Qualitative Study. North Carolina Medical Journal. 84(6).
• (2021) As NC’s Medicaid managed care transition draws near, consumers express concerns and confusion. NC Health News.
• (2020) North Carolina Data. March of Dimes Peristats.
• Volpe VV, Schorpp KM, Cacace SC, Benson GP, Banos NC (2021) State- and Provider-Level Racism and Health Care in the U.S. Am J Prev Med 61(3): 338-347.
• Kennedy BR, Mathis CC, Woods AK (2007) African Americans and their distrust of the health care system: healthcare for diverse populations. J Cult Divers 14(2): 56-60.
• (2020) New Nationwide Poll by the Kaiser Family Foundation and The Undefeated Reveals Distrust of the Health Care System Among Black Americans. Kaiser Family Foundation.
• Okoro ON, Nelson CS, Witherspoon SP, Witherspoon SF, Simmons GE Jr (2020) Culturally Responsive Health Promotion to Address Health Disparities in African American Men: A Program Impact Evaluation. Am J Mens Health 14(4):1557988320951321.
• Daniels EC, Powe BD, Metoyer T, McCray G, Baltrus P, et al. (2012) Increasing knowledge of cardiovascular risk factors among African Americans by use of community health workers: The ABCD community intervention pilot project. J Natl Med Assoc104(3-4): 179-185.
• Peña Purcell NC, Jiang L, Ory MG, Hollingsworth R (2015) Translating an evidence-based diabetes education approach into rural African American communities: The “wisdom, power, control” program. Diabetes Spectrum 28(2): 106-115.