Short Communication 
 Creative Commons, CC-BY
Creative Commons, CC-BY
Application of Optimal Control Theory to Biomedical and Biochemical Processes
*Corresponding author: NU Ahmed, School of Information Technology and Engineering, University of Ottawa, Ottawa, Canada
Received: June 06, 2019; Published: June 19, 2019
DOI: 10.34297/AJBSR.2019.03.000683
Abstract
Optimal control theory is a highly developed subject. It has been applied in diverse fields of engineering, physics, economics, operation research, management sciences, policy planning etc. In particular, this subject has been successfully applied to bio-medical engineering problems like artificial heart, prosthesis. In this paper we present a brief summary of two recent papers on cancer immunotherapy and bio-reactors.
Introduction
In a recent paper [1] we proposed a dynamic model to represent the population of antigens and antibodies in cancer patients, in particular, the antigen-specific-antibody interactions to elicit immune response that leads to the death of cancer cells. The antibodies are known to be powerful medications for cancer immunotherapy. We published extensive numerical results in [2] demonstrating efficacy of the method. In another paper we considered bio-reactors and their optimal control and presented some interesting numerical results in [3].
Basic Principle of Immunotherapy
Mathematical modelling of bio-chemical processes has been widely used to study dynamic behavior of biological phenomena [4-6]. Results of such mathematical analysis can be used in both clinical and experimental settings. In the era of intense and rapid development of cancer immunotherapy, such efforts can prove to be significant in developing effective and efficient drug administration regimes and strategies. Currently, immunotherapy is the most promising and noninvasive cancer treatment approach compared to other well established therapies, such as chemotherapy. See the extensive references given in our paper [2]. The basic idea behind the immunotherapy is to use any feasible clinical technique that can enhance the patients immune system to destroy the antigens, for example, the cancer cells. This rapidly developing field of cancer immunology [4,5] has discovered new methods for treating cancer known as immunotherapy whereby the natural immune system of the human body is enhanced to fight cancer. The basic principles are briefly described as follows:
a. Checkpoint modulators: Here the idea is to block the ability of the so called checkpoint proteins from limiting the strength and duration of the natural immune response. There are several antibodies (IplimumAB, NivolumAB) which can act as immune checkpoint inhibitors.
b. Immune cell therapy: This immunotherapy is called ACT (Adoptive Cell Transfer). Here T-cells, infiltrating the tumor, called Tumor Infiltrating Lymphocytes (TILS), are col- lected from the patients tumor and cultured in the laboratory in large quantity and then activated by treatment with Cytokines and infused in the patients body which then attack and destroy the tumor cells.
c. Therapeutic Antibodies: Here antibodies are produced in the laboratory and linked to certain toxic substances (such as bacterial toxin). Such antibodies are called ADC (Antibody- Drug-Conjugates) and once they are administered to the patient, they bind on to cancer cells which absorb the toxic chemical leading to shrinkage and destruction of the tumor.
d. There are few other powerful techniques such as Cancer Treatment Vaccines and Immune System Modulators see [1].
Optimal Control of Immune System
In all the techniques as described above, antibodies are used to interact with antigens de- structively leading to annihilation of both and freeing the host body of toxin pathogens and cancer. We consider the dynamics of antibody-antigen interaction. In general, the dynamics of such systems is governed by a system of partial differential equations of reaction diffusion type. Let B stand for antibody and G for antigens. It is known that for each antigen there is a specific antibody that can bind on to and destroy it. So there are as many different antibodies as there are antigens. We assume that there are n different antigens and correspondingly n different antibodies. We denote their population densities by {Bi ,Gi ,i =1, 2,..., n} . The governing equations are given by the following system of partial differential equations defined on I × D where I = [0, T ] is the time domain and D ⊂ R3 denotes the spatial domain representing the patients tumor
These equations describe the temporal and spatial evolution of the antibodies and antigens. The parameters , {di ci} are the diffusion coefficients and Δ denotes the Laplacian in , R3,{αi} denote the production rates of antibodies by the natural immune system, βi, j is the interaction coefficient of the i-th antibody with the j-th antigen and γi,k is the production rate of antibodies induced by the control drug k u . If , γi,k =0 , the k-th drug has no contribution towards the production of antibody Bi. The parameters {δi} denote the intrinsic growth rates of antigens (for example cancer cells) and ηi, j denotes the interaction coefficient of the population of antibodies with the i-th antigen. The values of these interaction coefficients are generally negative. The objective is to promote the growth and strength of antibodies which can destroy the antigens. This is done by prescribing appropriate drugs (foods) for a period of time I [0, T] so as to eliminate the antigen population or bring it down to a harmless level. To achieve this goal one may choose the objective functional as
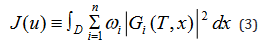
where {ωi>0} are the weights given to each of the
species of antigen population and u denotes the control vector u = {uk,k = 1,2, . . . , m}.The control drugs are subject to certain
clinical constraints such as the maximum admissible doses. This
constraint is described by a compact set 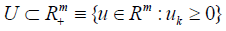 . The objective is to choose a control policy (a function of time) that
minimizes the above functional. This problem can be solved by
using the necessary conditions of optimality as given in [1, Theorem
4.1, p60]. This is computationally intensive. So for simplicity, in
our recent paper [2], we used the finite dimensional version of the
system of equations (1)-(2) by eliminating the diffusion coefficients
{di ci} . This approximation is valid if, either the diffusion
coefficients are significantly small, or the domain D is sufficiently
small so that one can consider the population density to be uniform
throughout the domain D.
. The objective is to choose a control policy (a function of time) that
minimizes the above functional. This problem can be solved by
using the necessary conditions of optimality as given in [1, Theorem
4.1, p60]. This is computationally intensive. So for simplicity, in
our recent paper [2], we used the finite dimensional version of the
system of equations (1)-(2) by eliminating the diffusion coefficients
{di ci} . This approximation is valid if, either the diffusion
coefficients are significantly small, or the domain D is sufficiently
small so that one can consider the population density to be uniform
throughout the domain D.
The simplified model is given by
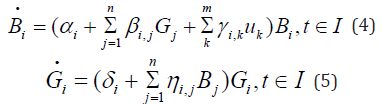
where now Bi, Gi are only functions of time. For the simplified (finite dimensional) model we used Pontryagin minimum principle to determine the optimal control prescribing the optimal doses as function of time. The numerical results are very encouraging and instructive. For details the reader is referred to [2].
Optimal Control of Bio-Reactors
There are many different bio-reactors. Some are designed for pharmaceutical industries to produce drugs. Another class of Bio-reactor is a system that can be used to degrade contaminants in ground water with microorganisms. It is used for waste water treatment. It is known that in a bioreactor the concentration of both bacteria and contaminants evolves in time and space. This can be described accurately only by a pair of partial differential equations of reaction diffusion type. However, we can consider the simplified model of a well- stirred bio-reactor where the population densities of bacteria and contaminants are spatially uniform but vary with time. The simplified system model is given by the following set of ordinary differential equations [3]:
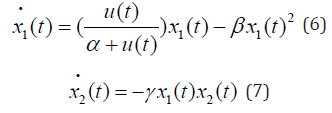
where the parameters {α ,β ,γ }are all positive, for example, {α = 0.5,β = 0.2,γ = 5}. The state 1x (t) denotes the concentration of bacteria while x2 (t) represents the concentration of contaminants all at time t. The concentration of input nutrient denoted by u(t) serves as the control variable. It is well-known that the bacteria degrades contaminants via co-metabolism, meaning that the degradation of the contaminants is a byproduct of the bacterial metabolism. The objective is to reduce the concentration of contaminants by the end of a given time period I ≡ [0,T] . So it is natural to consider the cost functional as
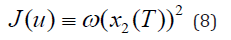
where w denotes the weight given to the level of concentration of contaminants. The optimal control was determined by using the necessary conditions of optimality developed in our paper [3, Theorem 4.2, p6]. For detailed numerical results the reader is referred to [3].
References
- NU Ahmed (2017) Optimal Control of Reaction Diffusion Equations with Potential Application to Biomedical Systems. Journal of Abstract Differential Equations and Applications 8(1): 4870.
- T Ahmed, NU Ahmed (2019) Optimal Control of Antigen-Antibody Interactions for Cancer Immunotherapy. Dynamics of Continuous, Discrete and Impulsive Systems Series B: Applications & Algorithms 26: 135-152.
- Shi’an Wang, NU Ahmed (2019) Optimal Relaxed Control for a Class of Nonlinear and Noncovex Dynamic Systems.
- M Linnebacher, C Maletzki (2012) Tumor Infiltrating B Cells. Oncoimmunology 1(7): 1186-1188.
- AM Scott, JD Wolchok, LJ Old (2012) Antibody Therapy of Cancer. Nat Rev Cancer 12(4): 278-287.
- S Tavoularis, A Sharapour, NU Ahmed, A Madrane, R Valliancourt (2003) Towards Optimal Control of Blood Flow in Artificial Hearts. Cardio Vascular Engineering 8(2).

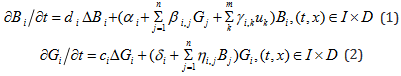


 We use cookies to ensure you get the best experience on our website.
We use cookies to ensure you get the best experience on our website.