Research Article 
 Creative Commons, CC-BY
Creative Commons, CC-BY
Comparative Osteology: A Cross-Species Study of First Rib Parameters and Their Relation to Body Mass with Emphasis on the Woolly Mammoth
*Corresponding author: AP Harrison, Department of Pathobiological Sciences, University of Copenhagen, Denmark.
Received: June 17, 2019; Published: June 24, 2019
DOI: 10.34297/AJBSR.2019.03.000690
Abstract
Scaling of body parts in relation to final adult body mass has been of interest for almost 300 years. However, it has been used quite recently to provide estimates of body mass for extinct species, for example the Woolly Mammoth (Mammuthus primigenius), based solely on isolated bones, mainly of limb origin. This manuscript addresses the discrepancies that appear when one uses different limb bones as predictors of body mass and examines the potential use of rib parameters as a means of improving the assessment of adult body mass in a range of diverse living mammals as well as the extinct Woolly Mammoth. The findings of this study have important implications for furthering our understanding of basic biology, physiology and scaling, as well as potential applications in terms of estimating body mass in the field of forensic science.
Keywords:Scaling; Lung capacity; Bone density; Forensic science
Introduction
Scaling addresses the structural and functional consequences of changes in size or scale among otherwise similar organisms. In terms of biology, one finds non-isometric scaling, often referred to as allometric which has its roots in the Greek term alloios meaning different. Indeed an amazing number of morphological and physiological variables can be scaled, relative to body size, according to the general allometric equation; y = a × Xb [1]. To the best of the authors knowledge, Galileo Galilei in his volume Dialogues Concerning Two New Sciences (1637) was the first to postulate that the skeleton and bones of very large animals must be scaled out of proportion to their linear dimensions in order to support the weight of the animal, and that the weight increases with the third power of linear dimensions. Logically, then if one assumes the legs of large animals simply serve as supportive “load bearing” columns, then it would be safe to assume that the greater the diameter of the said column, the greater the load it should be capable of bearing. However, one reaches a natural limit, as quite clearly the mass of an animal’s skeleton cannot increase out of proportion with body mass, at least not to the extent that the whole leg is comprised bone.
In a very recent study [2] it was shown that body height of an extinct species, namely the Woolly Mammoth (Mammuthus primigenius), could be derived from fossil remains, collected from the Flemish valley, according to the following formula; skeletal height = 4.35 * greater length of tibia (cm) + 12.7 cm [3]. Shoulder height was then estimated by adding a further 15 cm to the skeletal height to account for subcutaneous tissue and skin thickness [5]. Finally, the body mass of Woolly Mammoths was estimated using regression equations based on African elephants derived by Laws et al. [4], who computed from Ugandan elephant bulls that body mass (kg) 5.07×10−4 * SH2.803 where SH is shoulder height in centimeters. However, the findings of Christiansen [5] reveal a considerable degree of variation in terms of predicted body mass depending on which bone parameters and formulas are adopted as being the most suitable. For instance, tibia parameters recorded for the Hebior Mammoth (Mammuthus primigenius) which has a recorded shoulder height of 318 cm, estimated from its skeletal fossil remains, produced a body mass estimate that ranged from 4728 to 6852 kg [5].
Indeed, suggestions that Woolly Mammoths could have weighed as much as 8000 to 10000 kg or more, based on predictions from single limb bones have been made for the Brussels Museum and the Field Museum of Natural History in Chicago [5]. Interestingly, the heavier body masses are often associated with equations [5] that are applied to the humerus and femur bones rather than calculations that take their starting point from tibia measurements. Finally, there is an estimate of the body mass of Woolly Mammoth remains based on measurements of shoulder height [6], without making it at all clear as to what equations or constants have been adopted. Since oxygen consumption by body tissues must logically be related to body weight and since both the total number of alveoli in the lung as well as the total exchange surface are likely to be related to oxygen consumption, it is predictable that alveolar surface area should be related to body weight, which is indeed the case [7]. Furthermore, continuing this line of reasoning, the lung volume of a mammal constitutes approximately 5% of the body volume, irrespective of body size.
If a plot of lung volume (VL) in liters (dm3) is made against body mass (Mb) in kilograms a regression line with a slope of 1.06 is found, which represents a slight deviation from strict proportionality since larger animals tend to have proportionately larger lung volumes than smaller animals (thus 0.046 1.06 L b V = xM ) [8]. Furthermore, a test as to whether mass-specific pulmonary diffusion capacity for 02 ( o2 DL ) is proportional to mass-specific oxygen consumption o2 V , in such species as the horse and cow of body mass ~ 500 kg has already been investigated [9,10]. Indeed when one makes such a comparison it appears that, within a given size class (e.g. small, medium, large), o2 DL is closely matched to o2 V . Continuing with this comparative approach, it has also been consistently found that, over the size range of mammals ( 2 g < Mb < 1000 kg ), O2std V scales with 0.75 b M [8]. Indeed in support of which, Cook et al. [11] found that in terms of respiratory parameters, functional residual capacity was closely related over a range of body sizes to the height of a subject, raised to the power of 2.86.
In the light of the recent use of limb bones to predict body mass [12], and other studies with often wide ranging values, and sometimes apparently excessive estimates, this study has sought;
i. to establish whether parameters associated with the first rib, which helps define the shape of an animals rib-cage, can be closely related to body mass, and
ii. to investigate whether such a correlation might not be a better predictor of body mass than predictions of skeletal height based on limb bone (tibia) parameters.
Material and Methods
Measurements of first rib parameters (greater length – GL representing the outer curvature of the rib, lesser length – LL representing the inner curvature of the rib, medial circumference - MC) were taken from the skeletons of a number of species housed in the Dept. of Animal and Veterinary Basic Sciences, or made available to the author through the kind assistance of Copenhagen Zoo, Scandinavian Animal Park Djursland, and Oxford University Museum. Thereafter, skeletal (shoulder) height and body mass were either measured or recorded from notes kept about the specimens. In total, nine species were measured, including a lion, a cow, a goat, a giraffe, a horse, a female human, a rhinoceros and an Asian elephant. Measurements were taken by hand with care being made to avoid excessive handling of museum specimens, yet at the same time ensuring that accurate recordings were taken. The greater and lesser lengths of the ribs were used to arrive at a medial bone length, and it was at this derived mid-point along the length of the bone that the measurement of medial circumference was taken. Any remaining fossilized cartilage was not included in the greater and lesser length measurements. A similar procedure was then followed for the measurements of tibial length and its medial circumference, where these measurements were possible.
The measurement of skeletal height was taken from the spine at the region between the shoulder blades, for most of the mammals measured, however, in the case of the female human skeleton, the height was taken as being the distance between the base of the heel and the crown of the skull. The collected 1st rib measurements, when plotted, were found to best fit a polynomial (first order; see below) equation where rib parameters GL, LL and MC (cm) were related to the intercept plus the slope times the body weight (kg).
Equation 0: Polynomial first order (linear )Y = Intercept + Slope* X
Data were plotted using Prism 4 for Macintosh (version 4.0b, 2004), and the same software was used to analyze the curve of the plot as well as determine any significance with regard to the fitted equation.
Bone Mineral Density & Bone Mineral Content
A total of 4 Mammoth bones and the identical bones from an adult Indian Elephant were measured for their bone mass density - BMD (g/cm2) and bone mineral content -BMC (g) using a DEXA scanner with both the Total body scan program for the larger bones (tibia, rib, lumbar vertebra), and the Small animal program for the phalanges (GE Luna Prodigy, Madison WI, USA, encore 2005 software, version 9,15,010).
Statistical tests
Values are presented as means ± SEM. Differences between means were tested for statistical significance with the use of a oneway ANOVA and an additional test for Gaussian Normal Distribution (GraphPad Instat 3 for Mac; Version 3.0b, 2003; Graph- Pad Inc., La Jolla, CA). Data were found to be normally distributed and to have equal variance. Differences showing a P value >0.05 were considered non-significant.
Results
Correlation of rib parameters with body mass
The measurements of Greater Length (GL) for the first rib of the species examined were found to be best fitted by the following equation;
Equation 1: GL (cm) = 8.53+ 0.02236*Body Mass (kg )
The measurements of Lesser Length (LL) for the first rib of the species examined were found to be best fitted the following equation;
Equation 2: LL (cm) = 7.48 + 0.01265*Body Mass (kg )
Finally, the measurements of Medial Circumference (MC) for the first rib of the species examined was found to be best fitted the following equation (See Figure 1);
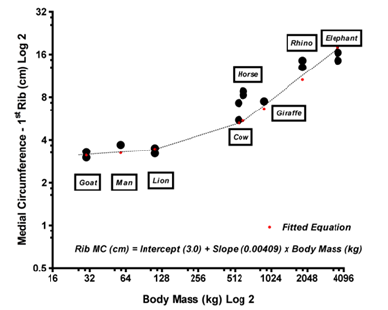
Figure 1:First rib - medial circumference parameter (Log2) measurements versus body mass (Log2): a cross-species correlation. The best fit equation derived from the recorded data is given, as is the best fit curve – small red dots joined by a faint dotted line. See the results section for equations. The 95% confidence interval for the slope was found to be between 0.00335 and 0.00483 (mean = 0.00409 ± 0.00034). The fit of the curve was found to be significant P<0.0001 with 14 df.
Equation 3: MC (cm) = 3.00 + 0.00409*Body Mass (kg )
A goodness of fit test revealed an R2 of 0.83, 0.69 and 0.94 (all with 14 degrees of freedom), for equations 1, 2 & 3, respectively (Figure 1).
First rib and tibia measurements for Woolly Mammoth fossilized specimens
Of the two fossilized first ribs and tibia specimens accessible to the author, only one of the tibia bones was from a fully grown adult, the other bones were from juvenile Woolly Mammoths, judging by the lack of cartilage at the bone ends. The first ribs were found to have the following parameters; GL = 46.0 cm, LL = 45.5 cm, MC = 11.3 cm, and GL = 50.5 cm, LL = 48.5 cm, MC = 14.0 cm. Measurements for the two fossilized Woolly Mammoth tibia bones were as follows; GL = 54.5 cm, MC = 26.5 cm and GL = 68.5 cm, MC = 35.0 cm. Thus, using Equation 3 and the MC measurements for the first ribs of the two Woolly Mammoths, it was possible to arrive at an estimate of average body mass for the two extinct animals. For the smaller of the two fossilized Woolly Mammoth first ribs an estimated body mass of 2029 kg was calculated (MC = 11.3 cm). Similar measurements for the second of the two fossilized Woolly Mammoth first ribs gave an estimated body mass of 2689 kg (MC = 14.0 cm).
Tibia parameters as an estimate of body mass
In order to assess the often used tibia-length-based equation for skeletal height (Equation 4), and body mass (Equation 5), subsequently derived from skeletal height, this study chose to examine a number of large species, of known body mass, among them the Asian elephant Coco, which had lived for many years at Copenhagen Zoo (born 22-01-1986 and died 21-09-2003).
Equation 4: Skeletal Height = 4.35*Tibia Length(cm) +12.7cm
Equation 5: Body Mass (kg ) = 5.07x10−4 *Skeletal Height2.803
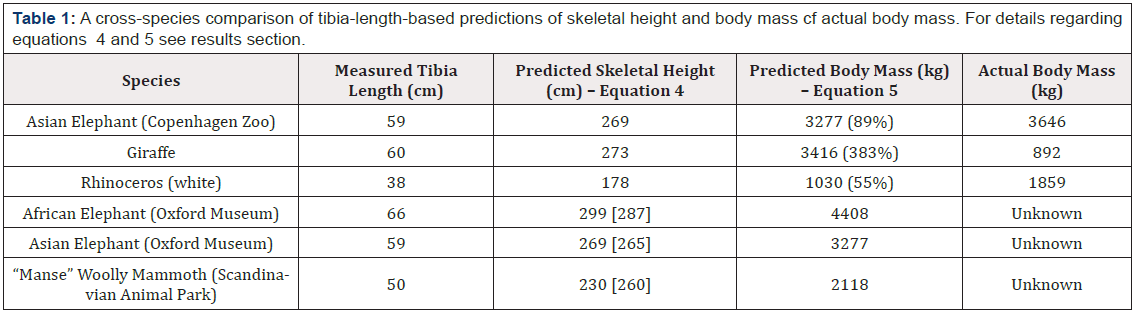
Table 1: A cross-species comparison of tibia-length-based predictions of skeletal height and body mass cf actual body mass. For details regarding equations 4 and 5 see results section.
Note: () = percentage of actual body mass, [] = measured skeletal height.
The Asian elephant Coco had a tibia length of 59.0 cm with a medial circumference of 24.5 cm (diameter = 7.8 cm) and represented a mature adult male with a body mass of 3646 kg. Thus using the equation of Germonpré et al. (Equation 4) [2] a skeletal height of 269 cm, cf. an actual value of 259 cm, was predicted, and using this value in the equation of Laws et al. (Equation 5) [4] it was possible to arrive at a predicted body mass of 3277 kg, which was some 369 kg lighter than the actual animal. Thus, the methodology of estimating skeletal height from tibia length, followed by the use of the derived skeletal height value to predict body mass proved to be 89% accurate in this instance. It should be noted that in a recent study, the ratio of tibia length to predicted skeletal shoulder height was found to be 23.2% for Mammuthus primigenius, and in this study we arrived at a value of 21.7%, which is in close agreement [13] (Table 1).
Using equations 4 & 5, which appear to be 89% accurate for modern day Proboscidae of the Elephas (Eurasian elephant) genus, one might be able to derive some estimate of body mass when taking into account a fossilized Mammoth tibia with a length of 68.5 cm and a medial circumference of 35.0 cm (diameter = 11.1 cm). Indeed, equation 4 predicts a skeletal height of 310 cm, and equation 5 subsequently returns a predicted body mass of 4878 kg for the Woolly Mammoth (Mammuthus primigenius) whilst alive.
Alternatively, the following equation;
Equation 6: L * d2 = Mb
has been used to estimate body mass (Mb), taking into account not only bone length (L in cm) but also its weight bearing properties as represented by its diameter (d in cm). Using equation 6 one derives a body mass for a 59.0 cm long and 7.8 cm diameter tibia from Coco the Asian elephant at Copenhagen Zoo of 3589 kg, which in this instance proves to be 98% accurate. Likewise, the use of equation 6 derives a body mass for a 59.0 cm long and 6.7 cm diameter tibia from the Giraffe of 2648 kg, which represents 296% of the actual body mass (892 kg). However, when one turns to the Rhino, and applies equation 6 for a 38.0 cm long and 7.1 cm diameter tibia, a body mass of 1915 kg is predicted, which compares favourably (103%) with the actual body mass (1859 kg) for this animal.
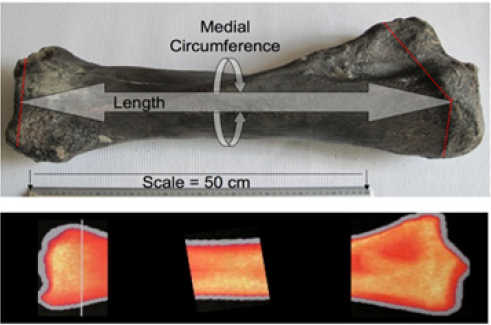
Figure 2:Tibia – Woolly Mammoth fossil. This tibia is from an adult male and was found, caught in fishing nets, in the North Sea just off the Dutch coast. The length and medial circumference sites are identified by the white arrows, whilst the red dotted lines represent the region of fossilized cartilage which were not included in the overall length measurement. The scale bar represents 50 cm. Bone Mineral Density images are courtesy of Prof. Klaus Ølgaard & colleagues, Rigshospitalet, Dept of Nephrology and Endocrinaology, Blegdamsvej 9, Copenhagen DK 2100 Ø, and were made using a Norland DEXA scanner. Authors private collection.
Finally, returning to the fossilized Woolly Mammoth tibia with a length of 68.5 cm and a medial circumference of 35.0 cm (diameter = 11.1 cm), and using the alternative equation (Equation 6) of which seems to be a fairly accurate predictor of body mass in the Asian elephant Coco, a body mass for the Woolly Mammoth of 8500 kg is then derived (Figure 2).
In order to further validate these equations, the authors took measurements from the first ribs and tibia of an almost complete Woolly Mammoth skeleton at the Scandinavian Animal Park outside Kolind, Denmark. This specimen, known affectionately as “Manse” appears to be of a juvenile, with a skeletal height of 260 cm. Using equation 4 and a measured tibia length of 50.0 cm, a skeletal height of 230 cm was derived for “Manse”, representing 88.4 % of the actual measured skeletal height. Continued use of the estimated 230 cm skeletal height in equation 5 yielded a body mass of 2118 kg, whilst use of the actual 260 cm skeletal height gave a value of 2979 kg. However, use of the first rib measurements from “Manse” (MC = 16.0 cm) and equation 3, predicted a body mass of 3178 kg. The combined use of tibia length and diameter (50.0 and 8.4 cm, respectively) in equation 6 estimated a body mass for “Manse” of 3528 kg.
In contrast, measurements taken from a wild adult male African elephant to be found at Oxford University Museum of Natural History, gave a tibia length of 66.0 cm and a diameter of 9.7 cm, a first rib medial circumference of 16.5 cm and a skeletal height of 287 cm. Using equation 4 a skeletal height of 299 cm was derived for the Oxford African elephant representing 104.0 % of the actual measured skeletal height. Continued use of the estimated 299 cm skeletal height in equation 5 yielded a body mass of 4408 kg. However, use of the first rib measurements (MC = 16.5 cm) and equation 3, predicted a body mass of 3300 kg. Finally, the combined use of tibia length and diameter (66.0 and 9.7 cm, respectively) in equation 6 estimated a body mass for the Oxford African elephant of 6209 kg.
Bone Mineral Density
The BMD and BMC values for the selected Mammoth and Elephant bones measured in this study are to be found in Table 2. Whilst these have been measured as accurately as possible, the fact remains that the BMC, in particular for the first rib, may be an underestimate of the true value due to leaching of minerals to the North Sea. Moreover, this explanation would fit with the findings of a higher BMC in the vertebrae and phalanges of the Woolly Mammoth cf values obtained for the Asian Elephant (Table 2).
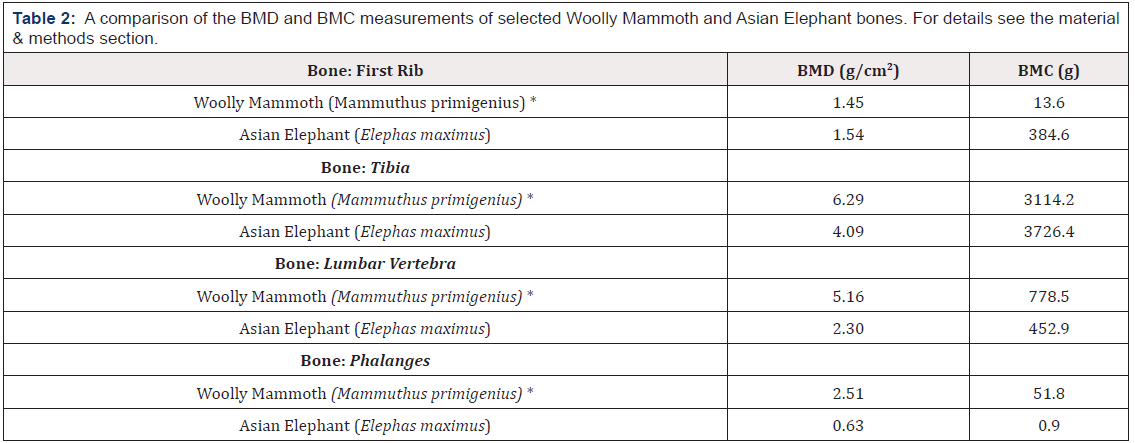
Table 2:A comparison of the BMD and BMC measurements of selected Woolly Mammoth and Asian Elephant bones. For details see the material & methods section.
Values marked with a * represent measurements taken from bones collected from the North Sea.
Discussion
The results of this study clearly show a good correlation between the medial circumference (cm) of the first rib of the mammals measured and that of their body mass. This novel scaling equation provides an additional tool for those working with comparative aspects of biology and physiology, for those involved in the assessment of museum specimens and fossil remains, as well as those working in the field of forensic science all of which, from time-to-time, assess incomplete skeletons in terms of predicting an individual´s height whilst alive. Moreover, to the authors knowledge, this is the first time that an equation based on respiratory-linked parameters has been used to assess the body mass of Woolly Mammoths.
Scaling issues
The issue of scalability in animals is a very fascinating topic, and one that is grounded in a wish to compare animal size at the level of common denominators. There are a great many papers that address this topic and nearly as many equations. Indeed in addition to those equations mentioned so far, one should also mention the work done in the 1970´s by McMahon, who showed that for any supporting bone, the diameter (d) scaled with the 3/8th power of the body mass (Mb), and the length (l) scaled with 1/4th the body mass [14]. However, it is important that one should also consider scaling in terms of elasticity, that is to say the properties a bone has to withstand bending forces. It is the property of elasticity that enables a bone to maintain its shape without distortion arising from an imposed and often very sudden stress or load. Failure to maintain such an elastic property results of course in buckling and fracturing. Thus the critical variables that need to be considered are not only the length and diameter of a given bone (column), but also the elastic modulus of the material used. This being said, it is known though that bones of different animals have the same material composition, crystalline calcium apatite embedded in a matrix of collagen, and that surprisingly, measurements of failure stress in bones of mammals ranging from 50 g to 700 kg body weight (a 14,000-fold range) have very similar values; 233 ± 53 MN/m2 – small versus 200 ± 28 MN/m2 – large animals [15]. The BMD measurements show the lowest values 1.9 g/cm2 for the rib, and the highest values 8.2 g/cm2 for the vertebra, with the tibia ranging 6.2 to 7.1 g/cm2.
The body mass of elephants has been shown to be much less than the estimated weights of adult Wooly Mammoths [16], which may be possible to see from not only their skeletal dimensions, but perhaps also their bone structure, in particular their BMD. This study has shown that a BMD comparison of the first rib are very similar for both elephants and Woolly Mammoths (1.45 versus 1.54 g/cm2), however, this is not true of the other bones looked at. The tibia, lumbar vertebra and the phalanges of the Woolly Mammoth were all found to have a higher BMD than those of the elephant. The BMC values are far from conclusive. The Mammoth rib has a much lower value than the elephant, perhaps due to leaching of minerals to sea water, as this sample was found in the North Sea. In contrast the tibias have a very similar BMC, despite the Mammoth samples also being sourced from the North Sea, although they may have been less exposed than the rib, perhaps covered with silt. Then there are the BMC values for the lumbar vertebra and the phalanges, both of which are higher in the Mammoth compared with the elephant, perhaps lending weight to the greater body mass of Mammoths cf Elephants?
Perhaps of greater relevance in terms of this study, is the finding that body mass can be scaled to the medial circumference of the first rib of a number of animals. This is perhaps not so surprising since lung tissue represents allometrically 1.13 0.01 b M − of body mass [17]. Thus when one plots the log of lung volume for small and large animals alike against the log of body weight, one finds that a straight-line correlation is achieved, with a regression line slope of 1.02. Put another way, mammalian lung volume (Vl in ml) relates to body mass (Mb in kg) in the following way; 53.5 1.06 0.02 l b V = M ± [18] (Figure 3).

Figure 3: First rib – Upper Panel: a comparison of an isolated Woolly Mammoth first rib alongside a complete and single Mammoth skeleton to be found on display at the Scandinavian Animal Park (Djursland, Nødager, Kolind, Denmark) – inset panel shows the two first ribs alongside one another. Note how similar they are in size and length. Lower Panel: a comparison of an isolated Woolly Mammoth first rib alongside the complete skeleton of the Asian Elephant Coco to be found on display in Copenhagen Zoo (Denmark) – inset panel shows the Elephant and Mammoth ribs alongside one another.
Appropriate body mass equations
The issue still remains, however, as to which equation should one choose when attempting to predict body mass? Whilst this study has introduced a new equation based on the medial circumference of the first rib and shown that this can serve as a good predictor of body mass in a number of species, an attempt has also been made to validate existing body mass predictors. To this end an assessment of tibia length as an estimator of skeletal height has been investigated, and the accuracy of this two-tier system, employing an equation to estimate skeletal height, followed by a second equation using the estimated skeletal height to finally predict body mass, has been made. This study has found that this two-tier equation system works very well for elephants, but then this system was derived using elephant data, so this is perhaps not so surprising. When equations 4 and 5 are applied to giraffe and rhinoceros tibia data, the accuracy of the body mass prediction is less than ideal; gross over estimation for the giraffe compared with 50% underestimation for the rhinoceros. Clearly, then this two-tier system appears to be more or less species specific, which begs the question as to whether it is suitable for assessing the body mass of Woolly Mammoths?
In defence of the two-tier system, one has to acknowledge that equation 4 proved an accurate predictor of the skeletal height of the African and Asian elephants on display at Oxford University Museum of Natural History, which is interesting as the African elephant was captured from the wild. It is also worth noting that equation 4 serves as a very accurate predictor of skeletal height for “Manse” the adolescent Woolly Mammoth skeleton on display at the Scandinavian Animal Park, Djursland. The combined use of not only bone length but that of bone diameter in equation 6, does seem to improve the accuracy of body mass prediction. In the case of “Coco” the Asian elephant skeleton on display at Copenhagen Zoo, equation 6 improved body mass prediction from 89% to 98%. This equation also proved a very accurate predictor of body mass in the rhinoceros, taking the 55% body mass prediction of equations 4 & 5 to a103% accuracy. Of particular interest, however, is the fact that equation 6, whilst an improvement on the prediction made by equations 4 & 5, still grossly overestimated the body mass of the giraffe (296%). Perhaps then equation 6 is only accurate as a predictor of body mass in so long as the animal in question is rather robust, compact and solid in structure?
Finally, validation of the aforementioned equations in terms of fossilized remains, and in particular the skeletal height and body mass predictions for Woolly mammoths, continues to provide mixed results. In the case of “Manse” the Woolly Mammoth skeleton on display at the Scandinavian Animal Park, Djursland, equation 4 was able to predict skeletal height with a degree of accuracy equivalent to 88%, and equation 5 predicted a live body mass of 2979 kg. When equation 3 was used to predict body mass based on first rib medial circumference, a body mass of 3178 kg was arrived at. However, use of equation 6, which has proved the most accurate assessor of body mass in both the elephant and rhinoceros, derived a predicted live body mass of 3528 kg for this adolescent Woolly Mammoth. This final value is interesting as it equates to the final adult body mass of a male Asian elephant, and perhaps implies that Woolly Mammoths were appreciably heavier than modern day elephants. Indeed, this thought is supported by the body mass prediction arrived at when equation 6 is used on the fossilized tibia measurements of what must have been a large adult Woolly Mammoth; some 8500 kg, which is considerably heavier than the body mass predicted for the large adult African elephant on display at Oxford University Museum of Natural history; 6209 kg. Sadly the accuracy of later prediction cannot be confirmed as no records remain of the body mass of this particular specimen. However, the value of 8500 kg is in very close agreement with the recent estimates of Woolly Mammoth body mass derived at using volumetric methods (8241 kg) [13]. What can be concluded, however, is that body mass prediction varies greatly with the type of equation selected and appears also to be speciesspecific in the case of some often used equations. In this study, the most accurate predictor of body mass was found to be equation 6, which combined both length and diameter parameters of the bone.
Concluding Issues
This study, which is the first to explore the relation between first rib parameters and body mass has important implications for furthering our understanding of basic biology, physiology and scaling, as well as potential applications in terms of estimating the body mass of extinct species as well as in the field of forensic science.
Acknowledgments
The authors are indebted to Birgitte Holle, Lennart Engberg Carlsen, Vibeke Bøgelund Hansen, Jan Henrik Woller and Dr Jan Odderskov Martin, Faculty of Health & Medical Sciences, Copenhagen University, for their kind help and assistance with the specimens, and very grateful to the staff of Copenhagen Zoo for allowing access to the rhinoceros and elephant skeletons in their possession, as well as the owner, Dr Frank Vigh Larsen, of the Scandinavian Animal Park, Djursland for granting access to ”Manse” their Woolly Mammoth skeleton. The authors also wish to thank Kole Carter and North Sea Fossils for supplying the Woolly Mammoth first rib and tibia fossils, respectively. Finally, thanks are due to Dr Malgosia Nowak-Kemp, Vertebrate Collection Manager, Oxford University Museum of Natural History for facilitating measurements of the Asian and African Elephants in the collection.
References
- Schmidt-Nielsen K (1984) Scaling – Why is animal size so important? Cambridge University Press, Cambridge
- Germonpré M, Sablin M, Khlopachev GA, Grigorieva GV (2008) Possible evidence of mammoth hunting during the Epigravettian at Yudinovo, Russian Plain. J Anthropological Archaeology 27(4): 475-492.
- Germonpré M (2003) Mammoth taphonomy of two fluvial sites from the Flemish Valley, Belgium. In: Reumer JWF, De Vos J, Mol D (Eds). Advances in Mammoth Research Deinsea 9: 171-184.
- Laws RM, Parker ISC, Johnstone RCB (1975) Elephants and their habitat: the ecology of Elephants in North Bynioro, Uganda.
- Christiansen P (2004) Body size in proboscideans, with notes on elephant metabolism. Zoological Journal of the Linnean Society 140: 523-549.
- Mol D, Shoshani JH, Tikhonov A, Geel B van, Sano S, et al. (2006) The Yukagir Mammoth: Brief history, 14C dates, individual age, gender, size, physical and environmental conditions and storage. Scientific Annals Special 98: 299-314.
- Forrest JB (1970) The effect of changes in lung volume on the size and shape of alveoli. J Physiol 210: 533-547.
- Kleiber M (1932) Body size and metabolism. Hildgardia 6: 315-353.
- Gehr P, Erni H (1980) Morphometric estimation of pulmonary diffusion capacity in two horse lungs. Respir Physiol 41: 199 210.
- Weibel ER (1979) Oxygen demand and the size of respiratory structures in mammals. In: Evolution of Respiratory Processes: A Comparative Approach. New York and Basel, Marcel Dekker Inc 13: 289-346.
- Cook CD, Helliesen PJ, Agathon S (1958) Relation between mechanics of respiration, lung size and body size from birth to young adulthood. J Appl Physiol 13(3): 349-352.
- Ruff CB (2003) Growth in bone strength, body size, and muscle size in a juvenile longitudinal sample. Bone 33: 317-329.
- Larramendi A (2016) Shoulder height, body mass, and shape of proboscideans. Acta Palaeontologica Polonica 61(3): 537-574.
- McMahon T (1975) Allometry and biomechanics: limb bones in adult ungulates. Amer Nat 109: 547-563.
- Biewener AA (1982) Bone strength in small mammals and bipedal birds: Do safety factors change with body size? J Exp Biol 98: 289-301.
- Galilei G (1637) Dialogues Concerning Two New Sciences – Translated by H Crew & A DeSalvio. New York, USA.
- Stahl WR (1965) Organ weights in primates and other mammals. Science 150(3699): 1039-1042.
- Stahl WR (1967) Scaling of respiratory variables in mammals. J Appl Physiol 22: 453-460.


 We use cookies to ensure you get the best experience on our website.
We use cookies to ensure you get the best experience on our website.