Chitosan Copolymer with Activated Carbon as Nanocomposite Through DFT Modeling

Abstract

Our aim is to simulate nanocomposites through intermolecular interactions among copolymer chitosan (Ch) and activated carbon (AC) in the simplest form of them. Structural properties as pore size distribution are to be investigated in this way. A geometry optimization (DMol3- DFT-GGA-PW91) among C₁₇ carbon-ring and a chitosan copolymer unit provides one nanocomposite system. First, we draw sketches of chitosan copolymer and arbitrary carbon rings to determine their structure stabilities through the minimum energy criterion, which is also applied on AC+Ch system. Second, we consider Cn carbon rings as activated carbon by knowing that average pore size distribution is around (9Å) according to BET measurements. Some carbon rings known as carbyne, alternate single and triple bonds, and those known as cumulene only have double bonds. The alternation of bond lengths in carbon rings is at least one signal of the consequences of Jahn-Teller effect. Third, we propose pore size distributions of the nanocomposite by means of radial distribution functions. Nanocomposite AC+Ch molecular complex system is expected to be applied in medicine as mitigating intoxication in human beings.

Introduction

With the aim to figure out a molecular complex formed through the interaction between a copolymer unit of chitosan and an activated carbon system arranged in planar ring way, adsorption energy has been calculated by means of minimum energy calculations obtained through DMol3 geometry optimization. Chitin is the second most abundant biopolymer in nature. When the degree of deacetylation of chitin reaches about 50% (depending on the origin of the polymer), it becomes soluble in aqueous acidic media and is called chitosan [1]. Chitosan is applied to remediation of heavy metals in drinking water and other contaminants by adsorption, because chitosan is macropore size [2] for long linear chains sets forming aggregates. In industrial applications, several solids having pores close to molecular dimensions (micropores < 20 Å) are used as selective adsorbents because of the physicochemical specificity they display towards certain molecules in contrast to the mesoporous substrates (20-500 Å) and macropores (> 500 Å) [3]. Adsorbents with these selective properties include activated carbon among others [4]. According to the micropore size distributions (MPSD), the most populated results for measurements of pore size of activated carbon is located around 9 Å, at the interval 6 - 18 angstroms in the pore size distribution [5].

There is a great variety of applications of activated carbon as an adsorbent material, and it has been used in areas related to the energy, and the environment, generating materials with a high-energy storage capacity [6]. Matrix isolation measurements [7] exhibit that carbon vapor at 3000K consists of atomic and molecular carbon of the approximate composition C (20%), C₂ (10%), and linear C₃ (70%); the abundance of larger species is rather low (<1%) [8]. Wakabayashi and Krätschmer remark that all odd chains have a closed-shell electronic structure in their ground state (i.e. are singlet states) and that all even chains have just two electrons in a π orbital which can host four electrons (i.e. possess a triplet ground state). When copper acetylide or dicopper acetylide are hydrolyzed with hydrochloric acid, they release polyenes in an extracting hydrocarbon medium and a carbonaceous residue containing carbenoid structures [9]. Structures of acetylenic-ring (carbenoid), and cumulenic-rings have been obtained through Montecarlo [10] and DFT geometry optimization [11]. According to Remya (2016) and references there in, properties of planar monocyclic carbon rings have been extensively studied both theoretically and experimentally.

These properties vary with the number n of carbon atoms, depending on whether n is odd, n=4N, or n=4N+2 where N is an integer. Linear carbons alternating single and triple bonds (-C≡C-)_n, are known as carbine or acetylenic structures, while when double bonds are present (═C═C═)_n (Liu 2013) the structure is known as cumulene. Polyyne is known as an allotrope carbon having H(-C≡C-)_nH chemical structure repeating chain, with alternating single and triple bonds [12] and hydrogen at every extremity, corresponding to hydrogenated linear carbon chain as any member of the polyyne family HC_2nH [13] with sp hybridization atoms. It is known that polyyne, carbyne, carbynoid, cumulene and cumulenic have been actually synthesized as documented by Cataldo [14]. Bond length alternation (BLA) of carbyne pattern is retained in the rings having an even number of atoms [15]. Additional care must be taken with carbyne rings since the Jahn–Teller distortion (the counterpart of Peierls instability in non-linear molecules) is different in the C_4N and C_4N+2 families of rings [10, 16,17].

Particularly, nanostructures of planar monocyclic carbon rings C_n with n = 4N +2, where N is a natural number, are closed-shell molecules revealing an intriguing competition between conjugated aromaticity, second-order Jahn-Teller [18] and, at large sizes, Peierls instability effects. Consequently, this leads to different stabilization mechanisms that tend to favor one of three following structures: i) a cumulenic ring with full Dnh symmetry, with all bond angles and bond lengths equal; or either of two distorted acetylenic ring structures, of lower D(n/2)h symmetry, with alternating ii) bond angles or iii) bond lengths (Torelli 2000). Methods of synthesis of large monocyclic ring structures (n<30) [19] and of experimentally isolating specific size clusters [20] provide relatively precise spectral information for neutral carbon rings as a function of size [21]. These results suggest that aromatic behavior (no bond alternation for n=4N+2 rings, where N is a natural number) is retained for molecules larger than previously predicted by Hartree-Fock [22] (HF) and accepted in structural chemistry.

Intermolecular carbon-carbon interactions and stability have been investigated on C_4N and C_4N+2, carbon ring systems for N=1, … , 7 except C_4N when N=1 using DFT-mGGA-M-06l level of theory with the basis set 6-311++g(d,p) [11]. The properties of these rings vary with the number n of carbon atoms, depending on whether n is odd, n=4N or n=4N+2. The C_4N+2 rings show cumulenic structures with all the bond lengths being equal, while the C_4N rings possess carbyne type structures with clear bond length alternation. In principle, electronic structure of diatomic molecules has been built through the overlapping knowledge of the interacting atomic orbitals [23]. In this case, the orbitals correspond to bonding (σ_g, π_g) and antibonding (σ_u, π_u) orbitals of hydrogen, carbon, nitrogen and oxygen diatomic molecules, whose H₂, C₂, N₂, and O₂ ground-state electronic configurations are 1σ_g² , 1σ_g²1σ_u² 1Π_u4 , 1σ_g²1σ_u²1Π_u42σ_g² and 1σ_g²1σ_u²2σ_g²1Π_u41Π_g4 with 2, 8, 10 and 12 valence electrons, respectively. Actually, the reactivity sites in a molecule correspond to the highest occupied molecular orbitals (HOMO) and lowest unoccupied molecular orbitals (LUMO). HOMO as base (donor), and LUMO as acid (acceptor) are particularly important MOs to predict reactivity in many types of reaction [24,25].

Particularly, nanostructures of planar monocyclic carbon rings C_n with n = 4N +2, where N is a natural number, are closed-shell molecules revealing an intriguing competition between conjugated aromaticity, second-order Jahn-Teller [18] and, at large sizes, Peierls instability effects. Consequently, this leads to different stabilization mechanisms that tend to favor one of three following structures: i) a cumulenic ring with full Dnh symmetry, with all bond angles and bond lengths equal; or either of two distorted acetylenic ring structures, of lower D(n/2)h symmetry, with alternating ii) bond angles or iii) bond lengths (Torelli 2000). Methods of synthesis of large monocyclic ring structures (n<30) [19] and of experimentally isolating specific size clusters [20] provide relatively precise spectral information for neutral carbon rings as a function of size [21]. These results suggest that aromatic behavior (no bond alternation for n=4N+2 rings, where N is a natural number) is retained for molecules larger than previously predicted by Hartree-Fock [22] (HF) and accepted in structural chemistry.

Intermolecular carbon-carbon interactions and stability have been investigated on C_4N and C_4N+2, carbon ring systems for N=1, … , 7 except C_4N when N=1 using DFT-mGGA-M-06l level of theory with the basis set 6-311++g(d,p) [11]. The properties of these rings vary with the number n of carbon atoms, depending on whether n is odd, n=4N or n=4N+2. The C_4N+2 rings show cumulenic structures with all the bond lengths being equal, while the C_4N rings possess carbyne type structures with clear bond length alternation.In principle, electronic structure of diatomic molecules has been built through the overlapping knowledge of the interacting atomic orbitals [23]. In this case, the orbitals correspond to bonding (σ_g, π_g) and antibonding (σ_u, π_u) orbitals of hydrogen, carbon, nitrogen and oxygen diatomic molecules, whose H₂, C₂, N₂, and O₂ ground-state electronic configurations are , , and  with 2, 8, 10 and 12 valence electrons, respectively. Actually, the reactivity sites in a molecule correspond to the highest occupied molecular orbitals (HOMO) and lowest unoccupied molecular orbitals (LUMO). HOMO as base (donor), and LUMO as acid (acceptor) are particularly important MOs to predict reactivity in many types of reaction [24,25].

In interaction studies of graphene-chitosan [26,27], one monomer of chitosan (MCh) unit stays almost perpendicularly adsorbed on a C₅₄H₁₈ graphene (G) sheet in T-shape form. DFT-mGGA-M06L was applied to deal with the exchange–correlation energies using all-electron basis set with triple polarization. The minimum energy criterion was applied for determining the structure stability on the G + MCh system using seven different geometries; in addition, they checked with the non-complex vibration frequency. On the other hand, studies of adsorption of chitosan on (5,5) and (5,0) BN nanotubes also exhibit chitosan perpendicularly adsorbed to the latter [28]. In this case they applied DFT-LDA, and the exchange-correlation term was modeled with the Perdew-Wang parameterization. The structural stability was based on finding the minimum energy and non-complex vibrational frequencies. Different sites, charge (neutral, cation and anion) and orientations of chitosan, using the monomer unit, were considered. For the (5,5) nanotube, the minimum energy site corresponds to that one when the monomer (for all charges assigned) is perpendicular to the nanotube; only structural stability was found in the anion assignment for the (5,0) nanotube.

Structures of Acetylenic- and cumulenic- rings are obtained from irregular carbon rings. We consider these structures as carbon physically activated, due to the pore size distribution, and since no activating chemical agent has been applied. Activated carbon and chitosan have been independently applied as adsorption materials to increase environmental quality starndards. Then, we expect AC-Ch nanocomposite to have a powerful adsorption property of pollutants that can be applied not only in wastewater treatment, but also in medicine against intoxication, according to the pore size distribution generated on this new material.

Methodology

The interaction between an activated carbon system (AC) and a unit of chitosan copolymer (Ch) is studied by means of BIOVIA Materials Studio software DFT-DMol³ [29,30]. The AC system is cumulenic- or acetylenic- ring of double bonds or single-triple bonds, respectively. An even C_n carbon atoms number includes n=4N+2 for N=1,2,3…, which has been considered cumulenic-ring; however, it is acetylenic-ring when the symmetry is D_(n/2)h [10]. To obtain the minimum energy each ring is previously optimized by using DFT and converges into a planar molecular carbon ring structure when the symmetry is n=4N or N=4N+2. The reactants are AC + Ch, as an example: C₁₇ + C₁₄H₂₄N₂O₉, with C₃₁H₂₄N₂O₉ product as a new nanocomposite material. All electron calculations to find interaction energies among reactants AC+Ch (Activated Carbon + Chitosan) on DMol³ with GGA-PW91 functional [31-35], unrestricted spin, and dnd bases have been accomplished. Connectivity calculations [36] in an few cases where the bond remained very long after geometry optimization were accomplished in our nanocomposite mostly composed of carbon for bond length tolerances from 0.6 to 1.15 Å, according to DMol³ on no-bonding to s- and f-shell scheme bond type, and converting representation to Kekulé.

Radial Distribution Functions (RDF - BIOVIA Materials Studio) were calculated after building a periodic cell (Amorphous Cell - BIOVIA Materials Studio) using 1 gr/cc as density for one unit at room temperature, with universal forcefield to observe the distribution of atom distances. RDF is in here considered as something near to the pore size distribution in some manner. Origin software is used for linear regressions of nine-degree polynomial fitting connected by a B-Spline. These calculations have been achieved on RDFs of one thousand points, providing an approximate area of 20 Ų, and recalculated in each case. Energy calculated by means of geometry optimization on each molecular system allows to obtain adsorption energy through the equation: E_ad(chAC)=E_(ch+AC)-E_(ch)-E_(AC)(1)

Results

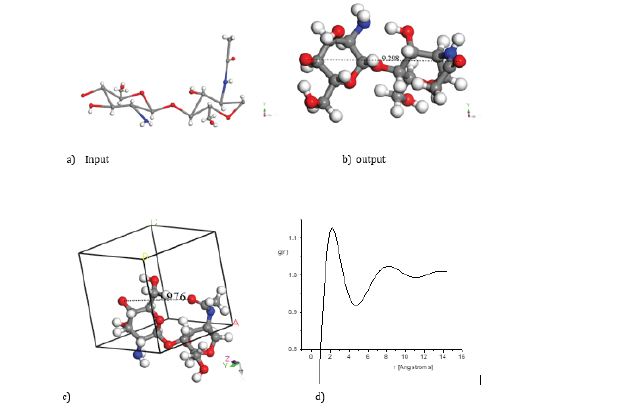
Figure 1: Geometry optimization applied to Chitosan copolymer with molecular structure C₁₄H₂₄N₂O₉: a) Input (drawing the chitosan system). b) Output (optimized geometry of this system). c) Periodic cell for this system. d) Radial distribution system in this case. Atoms of: Hydrogen in white color, Nitrogen in blue color, Oxygen in red color and Carbon in gray color.

An input-output chitosan copolymer is observed in Figure 1. The output is a molecular structure resulting after calculating the minimum energy E_(ch)= −5114.7 kcal/mol through DMol3 DFT-GGAdnd geometry optimization. Considering the whole surface area of the latter molecular unit in Figure 1b, an average micropore size diameter of 9.298 Å is estimated in agreement with micropore size distributions [37]. This diameter estimation also agrees with the corresponding radial distribution function, because each maximum is located as a distribution of atom distances, and we clearly observe two maximums, one at 2.20 Å and another at 8.18 Å; however, there is another small maximum around 13.7 Å. The first maximum is an average distance very close to the nearest atom neighbours, which is near to the atom bond lenght, the second one provides an average distance from those atoms not so near not so far, and the third maximum give information about the average distance of the far away atoms, the rest atoms do not feel the presence of each other.

The C₁₇ cumulenic-ring double bond among carbons is obtained as shown in Figure 2 by applying DFT geometry optimization and bond type to an irregular system of seventeen single bond carbons, the optimized energy obtained is E(c₁₇) 2653.01 kcal/mol. D_17h symmetry on an odd carbon number for monocycle C₁₇ carbon-ring molecular structure is shown in Figure 2a, when alternating long/ short bond lengths are present, as a clear evidence of Jahn-Teller effect due to there is no perfect symmetry. In a perfect symmetry there is equal bond lengths and angles as it is observed in Figure 2b. In the previous cases when n is even carbon number the D_nh symmetry is circular while D_(n/2)h symmetry is a polyhedron. When n is odd Dnh exhibits two cases: i) alternating bond lengths showing Jahn Teller effect, and ii) equal bond lengths and angles. The RDF was obtained after building a periodic cell for C₁₇-cumulenic-ring as seen in Figure 2c. Peaks of the radial distribution function are located at 1.89 Å, 6.26 Å, and 12.36 Å, according to Figure 2d.

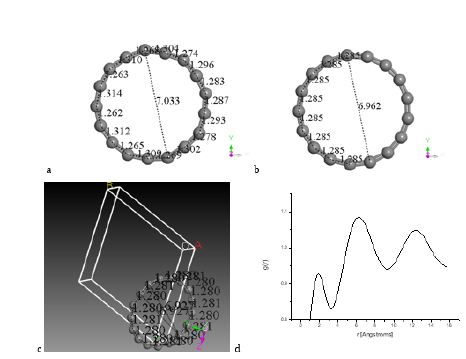
Figure 2: In a D_17h symmetry of C₁₇-cumulenic ring structure: a) Jahn Teller effect is clearly observed due to alternating bond lengths with area 38.84 Ų, b) equal bond lengths and angles with ring area 37.61 Ų, c) periodic cell for C₁₇-cumulenic-ring, d) Radial distribution function applied to C₁₇ ring in a periodic cell.

In case of Figure 3, we consider input-output geometry optimization when we join C₁₇-cumulenic ring with chitosan C₁₄H₂₄N₂O₉ as in Figure 3a-b, and each one previously at its minimum energy. Then, we applied geometry optimization to the whole system obtaining E_ad(chAC) = −6811.5 kcal/mol. We also considered bond type criteria and Kekulé representation as shown in Figure 3c. This result is a good example of the possibility of modifying the pore size distribution of chitosan when it is embedded into activated carbon. In order to have a normalized RDF, the nanocomposite is introduced in a periodic cell shown in Figure 3d, and the radial distribution function is shown in Figure 3e where peaks are located at 2.09 Å, 8.09 Å, and 13.70 Å. The product in the output (Figure 3c) is the nanocomposite C₃₁H₂₄N₂O₉, and we also applied bond type criteria to observe a change of double bonds to single and triple bonds. The adsorption energy in this case is E_ad = −6811.5+5114.7+2653.01=956.3 kcal/mol according to Equation 1, which corresponds to chemisorption energy agreeing to the range handled by Atkins [38,39].

Figure 3: Here we consider input-output geometry optimization: a) Input of a C₁₇-cumulene ring surrounding a chitosan copolymer molecule. b) Output of the previous CA-Chitosan, now as nanocomposite. c) Connectivity criteria applied to nanocomposite. d) This nanocomposite into periodic boundary conditions. e) The radial distribution functions.

Figure 3: Here we consider another input-output geometry optimization of one C₁₇-cumulenic ring with one chitosan copolymer molecule: a) Input of the reactants in face to face orientation, b) Output of the product in T-shape orientation, now as nanocomposite, c) C₁₇-cumulenic-ring outside the box of periodic boundary conditions, and d) its corresponding RDF, e) C₁₇-cumulenic-ring inside the box, and f) its corresponding RDF.

The C₁₇-cumulenic ring structure surrounding a chitosan copolymer molecule has been optimized in three dimensions using DMol3, in which we clearly observe parts of curved carbon chains passing from double bonds to single and triple bonds. This new nanocomposite has a pore size distribution different to those of the previous C₁₇-cumulenic ring structure alone, or the chitosan C14H44N2O9 copolymer molecule. We considered another configuration moving C₁₇-cumulenic ring in Figure 3a towards face to face orientation as in Figure 4a. We applied minimum energy using DMol3 geometry optimization and the result is shown in Figure 4b. The C₁₇-cumulenic ring started parallel to the chitosan copolymer and ended perpendicular to it. According to the initial orientation, the T-shape obtained in the nanocomposite product is due to a repulsion on cumulenic carbon atoms in the ring applied by chitosan copolymer, while one carbon of this C₁₇-cumulenic ring inserts one OH bond of Chitosan copolymer. The optimized energy obtained is E_(ch+cg)= −7786.709 kcal/mol. In this case, two periodic cells showing different geometry orientations were built, see Figures 4c and 4e. Peaks of the radial distribution function in Figure 4d are located at 2.37 Å, 7.44 Å, and 13.04 Å; while in Figure 4f are at 2.21 Å, 7.31 Å, and 12.87 Å. The adsorption energy in this case is E_(ad) =−7786.709+5114.7+2653.01 _18.99 = kcal/mol. The absolute value of this result corresponds to the bond strength of a well of potential, which is an almost physisorption or a very weak chemisorption. In this case the separation of the cumulenic-ring from chitosan copolymer is easier than in the previous case. Then, it is considered that the properties of the reactants are still almost invariants.

Discussion

Different elongation among single and triple carbon bond lengths in carbynoid-rings, or double bonds in cumulenic-rings, are due to Jahn-Teller effect (Bylaska 1998). Then, when C₁₇ cumulenic- ring is optimized, the alternating angles or bond lengths are due to quantum distortion effect. The Jahn-Teller effect is also present in C₁₂ carbynoid-ring, or in C_4N carbynoid-rings, generally. Carbon rings C_4N (N<~8) exhibit a substantial first order Jahn-Teller distortion that leads to long/short (single/triple) bond alternation decreasing with increasing N [16]. The carbon model chosen is among allotropes, from which the most known are fullerenes, nanotubes and graphite; less known is zeolite templated carbon as an example. Polyyne and cumulene are more allotrope forms not so known among many investigators in research community, because they still think these are hypothetical; however, synthesis of them have been accomplished. Again, after practicing connectivity [36], bond type, and Kekulé representation, we infer that bonding type change produced the differences, and the correct values correspond to the correct bonding type in the new molecular complex system formed.

We consider each carbon ring as physically activated through geometry optimization, due to pore size diameter remains in the average size compared against experimental measurements [40]. The optimized C₁₇ carbon-ring system and one optimized chitosan copolymer unit have been studied by considering the result after the corresponding geometry optimization, as a molecular complex obtained when they were joined to form what is also nanocomposite called. In a previous work [41,42], an almost T-shape form between one chitosan copolymer unit and one C₉-cumulenic-ring was obtained, where C₉-cumulenic-ring was not initially flat after geometry optimization was applied, and consequently with partial aromaticity. In this case, our C₁₇-cumulenic-ring is flat increasing in this way its aromaticity. This might be one reason to obtain an increased perpendicularity between chitosan copolymer unit and C₁₇-cumulenic-ring. Another reason might be its degeneracy due to Jahn-Teller effect [18], because high degeneracy indicates high symmetry of the molecule, consequently the system tends to be distorted, in such way that when moving, the occupied levels are down and the unoccupied ones are up [26].

Our result of a nanocomposite formed with chitosan copolymer T-shape with C₁₇-cumulenic-ring agree with the results presented by Chigo et al. in a study of the interaction among graphene-chitosan for a relaxed system doped with boron, in which they consider the interaction of pristine graphene with the monomer of chitosan (G + MCh: C₆H₁₃O₅N ) in different configurations, whereas we consider relaxed chitosan copolymer C₁₄H₂₄N₂O₉ with C₁₇ cumulenic-ring. While Chigo et al. found a perpendicular chitosan molecule linked to a carbon nanotube system, we obtained a C₁₇ cumulenic-carbon ring perpendicularly linked to a chitosan copolymer system.

Funding Acknowledgement

This work was supported by Tecnológico Nacional de México [grant number TOL-PYR-2016-078].

References

• Rinaudo M (2006) Chitin and chitosan: properties and applications. Prog Polym Sci 31: 603-632.
• Khang G (2012) Handbook of Intelligent Scaffold for Tissue Engineering and Regenerative Medicine. CRC Press, Taylor and Francis, Boca Ratón, FL.
• Cardona V (2012) (Spanish) Physicochemical and structural preparation and characterization of a chitosan-based conducting gel. BSc Degree, Universidad del Valle, Santiago de Cali, Colombia.
• Wang CM, Chang KS, Chung TW, Wu H (2004) Adsorption equilibria of aromatic compounds on activated carbon, silica gel, and 13x zeolite. J Chem Eng Data 49: 527-531.
• Lozano D, Cazorla D, Linares A (2002) Powdered Activated Carbons and Activated Carbon Fibers for Methane Storage: A Comparative Study. Energy & Fuels 16: 1321-1328.
• Smisek M, Cerny S (1970) Active carbon: manufacture, properties and applications. Elsevier, New York.
• Wakabayashi T, Krätschmer W (2006) Carbon chain molecules in cryogenic matrices. In: Cataldo F (ed) Polyynes: Synthesis, Properties, and Applications. CRC Taylor and Francis: Boca Raton, FL, pp: 99-125.
• Zavitsanos PD, Carlson GA (1973) Experimental study of the sublimation of graphite at high temperatures J Chem Phys 59: 2966.
• Cataldo F (ed) (2006) Polyynes: Synthesis, Properties, and Applications. CRC Taylor and Francis: Boca Raton, FL.
• Torelli T, Mitas L (2000) Electron Correlation in C4N+2 Carbon Rings: Aromatic Versus Dimerized Structures. Phys Rev Lett 85: 1702–1705.
• Remya K, Suresh CH (2016) Carbon rings: Study of geometry, aromaticity, intermolecular carbon-carbon interactions and stability. RSC Adv 6(50): 44261-44271.
• Baughmann RH (2006) Dangerously Seeking Linear Carbon. Science 312: 1009-1110.
• Ding H, Schmidt TW, Pino T, Güthe F, Maier JP (2003) Towards bulk behavior of long hydrogenated carbon chains? Phys Chem Chem Phys 5: 4772.
• Cataldo F, Keheyan Y (2006) Polyynes: Simple synthesis in solution through the glaser reaction. In: Cataldo F (ed) Polyynes: Synthesis, Properties, and Applications. CRC Taylor and Francis: Boca Raton, FL, pp: 493- 498
• Liu M, Artyukhov VI, Lee H, Xu F, Yakobson BI (2013) Carbyne from First Principles: Chain of C Atoms, a Nanorod or a Nanorope. ACS Nano,
• Bylaska EJ, Weare JH, Kawai R (1998) Development of Bond-Length Alternation in Very Large Carbon Rings: LDA Pseudopotential Results. Phys Rev B 58: R7488–R7491.
• Saito M, Okamoto Y (1999) Second Order Jahn–Teller Effect on Carbon 4N+2 Member Ring Clusters. Phys. Rev. B 60: 8939–8942.
• Jahn HA, Teller E (1937) Stability of Polyatomic Molecules in Degenerate Electronic States. I. Orbital Degeneracy. Proc R Soc London A 161: 220- 235.
• Rubin Y, Kahr M et al (1991) The higher oxides of carbon C8nO2n (n = 3-5): synthesis, characterization, and x-ray crystal structure. Formation of cyclo[n]carbon ions Cn+ (n = 18, 24), Cn- (n = 18, 24, 30), and higher carbon ions including C60+ in laser desorption Fourier transform mass spectrometric experiments. J Am Chem Soc 113: 495.
• Handschuh H, Ganteför G, Kessler B, bechthold PS, Eberhardt W (1995) Stable Configurations of Carbon Clusters: Chains, Rings, and Fullerenes. Phys Rev Lett 74: 1095-1098.
• Wakabayashi T et al (1997) Photoelectron spectroscopy of Cn produced from laser ablated dehydroannulene derivatives having carbon ring size of n = 12, 16, 18, 20, and 24 J Chem Phys 107: 4783.
• Martin JML, El-Yazal J, François JP (1995) Structure and vibrational spectra of carbon clusters C n ( n = 2-10, 12, 14, 16, 18) using density functional theory including exact exchange contributions. Chem Phys Lett 242: 570-579.
• Atkins P, Friedman R (2005) Molecular Quantum Mechanics. 4th edn. Oxford University Press, New York.
• Fukui K, Yonezawa T, Nagata C, Shingu H (1954) Molecular orbital theory of orientation in aromatic, heteroaromatic, and other conjugated molecules. J Chem Phys 22: 1433-1442.
• Lewis G (1923) Valence and the Structure of Atoms and Molecule. The Chemical Catalog Company, inc.
• Chigo E, Torres A, Hernández H (2014) Studies of graphene–chitosan interactions and analysis of the bioadsorption of glucose and cholesterol. Appl Nanosci 4: 911–918.
• Kadokawa JI (2014) Preparation of Chitin-Based Nano-Fibrous and Composite Materials Using Ionic Liquids. In: Han-Chan C, Hua-Chia C, Thomas S (ed) Physical Chemistry of Macromolecules: Macro to Nanoscales, CRC Press, Apple Academic Press, New Jersey, pp 367-384
• Rodriguez A, Chigo E, Hernandez H, Flores A (2013) Adsorption of chitosan on BN nanotubes: A DFT investigation. Appl Surf Sci 268: 259– 264.
• Delley B (1995) DMol, a standard tool for density functional calculations; review and advances. In: Seminario JM, Politzer P (eds) Modern density functional theory: a tool for chemistry. Elsevier, Amsterdam, pp: 221-254.
• Auckenthaler T, Blum V, Bungartz HJ, Huckle T, Johanni R, et al. (2011) Parallel solution of partial symmetric eigenvalue problems from electronic structure calculations. Parallel Computing 37: 783.
• Delley B (1990) An all‐electron numerical method for solving the local density functional for polyatomic molecules. J Chem Phys 92: 508.
• Delley B (2000) From molecules to solids with the DMol3 approach. J Chem Phys 113: 7756-7764.
• Perdew JP, Wang Y (1986) Accurate and simple density functional for the electronic xchange energy: Generalized gradient approximation. Phys Rev B 33: 8800-8802.
• Perdew JP (1991) Generalized gradient approximations for exchange and correlation: A look backward and forward. Physica B 172:1-6.
• Perdew JP, Wang Y (1992) Accurate and simple analytic representation of the electron-gas correlation energy. Phys Rev B 45:13244-13249.
• Estrada E (2002) Physicochemical Interpretation of Molecular Connectivity Indices. J Phys Chem A 106: 9085-9091.
• Pacheco JH, Zaragoza IP, Bravo A (2017) Interaction of small carbon molecules and zinc dichloride: DFT study. Rev Mex Fís 63: 97–110.
• Atkins P, De Paula J (2010) Physical Chemistry. Freeman and Company, New York.
• Guibal E, Milot C, Tobin J (1998) Metal-anion sorption by chitosan beads: equilibrium and kinetic studies. Ind Eng Chem Res 37:1454-1463.
• Isidro FJ, Pacheco JH, Desales LA (2017) Hydrogen Storage on lithium decorated zeolite templated carbon, DFT study. International Journal of Hydrogen Energy.
• Hernández-Benitez D, Pacheco-Sánchez JH (2018) Optimization of Chitosan+ Activated Carbon Nanocomposite. DFT Srudy. Arc Org Inorg Chem Sci 3(5): 436.
• Sakurai K, Maegawa T, Takahashi T (2000) Glass transition temperature of chitosan and miscibility of chitosan/poly(N-vinyl pyrrolidone) blends. Polymer 41: 7051–7056.
• Suvachittanont W, Kurashima Y, Esumi H, Tsuda M (1996) Formation of thiazolidine-4-carboxylic acid (thioproline), an effective nitrite-trapping agent in human body, in Parkia speciosa seeds and other edible leguminous seeds in Thailand. Food Chem 55(4): 359-363.
• Tunsaringkarn T, Suwansaksri J, Rungsiyothin A, Palasuwan A (2014) Cell proliferation activities in vitro model of Thai mimosaceous extracts. J Chem Pharm Res 6(1): 507-511.
• Tsuda M, Kurashima Y (1991) Nitrite-trapping Capacity of Thioproline in The Human Body. IARC Sci Publ 105: 123-128.
• Nakatogawa H and Ohsumi Y (2008) Starved cells eat ribosomes. Nat Cell Biol 10: 505- 507.
• Uyub AM, Nwachukwu IN, Azlan AA and Fariza SS (2010) In vitro antibacterial activity and cytotoxicity of selected medicinal plant extracts from Penang island Malaysia on metronidazole resistant Helicobacter pylori and some pathogenic bacteria. Ethnobotany Research and Applications 8: 95-106.
• Sakunpak A, Panichayupakaranant P (2012) Antibacterial activity of Thai edible plants against gastrointestinal pathogenic bacteria and isolation of a new broad spectrum antibacterial polyisoprenylated benzophenone, chamuangone. Food Chem 130(4): 826-831.
• Gmelin R, Susilo R, Fenwick GR (1981) Cyclic polysulphides from Parkia speciosa. Phytochemistry 20(11): 2521-2523.
• Musa N, Wei LS, Seng CT, Wee W, Leong LK (2008) Potential of Edible Plants as Remedies of Systemic Bacterial Disease Infection in Cultured Fish. Glob J Pharmacol 2(2): 31-36.
• Randhir R, Ms YL, Shetty K (2004) Phenolics, their antioxidant and antimicrobial activity in dark germinated fenugreek sprouts in response to peptide and phytochemical elicitors. Asia Pac J Clin Nutr 13(4): 295-307.
• Wonghirundecha S, Sumpavapol P (2012)Antibacterial Activity of Selected Plant By-products Against Food- borne Pathogenic Bacteria. Int Conf Nutr Food Sci 39(1): 116-20.
• Thitilertdecha N, Teerawutgulrag A, Rakariyatham N (2008) Antioxidant and antibacterial activities of Nephelium lappaceum L. extracts. LWT - Food Sci Technol 41(10): 2029-2035.
• Suklampoo L, Thawai C, Weethong R, Champathong W, Wongwongsee W (2014) Antimicrobial Activities of Crude Extracts from Pomelo Peel of Khao-nahm-peung and Khao-paen Varieties. KMITL Sci Technol J 12(1).
• Mokbel MS, Hashinaga F (2009) Antibacterial and Antioxidant Activities of Banana (Musa, AAA cv. Cavendish) Fruits Peel. Am J Biochem Biotechnol1( 3): 125-131.
• Fatimah I (2016) Green synthesis of silver nanoparticles using extract of Parkia speciosa Hassk pods assisted by microwave irradiation. J Adv Res 7(6): 961-969.
• Mustafa NH, Ugusman A, Jalil J, Kamisah Y (2018) Anti-inflammatory property of Parkia speciosa empty pod extract in human umbilical vein endothelial cells. J Appl Pharm Sci 8(1): 152-158.
• Gui JS, Jalil J, Jubri Z, Kamisah Y (2019) Parkia speciosa empty pod extract exerts anti-inflammatory properties by modulating NFκB and MAPK pathways in cardiomyocytes exposed to tumor necrosis factor-α. Cytotechnology 71(1): 79-89.
• Kamisah Y, Zuhair JSF, Juliana AH, Jaarin K (2017) Parkia speciosa empty pod prevents hypertension and cardiac damage in rats given N(G)-nitro- L-arginine methyl ester. Biomed Pharmacother 96(8): 291-298.
• Karunaweera N, Raju R, Gyengesi E (2015) Plant polyphenols as inhibitors of NF-κB induced cytokine production- a potential anti-inflammatory treatment for Alzheimer’s disease? Front Mol Neurosci 8(6): 1-5.
• Sorriento D, Santulli G, Fusco A, Anastasio A, Trimarco B, et al. (2010) Intracardiac injection of AdGRK5-NT reduces left ventricular hypertrophy by inhibiting NF-κB-Dependent hypertrophic gene expression. Hypertension 56(4) 696-704.
• Huang GJ, Huang SS, Deng JS (2012) Anti-inflammatory activities of inotilone from Phellinus linteus through the inhibition of MMP-9, NF-κB, and MAPK activation in vitro and in vivo. PLoS One 7(5).
• Martin ED, Felice De Nicola G, Marber MS (2012) New therapeutic targets in cardiology: P38 alpha mitogen-activated protein kinase for ischemic heart disease. Circulation 126(3): 357-368.
• Galindo P, Gonzalez-Manzano S, Zarzuelo MJ, Gomez-Guzman M, Quintela AM, et al. (2012) Different cardiovascular protective effects of quercetin administered orally or intraperitoneally in spontaneously hypertensive rats. Food Funct 3(6): 643-650.
• Huang WY, Fu L, Li CY, Xu LP, Zhang LX, et al. (2017) Quercetin, Hyperin, and Chlorogenic Acid Improve Endothelial Function by Antioxidant, Antiinflammatory, and ACE Inhibitory Effects. J Food Sci 82(5): 1239-1246.