Short Communication 
Creative Commons, CC-BY
Coulomb’s Law Stand to The World of Elementary Particles in the Way That Newton’s Laws of Classical Mechanics Stand to The Macroscopic World
*Corresponding author: Yin Yue Sha, Dong ling Engineering Center, Ningbo Institute of Technology, Zhejiang University, China.
Received: October 06, 2019; Published: October 31, 2019
DOI: 10.34297/AJBSR.2019.06.000989
Abstract
According to the Classical Electron Orbital Radius and the force equilibrium relation before the disintegration of the neutron, we can calculate the sharp radius of the neutron; According to the density of nucleus and the sharp radius of the neutron, we can calculate the sharp radius of the electron; According to the sharp radius of the electron and the force equilibrium relation that electron with the Critical Photon, we can calculate the sharp electron radius of the Critical Photon; From the density of nucleus, we can obtain the mass of the Critical Photon; From the light velocity, we can obtain the energy of the Critical Photon; From the Planck’s constant, we can obtain the frequency of the Critical Photon; From the light velocity, we can obtain the wavelength of the Critical Photon; We discover that the wavelength of the Critical Photon is in the peak position of the solar spectrum energy radiation. Coulomb’s law stand to the world of elementary particles in the way that Newton’s laws of classical mechanics stand to the macroscopic world.
Keywords: Neutron; Proton; Electron; Critical Photon; Mass; Radius; Frequency; Density
Introduction
One: The Disintegration of the Neutron
The neutron can spontaneously produce disintegration and turn into the proton, at the same time send out an electron and some matter. According to the force equilibrium relation, before the disintegration of the neutron, there was the formula as follows:
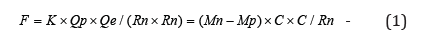
Where the K is the electromagnetic constant; the Qp is the electric charge of the proton; the Qe is the electric charge of the electron; the Mn is the mass of the neutron; the Mp is the mass of the proton; the Rn is the radius of the neutron; the C is the light velocity.
The total mass for releasing from neutron disintegration is Mn - Mp as follows:
where the Mn is the mass of the neutron, the Mp is the mass of the Proton and the Me is the mass of the electron.
Two: The Radius of the Neutron
From formula (1), we can acquire the calculation formula of the neutron radius,
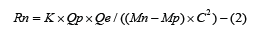
According to exact physical constants from modern science, we take the following values:
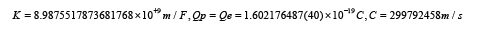
from formula (2), we can calculate the radius Rn of the neutron:
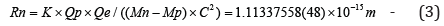
Three: The Frequency of the Neutron
From the radius of the neutron, we can compute the frequency of the neutron:
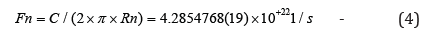
Four: The Density of the Neutron
From the radius of the neutron, we can compute its density:
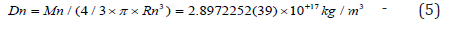
Five: The Radius of the Proton
According to the density of the neutron, we can calculate the radius of the proton:
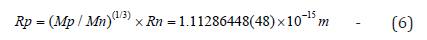
Six: The Radius of the Electron
According to the matter density of neutron, we can calculate the radius of Electron:
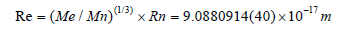
Seven: The Radius of the Atomic Nucleus
According to the radius of the neutron and the density of matter, we can calculate the radius of the atomic nucleus:
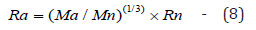
where the Ma is the mass of the atomic nucleus and Ra is the radius of atomic nucleus.
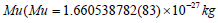is the atomic mass unit and Ru is its
radius.
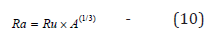
where the A is the nuclear number of the atomic nucleus
Eight: The Physical Constants of the Critical Photon
According to the radius of the electron and the density of the Neutron, we can calculate the mass of the Critical Photon and other Physical Constants:
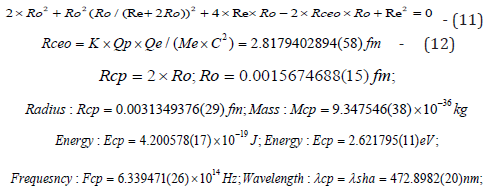
Apply the Wien’s law we can obtain:
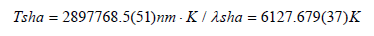
We use cookies to ensure you get the best experience on our website.