Prediction Based on Random Survival Forest

Abstract

Random survival forest (RSF) is an ensemble of survival trees where each tree within the forest is grown non-deterministically. RSF is an attractive nonparametric alternative in modeling time-to-event data when the number of covariates is larger than the number of subjects and the relationship between the response and covariates is complex. In this note, we discuss three main aspects in tree construction procedure in a nontechnical manner. Specifically, we review the node splitting rule, ways to construct right-sized trees to avoid overfitting and estimation in terminal nodes once the tree has grown to full size.

Keywords: Random Survival Forest; Right Censored Data; Survival Tree

Introduction

Collection of large number of clinical and genomic data for individuals are initiated with the hope of finding clinically significant diagnostic and prognostic factors for diseases. In studies involving progression in joint damage in psoriatic arthritis, for example, interests may lie in detecting HLA alleles associated with different disease courses [11]. Along with the genomic data in clinical cohort studies, it is common to have time-to-event end points resulting in right-censored data [2]. One of the objectives in these studies is to predict the future course of the disease at population or patient level based on covariate information.

Numerous parametric, semi-parametric and non-parametric methods have been developed in the literature. Cox proportional hazards model is well-establish and popular among those approaches for its flexibility and simplicity [3]. Several extensions have been implemented such as the penalized Cox and boosting in Cox regression to accommodate variable selection or prediction [2,4]. Random survival forest (RSF) is a non-parametric ensemble tree method which extends Brieman’s random forest to rightcensored data [5]. RSF serves as an attractive alternative in handling data consist of more covariates than subjects, complex and nonlinear relationships between response and covariates and when the proportionality hazard assumption may be at risk [6,7]. In this note we give an overview on RSF in a nontechnical manner. Specifically, we will discuss the three main aspects in tree-based estimation procedures in the next section, illustrate the method in real data example and end with a brief discussion.

Tree-Based Methods

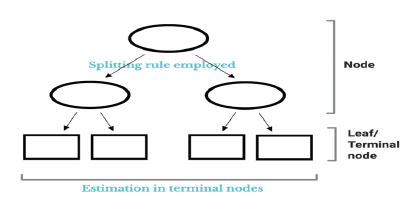
A tree is composed of numerous nodes as illustrated in (Figure 1). Tree estimation is in general based on recursively performing binary partitioning on the covariate space using some pre-defined splitting rule. The result is a collection of candidates ‘nodes’, starting from the top (single-node) of the tree to a number of terminal nodes or leafs [8]. RF is an ensemble of trees, hence the term forest, where the final prediction is averaged over all trees in the forest. Each tree is non-deterministic as the tree is grown on a subspace of individuals who were picked from bootstrapping the whole dataset [9]. Growing a single tree is well known to exhibit high variances in predicted outcomes. By combining the trees, however, variance as well as bias in prediction can be substantially decreased [10].

Figure 1:Simple representation on the composition of a tree.

There are three main aspects in tree-based estimation procedures, namely (1) the node splitting rule to partition the covariate space, (2) selection on the size of the tree to avoid overfitting and (3) estimation in the terminal nodes once the tree has grown to full size. Splitting is usually done via evaluation of the loss function to accommodate (1) and pruning and cross-validation is typically done for (2) [6]. In the setting with time-to-event data there are two splitting rules that are mostly adopted in growing survival trees: the log-rank splitting and log-rank score splitting. Precise details on the two splitting rules can be found in [6,11]. The growing process is terminated when the tree has grown to full size, i.e., when the terminating threshold has been met. The terminating threshold could be defined as, for example, a user pre-specified minimum observations per terminal node or when further splitting to daughter nodes is no better than mother node. When the tree has grown to full size, each terminal node within the survival tree is made up of a set of individuals that were ‘dropped down the tree’ via the same route and cumulative hazard estimates by Nelson- Aalen estimator may be obtained from each terminal nodes [12]. The final estimate of the cumulative hazard (CH) is thus an average measure of CH from all survival trees grown in the RSF.

Since the mechanisms with regard to the construction of the RSF is unknown, interpretability is thus burdensome. However, the RSF does output the variable importance measure (VIMP) which measures the increase (or decrease) in prediction error for the forest ensemble [5]. While the idea of VIMP has good empirical performance, it is informally defined and remained somewhat ad hoc. More recently, Ishwaran et al. [6] proposed the minimal depth (MD) measure which formalized the process of variable selection. Note that splitting and variable selection is traditionally done simultaneously, and it has been noted that such an approach is prone to overfitting and selection bias towards covariates with many possible splits [13]. Considering selection bias is important in survival tree construction because the biased selection would lead to the wrong summary measures such as VIMP and MD. Hothorn et al. [13] proposed a conditional Inference framework where they separated variable selection and splitting into a twostage procedure and has shown that such an approach has a better performance, especially when the data consists of covariates with many split-points. More recently, Wright et al. [14] had proposed using maximally selected rank statistics in order to have unbiased variable splitting. Intensive simulation studies on this issue has also been demonstrated by [14,15].

Application Involving Breast Cancer

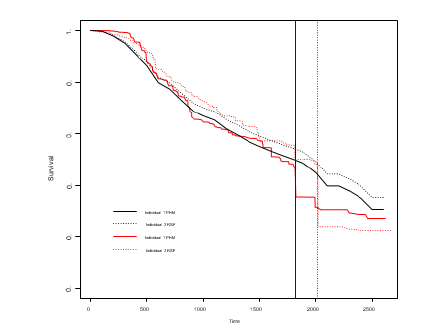
Figure 2:Predicted survival curves for two randomly chosen individuals with the blue lines indicating the true failure times; PHM = Proportional Hazards Model; RSF = Conditional Random Survival Forest.

We will give an illustrating example on the well-known German breast cancer study group 2 (GBSG2) dataset. Precise detail on the dataset can be found in Schumacher et al. [16].The dataset include 8 covariates as well as recurrence free survival time along with the event indicator. A propotional hazard model with no interactions has been fitted as our reference model and a conditional RSF with mtry = 3(splitting based on 3 randomly chosen covariates) and 600 trees has also been fitted as a comparison. We have checked the prediction error as a function of both mtry and the number of trees to the tune the RSF. Figure 2 shows the predicted survival curves as a function of time for 2 randomly chosen individuals who have been excluded from model construction. For visualization purposes, the blue lines represent the true failure times for the two individuals and we can see that RSF gives a lower estimated survival probability at the corresponding failure times. A more rigorous measure is needed of course in order to assess the predictive performance of the two methods and we have adopted the integrated Brier score [17]. A precise description on the formulation of the measure can be found in Houwelingen and Putter[17] The integrated Brier score for proportional hazard model and RSF over the course of 0 to maximum visit time have been estimated as 0.168 and 0.160 respectively under a fold cross-validation. From the results we can see that the RSF has a slightly better predictive performance compared to the proportional hazards model in the GBSG2 dataset.

Discussion

RSF is an attractive method when the goal is to do prediction. Its advantage is more apparent when the dimension of covariates is large, relationship between response and covariates are complex or when the proportional hazard assumption is at risk [8]. Although RSF acts as a great alternative in analyzing time-to-event data, it is worth nothing that interpretability is burdensome and that care must be taken when choosing and tunning the trees based on the form of available data.

References

• Jiang S, Cook R (2019) Score tests based on a finite mixture model of markov processes under intermittent observation. Statistics in Medicine 38: 3013-3025.
• Therneau T, Grambsch P (2000) Modeling survival data: second edition. Springer New York, USA.
• Cox D (1972) Regression models and life tables (with discussion). J R Stat Soc Ser B 34(2): 187-220.
• Friedman J, Hastie T, Tibshirini R (2008) The Elements of Statistical Learning: second edition. Springer New York, USA.
• Breiman L (2001) Random forests. Mach Learn 45: 5-32.
• Ishwaran H, Kogalur U, Blackstone E, Lauer M (2008) Random survival forests. The Annals of Applied Statistics 2(3): 841-860.
• Taylor J (2011) Random survival forests. Biostatistics for Clinicians 6(12): 1974-1975.
• Breiman L, Friedman J, Olshen R, Stone C (1984) Classification and Regression Trees. The Wadsworth Statistics/Probability Series, Wadsworth International Group, Belmont, CA.
• Breiman L (1996a) Bagging predictors. Mach Learn 26(2): 123-140.
• Breiman L (1996b) Heuristics of instability and stabilization in model selection. Ann Stat 24(6): 2350-2383.
• Segal M (1988) Regression trees for censored data. Biometrics 44(1): 45-47.
• Nelson W (1972) Theory and applications of hazard plotting for censored failure data. Technometrics 14(4): 945-965.
• Hothorn T, Hornik K, Zeileis A (2006) Unbiased recursive partitioning: A conditional inference framework. Journal of Computational and Graphical Statistics 15(3): 651-674.
• Wright M, Dankowski T, Ziegler A (2016) Unbiased split variable selection for random survival forests using maximally selected rank statistics. Statistics in Medicine 36: 1272-1284.
• Nasejje J, Mwambi HKD, Lesosky M (2017) A comparison of the conditional inference survival forest model to random survival forests based on a simulation study as well as on two applications with time-to-event data. BMC Medical Research Methodology 17: 115.
• Schumacher M, Basert G, Bojar H, Huebner K, Olschewski M, et al. (1994) Randomized 2 x 2 trial evaluating hormonal treatment and the duration of chemotherapy in node-positive breast cancer patients. German Breast Cancer Study Group. J Clin Oncol 12(10): 2086-2093.
• Hegarty P, Zheng Y (2005) Survival model predictive accuracy and ROC curves. Biometrics 61(1): 92-105.